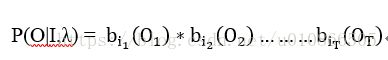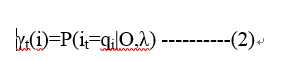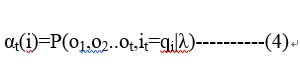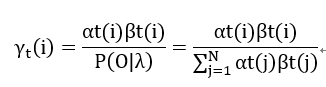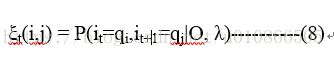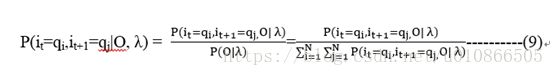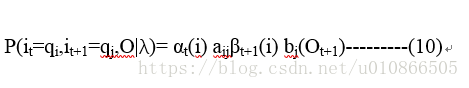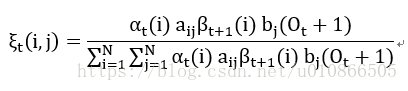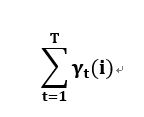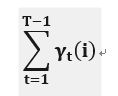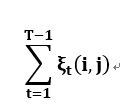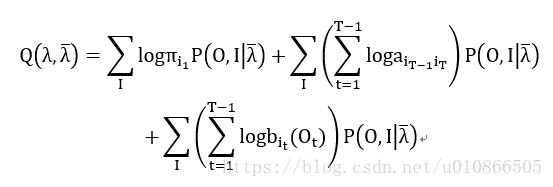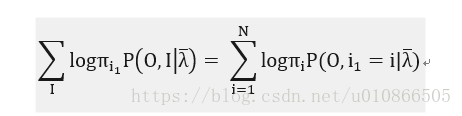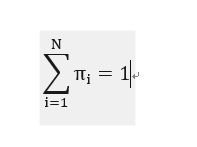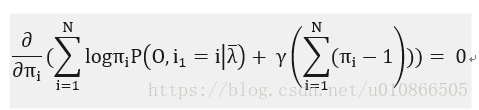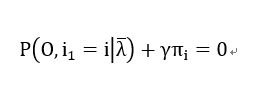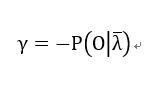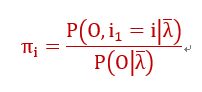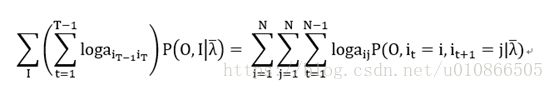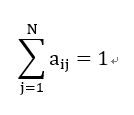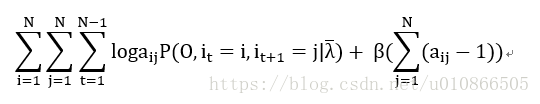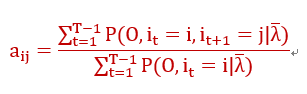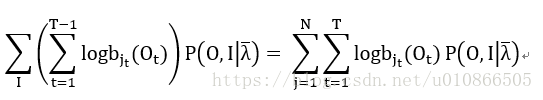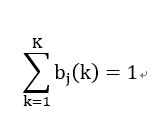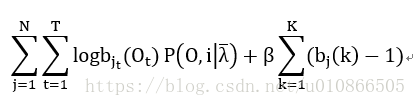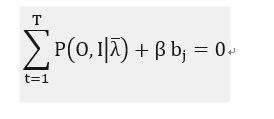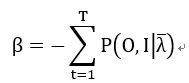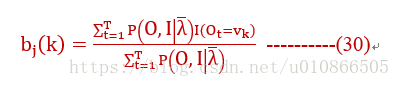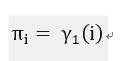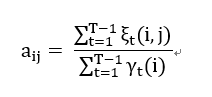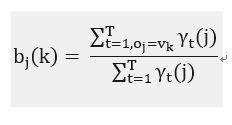HMM前向后向算法

HMM前向后向算法

HMM的三个基本问题中，对于HMM参数的学习是最难的。对于给定的观测序列O，如何估计模型参数使得P(O|λ)最大。目前为止，可能并不存在一种方法使得P(O|λ)最大，但是接下里的前向后向算法是能够使上述问题得到局部最优。

首先：假设给定模型λ和观测序列，计算观测序列出现的概率P(O|λ)。令隐含状态序列I={i₁,i₂...i_T};观测序列是O={O₁,O₂,...O_T},计算联合概率P(O,I|λ)，然后将所有可能的I进行求和，就是P(O|λ)。

隐含状态序列I的概率是:

当固定隐含状态I和给定模型参数时，观测序列为O={O₁,O₂,...O_T}的概率是P(O|I,λ)

O和I同时出现的概率是:

对所有的I进行求和:

---------(1)

(1)  式计算量太大，于是才有之前的前向算法和后向算法。

 

 

给定模型λ和观测序列O，在t时刻处于状态q_i的概率:

而且还有:

回顾一下：前向概率的定义:

给定HMM的参数λ，定义到t时刻的部分观测序列o₁,o₂..o_t，且状态是q_i的概率为前向概率:

后向概率的定义:

给定HMM的参数λ,在t时刻状态为q_i的条件下，t+1到T的观测序列o_t+1,o_t+2..o_T的概率为后向概率:

P(i_t=q_i,O|λ)的意思是:在给定HMM的参数λ，观测序列是O(O₁,O₂,...O_T),在t时刻的状态为q_i的概率。换句话理解就是:从1~t时刻，t时刻的状态为q_i,输出是(O₁,O₂,...O_t),的概率，然后t时刻之后，在t时刻状态为q_i，输出序列是(o_t+1,o_t+2..o_T)的概率。

1~t时刻的，输出是(O₁,O₂,...O_t),的概率:这不就是前向概率的定义么？

t时刻之后，在t时刻状态为q_i，输出序列是(o_t+1,o_t+2..o_T)的概率,这不就是后向概率么?

于是就有:

结合公式(1),(3),(6)，可以得到:

----------(7)

1.        

给定模型参数λ和观测序列O，t时刻是q_i，t+1时刻是q_j的概率是:

类似于公式(3)：

 

的意思是在给定HMM的参数下，观测序列是O，t时刻的状态是q_i，t+1时刻的状态是q_j的概率。

这个概率=P(1~t时刻的输出序列O₁,O₂,...O_t,t时刻是q_i|λ)*P(q_i转移到t+1时刻的q_j)*P(t+1时刻之后输出序列是o_t+2,o_t+3..o_T|t+1时刻是q_j, λ)*P(t+1时刻输出是O_t+1)：

这里面有好几个乘积，逐一解释：

P(1~t时刻的输出序列O₁,O₂,...O_t,t时刻是q_i|λ):这不就是t时刻的前向概率α_t(i)么？

P(q_i转移到t+1时刻的q_j):这不就是转移概率a_ij么？

P(t+1时刻之后输出序列是o_t+2,o_t+3..o_T|t+1时刻是q_j,λ):这不就是t+1时刻的后向概率β_t+1(i)么？

(注意:t+1时刻的后续输出序列是o_t+2,o_t+3..o_T,即下标是从t+2开始，不是t+1开始，请仔细理解后向概率的定义)。

前面少了O_t+1这个时间点的观测序列，因此要补上P(t+1时刻输出是O_t+1),而这个不就是b_j(O_t+1)么？

因此：

从而根据(8)，(9)，(10)可以变换为:

-----------(11)

---------(12)

(12)式表示观测序列是O时，状态i出现的期望

---------(13)

(13)式表示观测序列是O时，由状态i转移的期望

----------(14)

(14)式表示观测序列是O时，由状态i转移到j的期望.

 

2.       前向-后向算法(baum-welch)

这里主要来推导非监督情况下的baum-welch算法。

在只有观测序列时(只有O是已知的)，如何估计HMM的参数λ使得P(O|λ)最大，前面已经讲过了，由于没有办法找到一种方法使得P(O|λ)全局收敛，baum-welch算法只能是局部最优。

在公式(1)中有:

观测序列是O (o₁,o₂,...o_T)，隐含状态是I{i₁,i₂.....i_T},完全数据是(O,I)={ o₁,o₂,...o_T , i₁,i₂.....i_T}完全数据的对数似然函数是log(O,I|λ)。HMM的参数学习算法可以通过EM算法来实现。

E-step:

确定Q函数，即隐含变量的期望:

----------(16)

(不太懂这个公式是如何计算来的)

由于:

----------(17)

因此有:

----------(18)

M-step:

极大化来计算参数A,B,π。

对(18)式的三项分别进行极大化.

第一项:

其中:

于是，写成拉格朗日函数如下:

----------(19)

对(19)式求偏导:

----------(20)

于是可以计算出:

-----------(21)

同时求和可以得到:

----------(22)

将等式(22)带入到等式(21)中有:

----------(23)

等式(18)第二项:

-----------(24)

约束条件是:

同样让(24)变成拉格朗日函数式:

------------(25)

做法与第一项最大化一致，最后计算的结果是:

----------(26)

第三项:

-----------(27)

约束条件是:

类似的，构建拉格朗日函数:

----------(28)

对bj进行求偏导，并且令求偏导之后的函数为0,

----------(29)

对于(29)，如果t时刻，

同时对j求和，然后可以计算得到:

在时,(29)时左边才有意义，否则就是0，用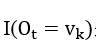来表示这种情况,于是可以计算b_j

以上(23),(26),(30)就是我们最终要的东西。

再进一步:

仔细看一下(23)和(7)，这俩不是一回事儿么？(23)分子不就是说在给定λ情况下，观测序列是O，在t时刻是i的概率么?于是有,只不过现在t=1而已:

----------(31)

同理:

----------(32)

----------(33)

至此，baum-welch算法就已经推导完成了。