【周赛总结】第32场双周赛,第201场周赛
2020/08/09 未参加
文章目录
- 第32场双周赛
- 1541.平衡括号字符串的最少括号数
- 1542.最长超赞回文串
- 第201场周赛
- 1544.整理字符串
- 1547 切棍子的最小成本
第32场双周赛
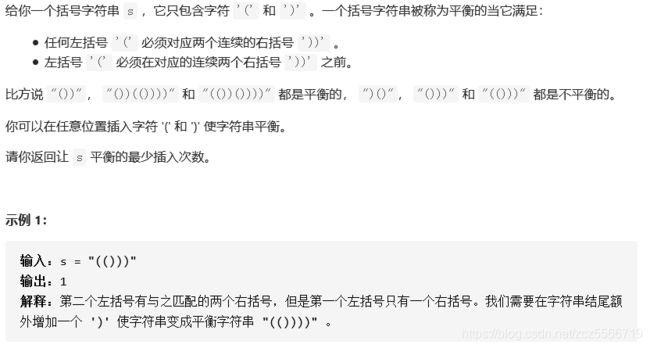
1541.平衡括号字符串的最少括号数
对于括号问题,似乎分情况讨论比较好。一般可以考虑维护两个变量,分别表示目前可使用的(和)的数量。这道题目有点偏方法。
class Solution {
public int minInsertions(String s) {
int left = 0, ans = 0, n = s.length();
for(int i = 0; i<n;i++){
// 分别考察现在是(还是)的情况。
if (s.charAt(i) == '(') left++;
else{
if (i+1<n && s.charAt(i+1) == ')') i++; // 寻找第二个)括号
else ans++; //否则添加第二个
if (left > 0) left--; // 前面已经满足了两个)),消除一个(
else ans++; // 添加一个(
}
}
// 如果最后有多的(
ans += left*2;
return ans;
}
}
1542.最长超赞回文串
题目的特点是子串,并且要找到最长子串。这个点很容易想到dp或者前缀和的方法。但是要求是回文串,回文串的点在于只能由最多一个奇数。并且我们需要考察前面的全部字符的个数。因此,这种考察多个字符的状态的问题,典型的方法就是状态压缩。
每次前缀和都是异或,并且我们子循环是每次考虑一个one hot的值。如果这个onehot可以与cur异或得到一个出现过的值,说明中间的某一段的异或和一定位onehot的,也就是满足以后一个奇数个。
如果cur是重复的,说明存在中间的某一段全部都是偶数的,也是符合的。
注意,初始要把0设置为-1.
class Solution {
public int longestAwesome(String s) {
//int[] dic = new int[10];
// 前缀和+状态压缩
// 为什么会想到使用状态压缩,因为我们每次要看好几个东西的存在状态。(并且,对于回文串,很强的01性)
int ans = 0, n = s.length(),cur = 0;
HashMap<Integer, Integer> dic = new HashMap<>();
dic.put(0, -1);
for (int i = 0;i<n;i++){
int key = s.charAt(i)-'0';
cur ^= 1<<key; //// 前缀和
for (int j = 0; j <10; j++){
int now = cur ^ (1<<j);
//// 如果出现过,说明有某一段的位的异或和是只有一个1的形式。
if (dic.containsKey(now)){
ans = Math.max(ans, i-dic.get(now));
}
}
if (!dic.containsKey(cur)) dic.put(cur,i);
else ans = Math.max(ans, i-dic.get(cur));
}
return ans;
}
}
第201场周赛
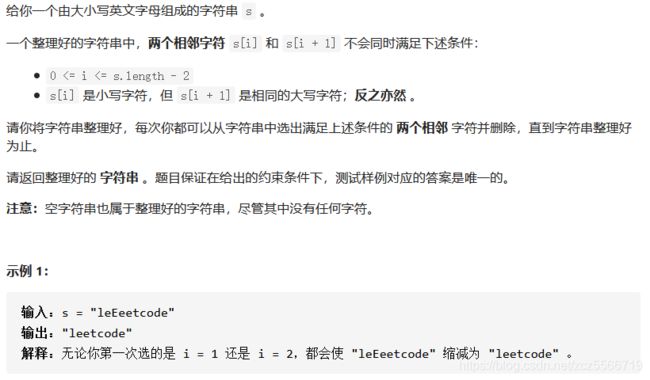
1544.整理字符串
关键还是练习Java的使用,这次有一个新的方法stack。
- 新建一个栈:
Stackstack = new Stack<>() - 进入栈:
stack.push(a); - 弹出栈顶:
stack.pop(); - 查询栈顶:
stack.peek() - 是否空栈:
stack.isEmpty()
class Solution {
public String makeGood(String s) {
if(s.length() == 0 || s.length() == 1) return s;
Stack<Character> stack = new Stack<>();
//遍历s
for(int i = 0; i < s.length(); i++){
char cur = s.charAt(i);
//若栈为空,则直接压栈即可
if(stack.isEmpty()){
stack.push(s.charAt(i));
continue;
}
//栈顶元素
char tmp = stack.peek();
if(cur-tmp == 32 || cur-tmp == -32){
stack.pop();
}else{
stack.push(cur);
}
}
StringBuilder res = new StringBuilder();
for (char j:stack){
res.append(j);
}
return res.toString();
}
}
1547 切棍子的最小成本
看到题目就是可以想到类似于扎气球的区间DP思路,但是这里还是没有分析清楚如何设计dp。
这里正确的方法应该是设计dp=[m+2][m+2],其中m是前面的cut的长度,前后补了两个边界。每次进行切割的代价其实就是区间的长度。
可以这么理解,dp[i][j]表示第i个切口和第j个切口之间的成本。
注意考虑一下初始的条件,dp[i][i+1]的表示只有其中一段,应该成本是0的。因为中间没有别的切口。
API:
Arrays.sort(list)对一个数组进行升序排序。Arrays.sort(a, Collections.reverseOrder());降序排列。Arrays.fill(int[], int)对一个行向进行填充
如果需要其他的排序方式,需要进行利用collections.sort并且重写compare方法:
Collections.sort(students, new Comparator<Student>() {
@Override
public int compare(Integer o1, Integer o2) {
// 返回一个正数,表示前面大于后面的,负数表示小于
// 如果调用compare方法大于0,就把前一个数和后一个数交换,也就是把大的数放后面了
/*
* 如果o1小于o2,我们就返回正值,如果o1大于o2我们就返回负值, 这样颠倒一下,就可以实现降序排序了,反之即可自定义升序排序了
*/
return o2 - o1;
});
class Solution {
public int minCost(int n, int[] cuts) {
// 首先需要进行排序,因为我们需要从后往前一次进行dp
Arrays.sort(cuts);
int m = cuts.length;
int[] p = new int[m+2];
p[0] = 0;
for (int i = 1; i<m+1; i++) p[i] = cuts[i-1];
p[m+1] = n;
int[][] dp = new int[m+2][m+2];
for (int i = 0; i<=m+1; i++){
Arrays.fill(dp[i], Integer.MAX_VALUE);
if(i<m+1) dp[i][i+1] = 0;
}
for (int i = m; i>=0; i--){ // 左端点
for (int j = i+1; j<=m+1;j++){ // 右端点
int cost = p[j]-p[i]; // 计算这一段切割的成本,正好等于长度
for(int k = i+1; k<j; k++){ // 分割点,一定得是中间的点
dp[i][j] = Math.min(dp[i][j], dp[i][k]+dp[k][j]+cost);
}
}
}
return dp[0][m+1];
}
}