索引
索引
知识大纲
- 索引的概念
- 索引的优缺点
- MySQL提供的索引类型
- MySQL的索引方法
- 索引的使用原则
1.索引的概念
索引:索引是对数据库表中一列或多列的值进行排序的一种结构。索引是一个单独的、物理的数据库结构,它是某个表中一列或若干列值的集合和相应的指向表中物理 标识这些值的数据页的逻辑指针清单。由此可知,索引是要消耗数据库空间的。而约束是一种逻辑概念。
例如:一本字典,如何快速找到某个字,可以给字典加目录,对数据库来说,索引的作 用即是给”数据”加目录。
设有 N 条随机记录,不用索引,平均查找 N/2 次,那么用了索引之后呢。如果是 btree(二叉树)索引,如果是 hash(哈希)索引,时间复杂度是 1。
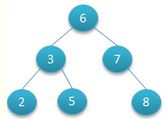
二叉查找树
二叉树具有以下性质:左子树的键值小于根的键值,右子树的键值大于根的键值。
如下图所示就是一棵二叉查找树
对该二叉树的节点进行查找发现深度为1的节点的查找次数为1,深度为2的查找次数为2,深度为n的节点的查找次数为n,因此其平均查找次数为 (1+2+2+3+3+3) / 6 = 2.3次
二叉查找树可以任意地构造,同样是2,3,5,6,7,8这六个数字,也可以按照下图的方式来构造:
但是这棵二叉树的查询效率就低了。因此若想二叉树的查询效率尽可能高,需要这棵二叉树是平衡的,从而引出新的定义——平衡二叉树,或称AVL树。
平衡二叉树(AVL Tree)
平衡二叉树(AVL树)在符合二叉查找树的条件下,还满足任何节点的两个子树的高度最大差为1。下面的两张图片,左边是AVL树,它的任何节点的两个子树的高度差<=1;右边的不是AVL树,其根节点的左子树高度为3,而右子树高度为1;
如果在AVL树中进行插入或删除节点,可能导致AVL树失去平衡,这种失去平衡的二叉树可以概括为四种姿态:LL(左左)、LR(左右)、RL(右左)、RR(右右)。它们的示意图如下:
这四种失去平衡的姿态都有各自的定义:
LL:LeftLeft,也称“左左”。插入或删除一个节点后,根节点的左孩子(Left Child)的左孩子(Left Child)还有非空节点,导致根节点的左子树高度比右子树高度高2,AVL树失去平衡。
RR:RightRight,也称“右右”。插入或删除一个节点后,根节点的右孩子(Right Child)的右孩子(Right Child)还有非空节点,导致根节点的右子树高度比左子树高度高2,AVL树失去平衡。
LR:LeftRight,也称“左右”。插入或删除一个节点后,根节点的左孩子(Left Child)的右孩子(Right Child)还有非空节点,导致根节点的左子树高度比右子树高度高2,AVL树失去平衡。
RL:RightLeft,也称“右左”。插入或删除一个节点后,根节点的右孩子(Right Child)的左孩子(Left Child)还有非空节点,导致根节点的右子树高度比左子树高度高2,AVL树失去平衡。
BTree特性
InnoDB存储引擎中默认每个页的大小为16KB,InnoDB在把磁盘数据读入到磁盘时会以页为基本单位,B-Tree结构的数据可以让系统高效的找到数据所在的磁盘块。为了描述B-Tree,首先定义一条记录为一个二元组[key, data] ,key为记录的键值,对应表中的主键值,data为一行记录中除主键外的数据。对于不同的记录,key值互不相同。
模拟查找关键字29的过程:
\1. 根据根节点找到磁盘块1,读入内存。【磁盘I/O操作第1次】
\2. 比较关键字29在区间(17,35),找到磁盘块1的指针P2。
\3. 根据P2指针找到磁盘块3,读入内存。【磁盘I/O操作第2次】
\4. 比较关键字29在区间(26,30),找到磁盘块3的指针P2。
\5. 根据P2指针找到磁盘块8,读入内存。【磁盘I/O操作第3次】
\6. 在磁盘块8中的关键字列表中找到关键字29。
分析上面过程,发现需要3次磁盘I/O操作,和3次内存查找操作。由于内存中的关键字是一个有序表结构,可以利用二分法查找提高效率。而3次磁盘I/O操作是影响整个B-Tree查找效率的决定因素。B-Tree相对于AVLTree缩减了节点个数,使每次磁盘I/O取到内存的数据都发挥了作用,从而提高了查询效率。
B树上大部分的操作(插入、删除、查询)所需要的磁盘存取次数和B树的高度是成正比的,并且B树是尽量多的在节点上存储信息,保证导数尽量少,在B树中可以检查多个子结点,由于在一棵树中检查任意一个结点都需要一次磁盘访问,所以B树避免了大量的磁盘访问,减少了磁盘I/O。
2.索引的优缺点
索引好处:加快了查询速度(select )
索引坏处:降低了增,删,改的速度(update/delete/insert),增大了表的文件大小(索引文件 甚至可能比数据文件还大)
3.MySQL 提供多种索引类型:
- 普通索引
- 唯一性索引
- 主键索引:只有一个主键索引
- 全文索引:X 版本只有MyISAM存储引擎支持FULLTEXT,并且只限于 CHAR、VARCHAR和 TEXT 类型的列上创建。
4.MySQL 的索引方法:
- HASH
- B-TREE
- MySQL 中多数索引都以 BTREE 的形式保存。
5.索引的使用原则:
(1)不过度索引
(2)索引条件列(where 后面最频繁的条件比较适宜索引)
(3)索引散列值,过于集中的值不要索引,例如:给性别”男”,”女”加索引,意义不大
CREATE INDEX 索引名 ON 表名称 (column_name,[column_name…]); 最左边的列最关键
alter table 表名称 drop index 索引名;