Dijkstra 算法【C实现】

迪杰斯特拉算法是求解图中一个节点到其余所有节点的权重和最小时的最小路径，并可通过某种方式显示出来.

如图所示，算法应可以实现求出图中任一节点到其余节点的最短路径才可以,比如说2到0最短路为0——1——2,同时需注意本程序需支持C99特性，Gcc是完全可以的，别的编译器啥的就不知道了,运行实例如下：

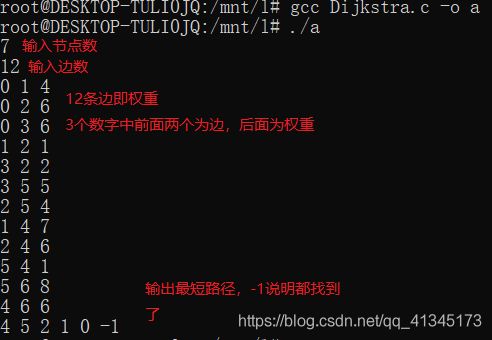
//需求：用户只需输入图中节点数目，有效边的个数及边上权重，该程序可给出最短路径
#include
#include
#define INF 65535  //定义为权重无穷大
typedef struct {   //图邻接矩阵表示法
	int Vnum;
	int **T;   //邻接矩阵
}Graph;
typedef Graph *PGraph;
PGraph create_graph()//动态创建并分配内存空间
{
	int n;
	PGraph G =(PGraph)malloc(sizeof(Graph));
	scanf("%d",&G->Vnum);
	n = G->Vnum;
	G->T = (int **)malloc(n*sizeof(int *));
	for(int i=0;i<n;++i)
	{
		G->T[i]=(int *)malloc(sizeof(int)*n);
		for(int j=0;j<n;++j)
		{
			if(i==j)
				G->T[i][j] = 0;
			else
				G->T[i][j] =INF;
		}
	}
	return G;
}
int Dijkstra(int n,int **Graph,int v0,int *dist,int *path) //迪杰斯特拉算法核心要点
{
	int set[n];
	for(int i=0;i<n;++i)
	{
		dist[i] = Graph[v0][i];
		set[i] = 0;
		if(Graph[v0][i]<INF)
			path[i] = v0;
		else
			path[i] =-1;
	}
	path[v0] = -1;
	set[v0]=1;
	int min , v;
	for(int i=0;i<n;++i)
	{	
		min = INF;
		for(int j=0;j<n;j++)
		{
			if(set[j]!=1&&dist[j]<min)
			{
				min = dist[j];
				v = j;
			}
		}
		set[v] = 1;
		for(int j=0;j<n;++j)
		if(set[j]==0&&dist[v]+Graph[v][j]<dist[j])
		{
			dist[j] = dist[v]+Graph[v][j];
			path[j] = v;
		}
	}
	return 0;
}
void Getpath(int *path , int n) //依据所给节点打印出最短路径
{
	int x = path[n];
	printf("%d ",x);
	while(x!=-1)
	{
		x=path[x];
		printf("%d ",x);
	}
	printf("\n");
}
int main(void)
{
	PGraph G;
	int  a,b,w;
	int e;
	G = create_graph();
	scanf("%d",&e);
	for(int i=0;i<e;++i)
	{
	scanf("%d %d %d",&a,&b,&w);
	G->T[a][b] = w;
	}
	int dist[G->Vnum];
	int path[G->Vnum];
	Dijkstra(G->Vnum,G->T,0,dist,path);
	Getpath(path ,6);
	free(G->T);
	free(G);
	return 0;
}

Floyd求图中所有任意两节点之间的最短距离，并打印出来

void Floyd(int n,int **G,int path[][n]) //Floyd算法核心要点
{
	int A[n][n];
	for(int i=0;i<n;++i)
	{
		for(int j=0;j<n;++j)
		{
			A[i][j] = G[i][j];
			path[i][j] = -1;
		}
	}
	for(int i=0;i<n;++i)
	{
		for(int j=0;j<n;++j)
			for(int k=0;k<n;++k)
				if(i!=k&&j!=k&&A[i][j]>A[i][k]+A[k][j])
				{
					A[i][j] = A[i][k]+A[k][j];
					path[i][j] = k;
				}
	}
}
void Getpath(int n,int (*path)[n] , int u,int v) //依据所给一对节点打印出最短路径
{
	if(path[u][v]==-1)
		printf("%d ",v);
	else
	{
		int mid = path[u][v];
		Getpath(n,path,u,mid);
		Getpath(n,path,mid,v);
	}
}