链式表示的栈——链式栈4——算术表达式

通过键盘输入一个表达式，如21-(15+7*9)/3,要求将其转换为后缀表达式，并计算表达式的值。

【分析】求表达式的值是高级程序设计语言中编译器设计的一个基本问题。它的实现借助于栈的“后进先出”特性。
一个算术表达式是由操作数（运算对象）、运算符和分解符（括号）组成的有意义的式子。运算符从运算对象的个数上分为单目运算符和双目运算符；从运算类型上可以分为算术运算符、关系运算符、逻辑运算符等，在此为了简化问题考虑，我们假设算术运算符只包含加，减，乘，除双目运算符和左右两种圆括号。例如：
a-(b+c*d)/e

这种算术表达式中的运算符总出现在两个操作数之间，这种算术表达式称为中缀表达式。计算机编译系统在计算一个算术表达式之前要将中缀表达式转换为后缀表达式，然后对后缀表达式进行计算。后缀表达式就是算术运算符出现在操作数之后，并且不含括号。在计算机中求解算术表达式的值分为两个步骤：
（1）将中缀表达式转换为后缀表达式
（2）依据后缀表达式计算表达式的值

1.将中缀表达式转换为后缀表达式

要将一个中缀表达式转换为后缀表达式，首先要了解算术四则运算的规则。算术的四则运算的规则是：
（1）算术表达式的优先级：先乘除，后加减；
（2）有括号的先算括号里的，后算括号外的，多层括号的由内到外进行；
（3）同级别的从左到右进行计算；

上面的算术表达式转换为后缀表达式为：

a b c d * + e / -

不难看出后缀表达式具有以下3个特点：

（1）后缀表达式与中缀表达式的操作数出现顺序相同，只是运算符先后顺序改变了；
（2）后缀表达式不出现括号；
（3）后缀表达式的操作符出现在操作数之后。

后缀表达式也叫作逆波兰表达式，是波兰逻辑学家Jan.Lukasiewicz于1929年提出的表示方法。每个运算符都位于操作数之后，故称为后缀表示。后缀表达式既无括号也无优先级的约束，因此只需要从左到右依次扫描后缀表达式的各个字符，遇到运算符时，直接对运算符前面两个操作数进行运算即可。

如何将中缀表达式转换为后缀表达式呢？可以设置一个栈，用于存放运算符。依次读入表达式中的每个字符，如果是操作数直接输出。如果是运算符，则比较栈顶元素符与当前运算符的优先级，然后进行处理，直到整个表达式处理完毕。我们约定‘#’作为后缀表达式的结束标志，假设θ1为栈运算符，θ2为当前扫描的运算符。则中缀表达式转换为后缀表达式的算法描述如下：
（1）初始化栈，并将‘#’入栈；
（2）若当前字符是操作数，则将该操作数输出，并读入下一字符；
（3）若当前字符是运算符，记作θ2，将θ2与栈顶的运算符θ1比较。若θ1优先级低于θ2，则将θ2进栈；若θ1优先级高于θ2，则将θ1出栈并将其作为后缀表达式输出。然后继续比较新的栈顶运算符θ1和与当前运算符θ2的优先级，若θ1的优先级与θ2相等，且θ1为‘(’,θ2为‘)’,则将θ1出栈，继续读入下一个字符；
（4）如果θ2的优先级与θ1相等，且θ1和θ2都为‘#’，将θ1出栈，栈为空。则完成中缀表达式转换为后缀表达式，算法结束。
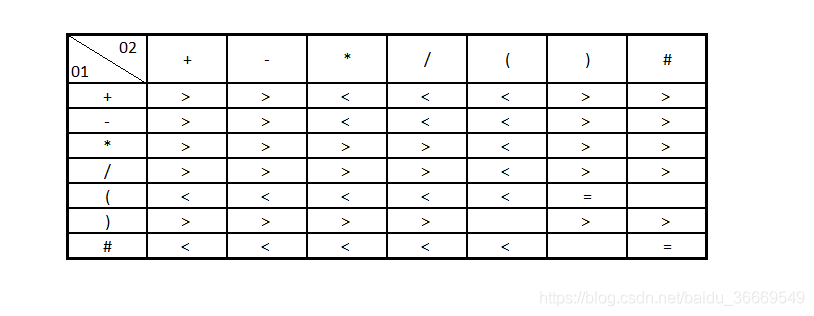
运算符的优先级关系如表所示：

利用上述算法，将中缀表达式a-(b+c*d)/e转换为后缀表达式的输出过程如下表（为了便与描述，在表达式末尾加一个结束标志‘#’）
 

2.后缀表达式的计算

在计算后缀表达式时，需要设置两个栈：operator栈和openand栈。其中operator栈用于存放运算符，operand用于存放操作数和中间运算结果。具体运算思想如下：依次读入后缀表达式中的每个字符，如果是操作数，则将操作数进入operand栈。如果是运算符，则将操作数出栈两次，然后对操作数进行当前操作符的运算。直到整个表达式处理完毕。
LinkStack.h

#pragma once
#include 
#include 

using namespace std;
typedef char DataType;
typedef struct node 
{
	DataType data;
	struct node *next;
}LStackNode,*LinkStack;


void InitStack(LinkStack *top)
{
	if ((*top=(LinkStack)malloc(sizeof(LStackNode)))==NULL)
	{
		exit(-1);
	}
	(*top)->next = NULL;
}

int StackEmpty(LinkStack top)
{
	if (top->next==NULL)
	{
		return 1;
	}
	else
	{
		return 0;
	}
}

int PushStack(LinkStack top, DataType e)
{
	LStackNode *p;
	if ((p=(LStackNode*)malloc(sizeof(LStackNode)))==NULL)
	{
		cout << "内存分配失败！";
		exit(-1);
	}
	p->data = e;
	p->next = top->next;
	top->next = p;
	return 1;
}

int PopStack(LinkStack top, DataType *e)
{
	LStackNode *p;
	p = top->next;
	if (!p)
	{
		cout << "栈已空！";
		return 0;
	}
	top->next = p->next;
	*e = p->data;
	free(p);
	return 1;
}

int GetTop(LinkStack top, DataType *e)

{
	LStackNode *p;
	p = top->next;
	if (!p)
	{
		cout << "栈已空！";
		return 0;
	}

	*e = p->data;
	return 1;
}

int StackLength(LinkStack top)
{
	LStackNode *p;
	int count = 0;
	p = top;
	while (p->next!=NULL)
	{
		p = p->next;
		count++;

	}
	return count;
}

void DestoryStack(LinkStack top)
{
	LStackNode *p, *q;
	p = top;
	while (!p)
	{
		q = p;
		p = p->next;
		free(q);

	}
}

main.cpp

#include 
#include 
#include 
#include 
#include "LinkStack.h"
#define MAXSIZE 50
typedef struct
{
	float data[MAXSIZE];
	int top;
}OpStack;
void TranslateExpress(char s1[],char s2[]);
float ComputeExpress(char s[]);
void main()
{
	char a[MAXSIZE], b[MAXSIZE];
	float f;
	cout << "请输入一个算术表达式：" << endl;
	gets_s(a);
	cout << "中缀表达式为：" << a;
	TranslateExpress(a,b);
	cout << "后缀表达式为：" << b << endl;
	f = ComputeExpress(b);
	cout << "计算结果：" << f << endl;

	system("pause");
}
float ComputeExpress(char a[])
{
	OpStack S;
	int i = 0, value;
	float x1, x2;
	float result;
	S.top = -1;
	while (a[i]!='\0')
	{
		if (a[i]!=' '&&a[i]>='0'&&a[i]<='9')
		{
			value = 0;
			while (a[i]!=' ')
			{
				value = 10 * value + a[i] - '0';
				i++;

			}
			S.top++;
			S.data[S.top] = value;
		}
		else
		{
			switch (a[i])
			{
			case '+':
				x1 = S.data[S.top];
				S.top--;
				x2 = S.data[S.top];
				S.top--;
				result = x1 + x2;
				S.top++;
				S.data[S.top] = result;
				break;
			case '-':
				x1 = S.data[S.top];
				S.top--;
				x2 = S.data[S.top];
				S.top--;
				result = x2 - x1;
				S.top++;
				S.data[S.top] = result;
				break;
			case '*':
				x1 = S.data[S.top];
				S.top--;
				x2 = S.data[S.top];
				S.top--;
				result = x1*x2;
				S.top++;
				S.data[S.top] = result;
				break;
			case '/':
				x1 = S.data[S.top];
				S.top--;
				x2 = S.data[S.top];
				S.top--;
				result = x2 / x1;
				S.top++;
				S.data[S.top] = result;
				break;
			//default:
			//	break;
			}
			i++;
		}
	}

	if (!S.top!=-1)
	{
		result = S.data[S.top];
		S.top--;
		if (S.top==-1)
		{
			return result;
		}
		else
		{
			cout << "表达式错误！";
			exit(-1);
		}
	}
}

void TranslateExpress(char str[], char exp[])
{
	LinkStack S;
	char ch;
	DataType e;
	int i = 0, j = 0;
	InitStack(&S);
	ch = str[i];
	i++;
	while (ch!='\0')
	{
		switch (ch)
		{
		case '(':
			PushStack(S, ch);
			break;
		case ')':
			while (GetTop(S,&e)&&e!='(')
			{
				PopStack(S, &e);
				exp[j] = e;
				j++;
				exp[j] = ' ';
				j++;
			}
			PopStack(S, &e);
			break;
		case '+':
		case '-':
			while (!StackEmpty(S)&&GetTop(S,&e)&&e!='(')
			{
				PopStack(S, &e);
				exp[j] = e;
				j++;
				exp[j] = ' ';
				j++;

			}
			PushStack(S, ch);
			break;
		case '*':
		case '/':
			while (!StackEmpty(S)&&GetTop(S,&e)&&e=='/'||e=='*')
			{
				PopStack(S, &e);
				exp[j] = e;
				j++;
				exp[j] = ' ';
				j++;
			}
			PushStack(S, ch);
			break;

		default:
			while (ch>='0'&&ch<='9')
			{
				exp[j] = ch;
				j++;
				ch = str[i];
				i++;
			}
			i--;
			exp[j] = ' ';
			j++;
			/*break;*/
		}

		ch = str[i];
		i++;
	}
	while (!StackEmpty(S))
	{
		PopStack(S, &e);
		exp[j] = e;
		j++;
		exp[j] = ' ';
		j ++;
	}

	exp[j] = '\0';

}

结果：