布隆过滤器(BloomFilter)原理 实现和性能测试

布隆过滤器(BloomFilter)是一种大家在学校没怎么学过，但在计算机很多领域非常常用的数据结构，它可以用来高效判断某个key是否属于一个集合，有极高的插入和查询效率(O(1))，也非常省存储空间。当然它也不是完美无缺，它也有自己的缺点，接下来跟随我一起详细了解下BloomFilter的实现原理，以及它优缺点、应用场景，最后再看下Google guava包中BloomFilter的实现，并对比下它和HashSet在不同数据量下内存空间的使用情况。

学过数据结构的人都知道，在计算机领域我们经常通过牺牲空间换时间，或者牺牲时间换空间，BloomFilter给了我们一种新的思路——牺牲准确率换空间。是的，BloomFilter不是100%准确的，它是有可能有误判，但绝对不会有漏判断，说通俗点就是，BloomFilter有可能错杀好人，但不会放过任何一个坏人。BloomFilter最大的优点就是省空间，缺点就是不是100%准确，这点当然和它的实现原理有关。

BloomFilter的原理

在讲解BloomFilter的实现前，我们先来了解下什么叫Bitmap(位图)，先给你一道《编程珠玑》上的题目。

给你一个有100w个数的集合S，每个数的数据大小都是0-100w，有些数据重复出现，这就意味着有些数据可能都没出现过，让你以O(n)的时间复杂度找出0-100w之间没有出现在S中的数，尽可能减少内存的使用。

既然时间复杂度都限制是O(N)了，意味着我们不能使用排序了，我们可以开一个长为100w的int数组来标记下哪些数字出现过，在就标1，不在标0。但对于每个数来说我们只需要知道它在不在，只是0和1的区别，用int(32位)有点太浪费空间了，我们可以按二进制位来用每个int，这样一个int就可以标记32个数，空间占用率一下子减少到原来的1/32，于是我们就有了位图，Bitmap就是用n个二进制位来记录0-m之间的某个数有没有出现过。

Bitmap的局限在于它的存储数据类型有限，只能存0-m之间的数，其他的数据就存不了了。如果我们想存字符串或者其他数据怎么办？其实也简单，只需要实现一个hash函数，将你要存的数据映射到0-m之间就行了。这里假设你的hash函数产生的映射值是均匀的，我们来计算下一个m位的Bitmap到底能存多少数据?
当你在Bitmap中插入了一个数后，通过hash函数计算它在Bitmap中的位置并将其置为1，这时任意一个位置没有被标为1的概率是：

$$1-\frac{1}{m}$$
当插入n个数后，这个概率会变成：
$$(1-\frac{1}{m}{)}^n$$
所以任意一个位置被标记成1的概率就是：
$$P_1=1-(1-\frac{1}{m}{)}^n$$
这时候你判断某个key是否在这个集合S中时，只需要看下这个key在hash在Bitmap上对应的位置是否为1就行了，因为两个key对应的hash值可能是一样的，所以有可能会误判，你之前插入了a，但是hash(b)==hash(a)，这时候你判断b是否在集合S中时，看到的是a的结果，实际上b没有插入过。

从上面公式中可以看出有 $P_1$ 的概率可能会误判，尤其当n比较大时这个误判概率还是挺大的。 如何减少这个误判率？我们最开始是只取了一个hash函数，如果说取k个不同的hash函数呢！我们每插入一个数据，计算k个hash值，并对k位置为1。在查找时，也是求k个hash值，然后看其是否都为1，如果都为1肯定就可以认为这个数是在集合S中的。
问题来了，用k个hash函数，每次插入都可能会写k位，更耗空间，那在同样的m下，误判率是否会更高呢？我们来推导下。

在k个hash函数的情况下，插入一个数后任意一个位置依旧是0的概率是：
$$(1-\frac{1}{m}{)}^k$$
插入n个数后任意一个位置依旧是0的概率是：
$$(1-\frac{1}{m}{)}^{kn}$$
所以可知，插入n个数后任意一个位置是1的概率是

$$1-(1-\frac{1}{m}{)}^{kn}$$
因为我们用是用k个hash共同来判断是否是在集合中的，可知当用k个hash函数时其误判率如下。它一定是比上面1个hash函数时误判率要小（虽然我不会证明）
$${\left(1-{\left[1-\frac{1}{m}\right]}^{kn}\right)}^k<(1-{\left[1-\frac{1}{m}\right]}^n)$$
维基百科也给出了这个误判率的近似公式（虽然我不知道是怎么来的，所以这里就直接引用了）
$${\left(1-{\left[1-\frac{1}{m}\right]}^{kn}\right)}^k\approx {\left(1-e^{-kn/m}\right)}^k$$

到这里，我们重新发明了Bloomfilter，就是这么简单，说白了Bloomfilter就是在Bitmap之上的扩展而已。对于一个key，用k个hash函数映射到Bitmap上，查找时只需要对要查找的内容同样做k次hash映射，通过查看Bitmap上这k个位置是否都被标记了来判断是否之前被插入过，如下图。

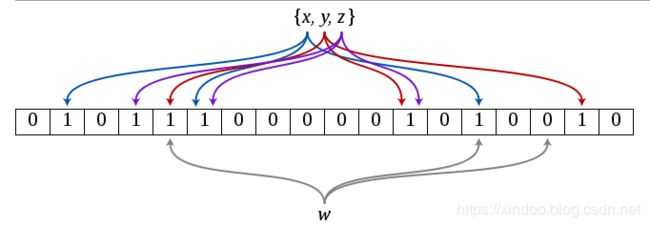
通过公式推导和了解原理后，我们已经知道Bloomfilter有个很大的缺点就是不是100%准确，有误判的可能性。但是通过选取合适的bitmap大小和hash函数个数后，我们可以把误判率降到很低，在大数据盛行的时代，适当牺牲准确率来减少存储消耗还是很值得的。

除了误判之外，BloomFilter还有另外一个很大的缺点 只支持插入，无法做删除。如果你想在Bloomfilter中删除某个key，你不能直接将其对应的k个位全部置为0，因为这些位置有可能是被其他key共享的。基于这个缺点也有一些支持删除的BloomFilter的变种，适当牺牲了空间效率，感兴趣可以自行搜索下。

如何确定最优的m和k？

知道原理后再来了解下怎么去实现，我们在决定使用Bloomfilter之前，需要知道两个数据，一个是要存储的数量n和预期的误判率p。bitmap的大小m决定了存储空间的大小，hash函数个数k决定了计算量的大小，我们当然都希望m和k都越小越好，如何计算二者的最优值，我们大概来推导下。（备注：推导过程来自Wikipedia）

由上文可知，误判率p为
$$p\approx {\left(1-e^{-kn/m}\right)}^k(1)$$
对于给定的m和n我们想让误判率p最小，就得让
$$k=\frac{m}{n}\ln 2(2)$$
把(2)式代入(1)中可得
$$p={\left(1-e^{-\left(\frac{m}{n}\ln 2\right)\frac{n}{m}}\right)}^{\frac{m}{n}\ln 2}(3)$$
对(3)两边同时取ln并简化后，得到
$$\ln p=-\frac{m}{n}(\ln 2{)}^2$$
最后可以计算出m的最优值为
$$m=-\frac{n\ln p}{(\ln 2{)}^2}$$
因为误判率p和要插入的数据量n是已知的，所以我们可以直接根据上式计算出m的值，然后把m和n的值代回到(2)式中就可以得到k的值。至此我们就知道了实现一个bloomfilter所需要的所有参数了，接下来让我们看下Google guava包中是如何实现BloomFilter的。

guava中的BloomFilter

BloomFilter无法通过new去创建新对象，而它提供了create静态方法来生成对象，其核心方法如下。

  static <T> BloomFilter<T> create(
      Funnel<? super T> funnel, long expectedInsertions, double fpp, Strategy strategy) {
    checkNotNull(funnel);
    checkArgument(
        expectedInsertions >= 0, "Expected insertions (%s) must be >= 0", expectedInsertions);
    checkArgument(fpp > 0.0, "False positive probability (%s) must be > 0.0", fpp);
    checkArgument(fpp < 1.0, "False positive probability (%s) must be < 1.0", fpp);
    checkNotNull(strategy);

    if (expectedInsertions == 0) {
      expectedInsertions = 1;
    }

    long numBits = optimalNumOfBits(expectedInsertions, fpp);
    int numHashFunctions = optimalNumOfHashFunctions(expectedInsertions, numBits);
    try {
      return new BloomFilter<T>(new LockFreeBitArray(numBits), numHashFunctions, funnel, strategy);
    } catch (IllegalArgumentException e) {
      throw new IllegalArgumentException("Could not create BloomFilter of " + numBits + " bits", e);
    }
  }

从代码可以看出，需要4个参数，分别是

• funnel 用来对参数做转化,方便生成hash值
• expectedInsertions 预期插入的数据量大小，也就是上文公式中的n
• fpp 误判率，也就是上文公式中的误判率p
• strategy 生成hash值的策略，guava中也提供了默认策略，一般不需要你自己重新实现

从上面代码可知，BloomFilter创建过程中先检查参数的合法性，之后使用n和p来计算bitmap的大小m（optimalNumOfBits(expectedInsertions, fpp)），通过n和m计算hash函数的个数k（optimalNumOfHashFunctions(expectedInsertions, numBits)）,这俩方法的具体实现如下。

  static int optimalNumOfHashFunctions(long n, long m) {
    // (m / n) * log(2), but avoid truncation due to division!
    return Math.max(1, (int) Math.round((double) m / n * Math.log(2)));
  }
  static long optimalNumOfBits(long n, double p) {
    if (p == 0) {
      p = Double.MIN_VALUE;
    }
    return (long) (-n * Math.log(p) / (Math.log(2) * Math.log(2)));
  }

其实就是上文中列出的计算公式。
后面插入和查找的逻辑就比较简单了，这里不再赘述，有兴趣可以看下源码，我们这里通过BloomFilter提供的方法列表了解下它的功能就行。

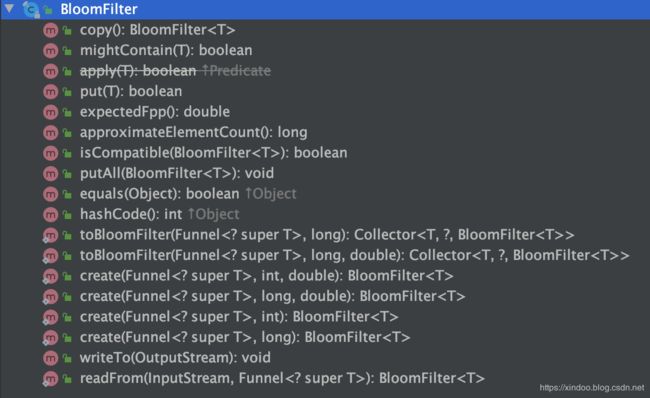
从上图可以看出，BloomFilter除了提供创建和几个核心的功能外，还支持写入Stream或从Stream中重新生成BloomFilter，方便数据的共享和传输。

使用案例

• HBase、BigTable、Cassandra、PostgreSQ等著名开源项目都用BloomFilter来减少对磁盘的访问次数，提升性能。
• Chrome浏览器用BloomFilter来判别恶意网站。
• 爬虫用BloomFilter来判断某个url是否爬取过。
• 比特币也用到了BloomFilter来加速钱包信息的同步。
  ……

和HashSet对比

我们一直在说BloomFilter有巨大的存储优势，做个优势到底有多明显，我们拿jdk自带的HashSet和guava中实现的BloomFilter做下对比，数据仅供参考。

测试环境

测试平台 Mac
guava(28.1)BloomFilter，JDK11(64位) HashSet
使用om.carrotsearch.java-sizeof计算实际占用的内存空间

测试方式

BloomFilter vs HashSet

分别往BloomFilter和HashSet中插入UUID，总计插入100w个UUID，BloomFilter误判率为默认值0.03。每插入5w个统计下各自的占用空间。结果如下，横轴是数据量大小，纵轴是存储空间，单位kb。

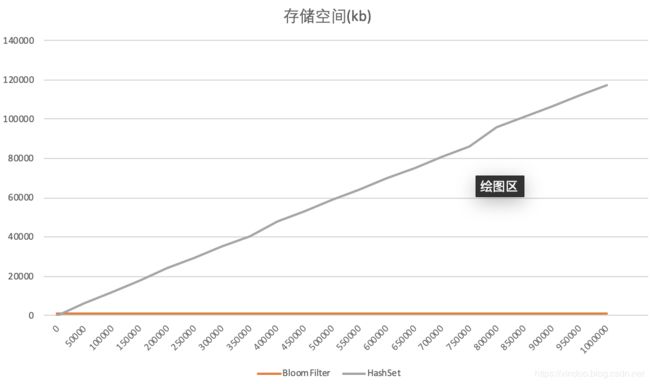
可以看到BloomFilter存储空间一直都没有变，这里和它的实现有关，事实上你在告诉它总共要插入多少条数据时BloomFilter就计算并申请好了内存空间，所以BloomFilter占用内存不会随插入数据的多少而变化。相反，HashSet在插入数据越来越多时，其占用的内存空间也会越来越多，最终在插入完100w条数据后，其内存占用为BloomFilter的100多倍。

在不同fpp下的存储表现

在不同的误判率下，插入100w个UUID，计算其内存空间占用。结果如下，横轴是误判率大小，纵轴是存储空间，单位kb。

fpp,size
0.1,585.453125
0.01,1170.4765625
1.0E-3,1755.5
1.0E-4,2340.53125
1.0E-5,2925.5546875
1.0E-6,3510.578125
1.0E-7,4095.6015625
1.0E-8,4680.6328125
1.0E-9,5265.65625
1.0E-10,5850.6796875

可以看出，在同等数据量的情况下，BloomFilter的存储空间和ln(fpp)呈反比，所以增长速率其实不算快，即便误判率减少9个量级，其存储空间也只是增加了10倍。

参考资料

1. wikipedia bloom filter