小白专场： File Transfer--集合的简化表示，按秩归并与路径压缩

集合的简化表示

原始的集合表示：

typedef struct {
ElementType Data;
int Parent;
} SetType;

int Find(SetType S[], Elemtype X)
{	//在数组S中查找值为X的元素所属的集合
	//MaxSize是全局变量，为数组S的最大长度
	int i;
	for (i = 0; i < MaxSize && S[i].Data != X; i++);
	if (i >= MaxSize) return -1; //未找到X，返回-1
	for (; S[i].Parent >= 0; i = S[i].Parent);
	return i;//找到X所属集合，返回树根结点在数组S中的下标
}

集合的简化表示：

任何有限集合的（N个）元素都可以被一一映射为整数0 ~ N–1

集合中元素在树结构中的排列没有顺序，所以可以用下标代替代替该元素，每一个下标对应一个元素，形成一种一一对应的关系

typedef int ElementType; /*默认元素可以用非负整数表示*/
typedef int SetName; 	/*默认用根结点的下标作为集合名称*/
typedef ElementType SetType[MaxSize];
SetName Find(SetType S, ElementType X)
{ /* 默认集合元素全部初始化为-1 */
	for (; S[X] >= 0; X = S[X]);
	return X;
}
void Union(SetType S, SetName Root1, SetName Root2)
{ /* 这里默认Root1和Root2是不同集合的根结点*/
	S[Root2] = Root1;
}

题目：

第一行，表示集合中有几个元素
C 3 2：检查3和2是否属于同一集合
I 3 2：将3和2所在集合合并
S：程序结束，如果只存在一个集合，输出：The network is connected.如果有n个集合，输出：There are %d components.

程序框架搭建

int main()
{
	初始化集合;
	do {
		读入一条指令;
		处理指令;
	} while (没结束);
	return 0;
}

int main()
{
	SetType S;
	int n;
	char in;
	cin>>n;
	Initialization(S, n);//每一个元素都是一个集合，全部初始化为-1
	do {
		cin>>in;
		switch (in) {
		case 'I': Input_connection(S); break;
		case 'C': Check_connection(S); break;
		case 'S': Check_network(S, n); break;
		}
	} while (in != 'S');
	return 0;
}
//将两个元素所在集合合并
void Input_connection(SetType S)
{
	ElementType u, v;
	SetName Root1, Root2;
	cin>>u>>v;
	Root1 = Find(S, u - 1);
	Root2 = Find(S, v - 1);
	if (Root1 != Root2)
		Union(S, Root1, Root2);
}
//检查两个元素是否属于一个集合
void Check_connection(SetType S)
{
	ElementType u, v;
	SetName Root1, Root2;
	cin>>u>>v;
	Root1 = Find(S, u - 1);
	Root2 = Find(S, v - 1);
	if (Root1 == Root2)
		printf("yes\n");
	else printf("no\n");
}
//查看最后一共有几个集合
void Check_network(SetType S, int n)
{
	int i, counter = 0;
	for (i = 0; i<n; i++)
		if (S[i] < 0) counter++;
	if (counter == 1)
		printf("The network is connected.\n");
	else
		printf("There are %d components.\n", counter);
}

按秩归并

为什么要按秩归并
举例说明：一直将元素1所在集合合并到其他集合，整个树的结构就会失衡，树高度较大，Find()时间复杂度为O(n)，对n个结点操作，复杂度为O(n²)

解决方法1：把较矮的树合并到较高的树上去

将树的高度存放在根节的元素中
S[Root]= - 树高
S[Root]初始化时，仍然初始化为-1

if (S[Root2] < S[Root1])	//S[Root2]高度大，集合1合并到集合2
	S[Root1] = Root2;
else
{
	if (S[Root1] == S[Root2]) S[Root1]--;//集合高度相等，合并后高度增加
	S[Root2] = Root1;
}

最坏情况下，每次合并高度都相等，树高 = O(log N)

解决方法2：比规模，把小树贴到大树上

S[Root]= - 元素个数;

void Union(SetType S, SetName Root1, SetName Root2)
{
	if (S[Root2]<S[Root1])	//S[Root1]所在树规模较小
	{
		S[Root2] += S[Root1];//树的规模变为二者元素个数之和
		S[Root1] = Root2;
	}
	else 
	{
		S[Root1] += S[Root2];
		S[Root2] = Root1;
	}
}

两种方法统称“按秩归并”

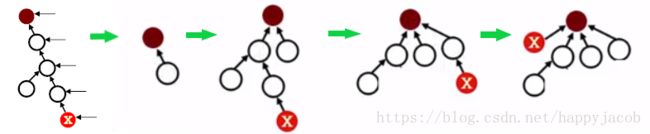
路径压缩

SetName Find(SetType S, ElementType X)
{
	if (S[X] < 0)		//找到集合的根
		return X;
	else
		return S[X] = Find(S, S[X]);
}

这段代码干了三件事

1. 先找到根；
2. 把根变成X 的父结点；
3. 再返回根。

路径压缩第一次执行的时间比较长，但是如果频繁使用查找命令，第一次将路径压缩，大大减小树的高度，后续查找速度将大大增加