剑指offer笔试题

1、多种排序算法比较

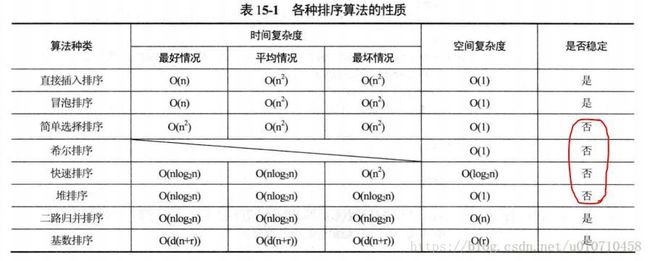
1、归并排序
分治思想：大问题分割成小问题解决，然后用所有小问题的答案来解决整个大问题。
归并排序是建立在归并操作上的一种有效的排序算法。该算法是分治法的一个非常典型的应用。首先考虑下如何将将二个有序数列合并。只要从比较二个数列的第一个数，谁小就先取谁，取了后就在对应数列中删除这个数。然后再进行比较，如果有数列为空，那直接将另一个数列的数据依次取出即可，也就是下面merge实现的代码。
要将一个数组排序，可以先（递归地）将它分成两半分别排序，然后将结果归并起来。归并排序最吸引人的性质就是可以保证任意长度为N的数组排序所需要时间和NlgN成正比，缺点在于需要额外和N成正比的辅助空间。

static int less(Item a ,Item b)//为了是程序通用化，修改比较程序即可。
{
    if(a < b)
        return 1;
    else
        return 0;
}
static void exch(Item *a , int i , int j)
{
    Item swap = a[i];
    a[i] = a[j];
    a[j] = swap;
}
bool isSort(Item *a , int N)
{
    for(int i =1 ; iif(less(a[i] , a[i-1]))
            return false;
    }
    return true;
}
void DispalyItems(const Item *a , int N)
{
    for(int i = 0 ; i < N ; i++)
        printf("%4d",a[i]);
    printf("\n");
}
void SelectionSort(Item *a , int N)//选择排序
{
    int i , j;
    int min;//记录最小项索引
    for(i = 0 ; i < N ; i++ ){
        min = i;
        for(j = i + 1 ; j< N ; j++)//找出后面最小项索引并记录
            if(less(a[j] , a[min]))
                min = j;
        exch(a , i , min);//最后一项自己和自己交换不变。
    }
}
void InsertionSort(Item *a , int N)//插入排序
{
    int i , j;
    for( i = 0 ; i < N ; i++)
        for(j = i ; j > 0 ; j--){
            if(less(a[j] , a[j-1]))//插入前面已经排好序项目中
                exch(a , j , j-1);
            else
                break;//可以停止了因为前面已经排好序了不必继续遍历
        }
}
void BubbleSort(Item *a , int N)//冒泡排序
{
    int i ,j;
    for(i = 0 ; i < N ; i++)
        for(j = i+1 ; jif(less(a[j] , a[i]))//插入前面已经排好序项目中
                exch(a , i , j);
}
void ShellSort(Item *a , int N)//希尔排序和插入排序很像
{
    int i , j;
    int h = 1;//间隔大小
    while(h < N/3) h = 3 * h +1;//计算最大间隔。运用高纳德的 3n+1序列
    for( ; h >= 1 ; h /= 3 ){//h间隔一层循环
        for( i = h ; i < N ; i++)
            for(j = i ; j >= h ; j -= h){
                if(less(a[j] , a[j-h]))//插入前面已经排好序项目中
                    exch(a , j , j-h);
                else
                    break;//可以停止了因为前面已经排好序了不必继续遍历
            }
    }
}


/**************自顶向下归并排序   归并排序****************/
static void merge(Item *a , Item *aux , int lo , int mid , int hi)
{
    for(int k = lo ; k <= hi ; k++)
        aux[k] = a[k];//将a数组复制到aux
    int i = lo , j = mid + 1;
    for(int k = lo ; k <= hi ; k++){//合并
        if( i  > mid) a[k] = aux[j++];//左边数据取完
        else if(j > hi) a[k] = aux[i++];//右边数据取完
        else if( less(aux[j] , aux[i]) ) a[k] = aux[j++];//
        else a[k] = aux[i++];
    }
}
static void MSort(Item *a , Item *aux , int lo , int hi)
{
    if(hi <= lo) return ;
    int mid = lo + (hi - lo)/2;
    MSort(a , aux , lo , mid);//左半边排序
    MSort(a , aux , mid+1 , hi);//右半边排序
    merge(a , aux , lo , mid , hi);//归并
}
void MergeSort(Item *a , int N)
{
    Item *aux = (Item *)malloc(N * sizeof(Item));
    MSort(a , aux , 0 , N - 1);//递归调用
    free(aux);//释放缓冲空间
}

/************自低向上归并排序***************/
#define MIN(a , b) ( (a) > (b) ) ? (b) : (a)
static void MSort(Item *a , Item *aux , int lo , int hi)
{
    if(hi <= lo) return ;
    int mid = lo + (hi - lo)/2;
    MSort(a , aux , lo , mid);//左半边排序
    MSort(a , aux , mid+1 , hi);//右半边排序
    merge(a , aux , lo , mid , hi);//归并
}
void MergeBUSort(Item *a , int N)
{
    int sz , lo;
    Item *aux = (Item *)malloc(N * sizeof(Item));
    for(sz = 1 ; sz < N ; sz = sz + sz ){//sz子数组大小
        for( lo = 0 ; lo < N - sz ; lo += sz + sz){//lo子数组索引
            merge(a , aux , lo , lo+sz-1 , MIN(lo+sz+sz-1 , N-1));
        }
    }
    free(aux);//释放缓冲空间
}

第一次只出现一次的字符

题目描述
在一个字符串(0<=字符串长度<=10000，全部由字母组成)中找到第一个只出现一次的字符,并返回它的位置, 如果没有则返回 -1（需要区分大小写）.

class Solution {
public:
    /*
    1、map记录字符和次数
    2、遍历字符串，依次判断位置和次数即可
    */
    int FirstNotRepeatingChar(string str) {

        int length = str.length(); 
        //map m; //可以定义map或者自定义hash数组，因为char仅仅只有256中情况
        unsigned int m[256] = {0};//这里实现的效果一样，因为是为了记录字符次数
        for(int i = 0 ; i < length ; i++)
            m[str[i]]++;//记录次数
        for(int i = 0 ; i < length ; i++)
            if(m[str[i]] == 1)
                return i;
        return -1;
    }
};

扩展：
1、定义一个函数，输入两个字符串。从第一个字符串中删除在第二个字符串中出现过的所有字符。例如”We are students.”删除”aeiou”中出现的字符，得到”W r Stdnts”。(OPPO面试题)
创建一个数组记录数组2中的字符，然后遍历1先判断，则决定是否保留。

char *remove(char *str1 , char *str2)
{
    if(str == NULL)
        return NULL;
    bool hashtable[256] = {false};
    int length1 = strlen(str1);
    int length2 = strlen(str2);
    char *res = (char *)malloc(length+1);//结束符留位置
    for(int i = 0 ; i < length2 ; i++)//标记
        hashtable[str2[i]] = true;
    int index = 0;
    for(int i = 0; i < length1 ; i++){
        if(!hashtable[str1[i]])//如果1中没有出现，则记录
            res[index++] = str1[i];
    }
    res[index] = '\0';
    return res;
}

2、删除字符串中所有重复出现的字符
google -> gole。
一个bool hash[256],每次扫描都先判断字符是否出现过，出现则删除，否则标记出现。复杂度是O(n).
3、如果两个单词中出现的字母相同，并且每个字符出现的次数相同，那么两个单词称为变位词。
一个hash[256]表，扫描第一个记录+1，扫描第二个-1，如果最后hash都为0，则是变位词。

单词翻转和左旋

/*
 * 翻转单词顺序
 * I am a student. -> student. a am I
 * 思路： 1、先整体翻转。
 *       2、然后根据空格分割再逐步翻转。
*/
#include
#include
#include
void reverse(char *temp, int i , int j)//前后指针翻转字符串
{
    if(!temp)//防御性编程
        return ;
    while(i < j){
        char a = temp[i];
        temp[i] = temp[j];
        temp[j] = a;
        i++;
        j--;
        if(i == j)//长度是奇数，就会碰到相等直接退出即可。
            break;
    }
}
//翻转句子
void reverseSentence(char *str)
{
    if(str == NULL)
        return ;
    int strLength = strlen(str);//字符串长度
    int start = 0;
    int end = strLength - 1;
    //1、整体翻转
    reverse(str , start , end);

    //2、依据空格逐个翻转单词，通过一个i遍历，然后start和end记录每个单词的初始化位置
    start = 0;
    end = 0;
    int i = 0 ;
    while(i < strLength){
        while (i < strLength && str[i] ==' ')//跳过单词前面的空格，并记录单词首个字母索引
            i++;
        start = end = i;
        while (i < strLength && str[i] != ' ') {//找到单词末尾
            i++;
            end++;
        }
        reverse(str , start , end - 1);//翻转单词，然后接着通过i继续遍历即可
    }
}
//扩展 字符串左旋操作。要求abcdefg变成cdefgab 和前面完全一样，简单翻转三次即可
//abcdefg -> bagfedc(翻转两部分) -> cdefgab(在整体翻转)
void leftRotateString(char *str , int k)
{
    if(str == NULL || k == 0)//防御性编程
        return ;
    int strLength = strlen(str);
    if(k >= strLength)
        return;
    int firstStart = 0;
    int firstEnd = k - 1;
    int secondStart = k;
    int secondEnd = strLength - 1;
    reverse(str , firstStart , firstEnd);
    reverse(str , secondStart , secondEnd);
    reverse(str , 0 , strLength-1);
}
int main(void)
{
    char str[] = " I am a student. ";
    char str1[] = "abcdefg";
    reverseSentence(str);
    printf("%s\n" , str);
    leftRotateString(str1 , 6);
    printf("%s\n" , str1);
}

atoi

将一个字符串转换成一个整数，要求不能使用字符串转换整数的库函数。 数值为0或者字符串不是一个合法的数值则返回0。 一定要注意边界条件，你知道不？？？明白就好。

class Solution {
public:
   /*
   策略则是遍历一遍字符串即可。
    1、地址有效NULL或空字符串
    2、数据是否上下溢出
    3、有无正负号
    4、错误标志输出
   */
    enum Status{kValid = 0 , kInvalid};
    int g_nStatus = kValid;//全局标志 
    int StrToInt(string str) {
        g_nStatus = kInvalid;
        long long num = 0;//long long 8字节，但是int 4字节，所以千万不能越界，占用4字节 最大为7f-ff-ff-ff 最小为 80-00-00-00
        const char* cstr = str.c_str();//将str转换成c字符串形式，也就是指针指向内存区域。
        if( (cstr != NULL) && (*cstr != '\0') )//1、防御性编程 字符存在且第一个非空，则继续处理
        {
            int minus = 1;//标记字符串符号
            if(*cstr == '-')//第一个为减号
            {
                minus = -1;
                cstr++;//指向下一个字符
            }
            else if(*cstr == '+')//第一个为加号
                cstr++;

            while(*cstr != '\0')//循环处理全部字符
            {
                if(*cstr > '0' && *cstr < '9')//为数字
                {
                    g_nStatus = kValid;//因为是数字，则有效。
                    //2345 =  ( ( (0*10+2) * 10 + 3)*10+4 )*10 + 5 这就是霍顿算法。
                    //这种迭代很聪明
                    num = num * 10 + (*cstr -'0');//字符串转换数字迭代计算
                    cstr++;//指向下一个
                    if( ( (minus > 0) && (num > 0x7FFFFFFF) ) ||
                        ( (minus < 0) && (num < (int)0x80000000) ) )//是否越界？
                    {
                        g_nStatus = kInvalid;//无效，返回0
                        return 0;//无效，则直接返回0
                    }
                }
                else
                {
                    g_nStatus = kInvalid;//中间含有非数字字符串，则标记此无效
                    return 0;
                }
            }
            return (num*minus);
        }
        g_nStatus = kInvalid;//无效，则直接返回0,并且标记无效。
        return 0;
    }
};

2、二叉树的四种遍历递归与递归实现

1、前序：
非递归实现：
根据前序遍历访问的顺序，优先访问根结点，然后再分别访问左孩子和右孩子。即对于任一结点，其可看做是根结点，因此可以直接访问，访问完之后，若其左孩子不为空，按相同规则访问它的左子树；当访问其左子树时，再访问它的右子树。因此其处理过程如下，对于任一结点P：
1)访问结点P，并将结点P入栈;
2)判断结点P的左孩子是否为空，若为空，则取栈顶结点并进行出栈操作，并将栈顶结点的右孩子置为当前的结点P，循环至1);若不为空，则将P的左孩子置为当前的结点P;
3)直到P为NULL并且栈为空，则遍历结束。

2、中序：
根据中序遍历的顺序，对于任一结点，优先访问其左孩子，而左孩子结点又可以看做一根结点，然后继续访问其左孩子结点，直到遇到左孩子结点为空的结点才进行访问，然后按相同的规则访问其右子树。因此其处理过程如下，对于任一结点P，
　1)若其左孩子不为空，则将P入栈并将P的左孩子置为当前的P，然后对当前结点P再进行相同的处理；
　 2)若其左孩子为空，则取栈顶元素并进行出栈操作，访问该栈顶结点，然后将当前的P置为栈顶结点的右孩子；
　3)直到P为NULL并且栈为空则遍历结束。
　
3、后序：
后序遍历的非递归实现是三种遍历方式中最难的一种。因为在后序遍历中，要保证左孩子和右孩子都已被访问并且左孩子在右孩子前访问才能访问根结点，这就为流程的控制带来了难题。下面介绍两种思路。
第一种思路：对于任一结点P，将其入栈，然后沿其左子树一直往下搜索，直到搜索到没有左孩子的结点，此时该结点出现在栈顶，但是此时不能将其出栈并访问， 因为其右孩子还未被访问。所以接下来按照相同的规则对其右子树进行相同的处理，当访问完其右孩子时，该结点又出现在栈顶，此时可以将其出栈并访问。这样就保证了正确的访问顺序。可以看出，在这个过程中，每个结点都两次出现在栈顶，只有在第二次出现在栈顶时，才能访问它。因此需要多设置一个变量标识该结点是否是第一次出现在栈顶。

//二叉树前序遍历 根 左 右
void PreoderRecursion(TreeNode *pRoot)
{
    if(pRoot == NULL)//返回
        return ;
    cout << pRoot->val;
    Preoder(pRoot->left);
    Preoder(pRoot->right);
}
void Preoder(TreeNode *pRoot)
{
    stack<TreeNode *>s;
    while(pRoot != NULL || !s.empty()){
        while(pRoot != NULL){//将左子树全部压栈
            s.push(pRoot);
            cout << pRoot->val;
            pRoot = pRoot->left;
        }
        if(!s.empty()){
            pRoot = s.top();
            s.pop();
            pRoot = pRoot->right;
        }
    }
}
//二叉树中序遍历  左 根 右
void inOderRecursion(TreeNode *pRoot)
{
    if(pRoot == NULL)//返回
        return ;
    Preoder(pRoot->left);
    cout << pRoot->val;
    Preoder(pRoot->right);
}
void Preoder(TreeNode *pRoot)
{
    stack<TreeNode *>s;
    while(pRoot != NULL || !s.empty()){
        while(pRoot != NULL){//将左子树全部压栈
            s.push(pRoot);
            pRoot = pRoot->left;
        }
        if(!s.empty()){
            pRoot = s.top();
            cout << pRoot->val;
            s.pop();
            pRoot = pRoot->right;
        }
    }
}
//二叉树后序遍历 左 右 根   通过一个栈实现，1、左右都遍历完了再遍历根。2、左右已经遍历完了 否则先压右子树再左子树
void PostOderRecursion(TreeNode *pRoot)
{
    if(pRoot == NULL)//返回
        return ;
    Preoder(pRoot->left);
    Preoder(pRoot->right);
    cout << pRoot->val;
}
void PostOder(TreeNode *pRoot)
{
    stack<TreeNode *>s;
    TreeNode *hasVisit = NULL;
    if(pRoot != NULL){
        s.push(pRoot);
        while (!s.empty()) {
            pRoot = s.top();
            if( (pRoot->left == NULL && pRoot->right == NULL) ||
                    ((pRoot->left != NULL || pRoot->right != NULL) && hasVisit != NULL)){//没有左右孩子，或者有且访问过了，则可以访问此节点
                cout <<pRoot->val;
                hasVisit = pRoot;//标记此节点已经访问了
                s.pop();
            }else{//否则压入 右子树和左子树
                if(pRoot->right != NULL)
                    s.push(pRoot->right);
                if(pRoot->left != NULL)
                    s.push(pRoot->left);
            }
        }
    }
}
//二叉树广度（层序）通过一个队列实现
//入队，弹出，访问，左右子树入队，循环上述过程
void BFSOder(TreeNode *pRoot)
{
    queue<TreeNode *> q;
    if(pRoot == NULL)//防御性编程
        return ;
    q.push(pRoot);
    while (!q.empty()) {
        pRoot = q.front();
        q.pop();
        cout << pRoot->val;

        if(pRoot->left != NULL)//入队
            q.push(pRoot->left);

        if(pRoot->right != NULL)//入队
            q.push(pRoot->right);
    }
}

3、二维数组查找

题目描述
在一个二维数组中（每个一维数组的长度相同），每一行都按照从左到右递增的顺序排序，每一列都按照从上到下递增的顺序排序。请完成一个函数，输入这样的一个二维数组和一个整数，判断数组中是否含有该整数。

class Solution {
public:
    /*
    因为递增规律，所以可以从左上角开始比较，目标数比其大，则下移，比其小则左移
    直到while循环结束。
    */
    bool Find(int target, vector<vector<int> > array) {
        if(array.size() == 0)//防御性编程
            return false;
        int i = 0 , j = array[0].size() - 1;
        while(i < array.size() && j >= 0){//i代表行，j代表列
            if(array[i][j] == target)
                return true;
            else if(array[i][j] < target)
                i++;
            else
                j--;
        }
        return false;
    }
};

4、替换空格

题目描述
请实现一个函数，将一个字符串中的每个空格替换成“%20”。例如，当字符串为We Are Happy.则经过替换之后的字符串为We%20Are%20Happy。

class Solution {
public:
    /*
    第一种方法：新分配内存存储
    动态分配内存，将字符串移动到新的一块内存上，并返回。
    char * replaceSpace(const char *str) {
    int NumOfSpace = 0;
    int StrLength = 0;
    const char *temstr = str;
    if(temstr == NULL)//防御性编程，空则直接返回
        return NULL;

    while(*temstr != '\0'){//统计字符串长度及空格数量
        if(*temstr == ' ')
            NumOfSpace++;
        StrLength++;
        temstr++;
    }
    int newStrLength = StrLength + NumOfSpace*2;//新字符串长度

    char *newStr = (char *)malloc(newStrLength + 1);//+1是为了给结束符留内存。

    int i = StrLength , j = newStrLength;

    while(i >= 0){//直到1中重复复制完成
        if(str[i] == ' '){//如果是空格,则复制
            i--;
            newStr[j--] = '0';
            newStr[j--] = '2';
            newStr[j--] = '%';
        }
        newStr[j--] = str[i--];
    }

    return newStr;
}
    */


    /*
    第二种方法：在原内存上面移动
    1、遍历一遍，获取空格个数，并扩容，length代表可用长度，如果小则返回，否则扩容处理
    2、设置两个指针i ， j 分别指向新旧字符串，将旧字符串，从后往前复制到新内存，可以最少避免重复移动字符串
    */
    void replaceSpace(char *str,int length) {
        int NumOfSpace = 0;
        int StrLength = 0;
        char *tempstr = str;
        if(str == NULL )//防御性编程，空则直接返回
            return ;
        while(*tempstr != '\0'){//统计字符串长度及空格数量
            if(*tempstr == ' ')
                NumOfSpace++;
            StrLength++;
            tempstr++;
        }
        int newStrLength = StrLength + NumOfSpace*2;//新字符串长度,注意此长度不包括空格

        if(newStrLength + 1 > length)//防御性编程，确保题目给的内存空间充足
            return ;

        int i = StrLength , j = newStrLength;
        while(i != j){//当i=j则表示空格已经替换完毕
            if(str[i] == ' '){//如果是空格,则复制
                i--;
                str[j--] = '0';
                str[j--] = '2';
                str[j--] = '%';
            }else
                str[j--] = str[i--];
        }
    }
};

5、从尾到头打印链表

题目描述
输入一个链表，按链表值从尾到头的顺序返回一个ArrayList

/**
*  struct ListNode {
*        int val;
*        struct ListNode *next;
*        ListNode(int x) :
*              val(x), next(NULL) {
*        }
*  };
*/
class Solution {
public:
    /*
    1、递归模拟栈

    void printList(vector &a , ListNode* head){
       if(head == NULL)//防御性编程
           return ;
        printList(a , head->next);
        a.push_back(head->val);
    }
    vector printListFromTailToHead(ListNode* head) {
        vector res;
        stack s;//辅助栈
        if(head == NULL)//防御性编程
            return res;
        printList(res , head);
        return res;
    }*/

    /*
    2、使用栈
    */
    vector<int> printListFromTailToHead(ListNode* head) {
            vector<int> res;
        stack<int> s;//辅助栈
        if(head == NULL)//防御性编程
            return res;
        while(head != NULL){//全部压栈
            s.push(head->val);
            head = head->next;
        }
        while(!s.empty()){//全部出栈，压入vector
            res.push_back(s.top());
            s.pop();
        }
        return res;
    }
};

6、求单链表中的倒数第k个节点

输入一个键表，输出该链表中倒数第k个结点。为了符合人们的习惯，本题从1开始计数，即链表的尾结点是倒数第1个结点。一个链表有6个结点，从头结点开始它们的值依次是 1 、 2、 3、 4、 5、 6。这个链表的倒数第3个结点是值为4的结点。
思路：删除倒数第k个节点，就是相当于删除从头到尾第n-k+1个节点。
方法一：遍历两次，第一次获取链表长度，第二次删除节点。
方法二：定义两个指针。第一个指针从链表的头指针开始遍历向前走k-1步，第二个指针保持不动；从第k步开始，第二个指针也开始从链表的头指针开始遍历。由于两个指针的距离保持在k-1，当第一个（走在前面的）指针到达链表的尾结点时，第二个指针（走在后面的）正好是倒数第k个结点。下图可以看出打印倒数第k个节点，那么到了最后p1比p2多走了k-1步。这样就很容易了。

struct ListNode *FindKthToTail(struct ListNode *pListHead , unsigned char k)
{
    //防御性编程,头节点为空,k为0
    if(pListHead == NULL || k == 0)
        return NULL;
    struct ListNode *p1 = pListHead;
    struct ListNode *p2 = pListHead;
    //1、先走k-1步咯
    for(int i = 0 ; i < k - 1 ; i++){
        if(p1->pNext != NULL)//防止k比节点个数多的情况
            p1 = p1->pNext;
        else
            return NULL;
    }
    //2、再一起走到底咯
    while(p1->pNext != NULL){
        p1 = p1->pNext;
        p2 = p2->pNext;
    }
    return p2;
}

7、单链表反转

题目：定义一个函数，输入一个链表的头结点，反转该链表并输出反转后链表的头结点。
思路：记住前一个结点和后一个节点的信息，然后遍历一次链表，遍历开始时候确定前一个节点和后一个节点信息都为空，在循环里面更新信息。
注意：
1、输入pListHead == NULL。
2、输入链表只有一个节点。
3、输入链表有多个节点。

struct ListNode *ReverseList(struct ListNode *pListHead)
{
    //防御性编程,防止链表为空
    if(pListHead == NULL)
        return pListHead;
    //1.正常反转,记住当前节点的前一个节点和后一个节点,这里已经防御了只有一个节点的情况
    struct ListNode *CurrentNode = pListHead;//当前节点
    struct ListNode *PreNode = NULL;//前一个节点,初始化前一个节点为空
    struct ListNode *NextNode = NULL;//后一个节点
    while(CurrentNode != NULL){
        NextNode = CurrentNode->pNext;//更新后一个节点信息
        CurrentNode->pNext = PreNode;//反转当前节点,指向前一个节点
        if(NextNode == NULL)
            return CurrentNode;//如果到达链表尾,则直接返回.
        PreNode = CurrentNode;//更新前一个节点
        CurrentNode = NextNode;//更新当前一个节点
    }
}

8、合并两个已排序的单链表（必考）

题目：输入两个递增排序的链表，合并这两个链表并使新链表中结点仍然是按照递增排序的。

struct ListNode *MergeListRecursive(struct ListNode *pListHead1 , struct ListNode *pListHead2)
{
    struct ListNode *pMergeHead;//指向合并链表头部
    //防御性编程.
    if(pListHead1 == NULL)
        return pListHead2;
    else if(pListHead2 == NULL)
        return pListHead1;
    //1.比较键值,并递归下去
    if(pListHead1->key < pListHead2->key){
        pMergeHead = pListHead1;
        pMergeHead->pNext = MergeListRecursive(pListHead1->pNext , pListHead2);
    }else{
        pMergeHead = pListHead2;
        pMergeHead->pNext = MergeListRecursive(pListHead1 , pListHead2->pNext);
    }
    return pMergeHead;//返回对应的键
}

9、单链表排序

快速排序重要的是切分思路：
快排需要一个指针指向头，一个指针指向尾，然后两个指针相向运动并按一定规律交换值，最后找到一个支点使得支点左边小于支点，支点右边大于支点吗。如果是这样的话，对于单链表我们没有前驱指针，怎么能使得后面的那个指针往前移动呢？所以这种快排思路行不通滴，如果我们能使两个指针都往next方向移动并且能找到支点那就好了。怎么做呢？
接下来我们使用快排的另一种思路来解答。我们只需要两个指针p和q，这两个指针均往next方向移动，移动的过程中保持p之前的key都小于选定的key，p和q之间的key都大于选定的key，那么当q走到末尾的时候便完成了一次支点的寻找。如下图所示：

//单链表快速排序
void swap(int *a , int *b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}
//切分思路区别于数组的切分思路
struct ListNode *Partition(struct ListNode *pBegin , struct ListNode *pEnd)
{
    struct ListNode *p = pBegin;
    struct ListNode *q = pBegin->pNext;
    while(q != pEnd){
        if(q->key < pBegin->key){
            p = p->pNext;
            swap( &p->key , &q->key );
        }
        q = q->pNext;
    }
    swap( &p->key , &pBegin->key );
    return p;//返回切分位置
}
//快速排序 O(logn)
void QuickSort(struct ListNode *pBegin , struct ListNode *pEnd)
{
    if(pBegin == pEnd)
        return ;
    struct ListNode *j = Partition(pBegin , pEnd);
    QuickSort(pBegin , j);
    QuickSort(j->pNext , pEnd);
}
//冒泡排序 O(n*n)
void ListBubble(struct ListNode *pBegin)
{
    if(pBegin == NULL || pBegin->pNext == NULL)
        return ;
    struct ListNode *i = pBegin;
    struct ListNode *j;
    for( ; i != NULL ; i = i->pNext)
        for(j = i->pNext ; j != NULL ; j = j->pNext){
            if(i->key > j->key)
                swap( &i->key , &j->key );
        }
}

10、寻找单链表的中间节点

思路：
1、正常方法是，遍历一次链表，找出链表长度，然后取出中间节点。这种方法需要遍历两次，效果不好。
2、使用快慢指针，开始快和慢指针全部指向首节点；然后快指针每次走两步，慢指针每次走一步，当pFast == NULL//对应节点偶数个或pFast->pNext == NULL//对应节点为奇数个，则遍历结束，返回慢节点。画个简单的图形就可以明白这个过程。
注意：
1、防御性编程，注意鲁棒性。
2、尽可能遍历一遍链表就可以解决问题，这是我们喜欢的方式。

struct ListNode *SearchMid(struct ListNode *pListHead)
{
    struct ListNode *pSlow = pListHead;
    struct ListNode *pFast = pListHead;
    //防御性编程
    if(pListHead == NULL)
        return NULL;
    //开始快慢遍历,pFast为空对应节点为奇数，则返回中间节点。pFast->pNext为空,对应节点为偶数，则返回中间两个节点的后一个。
    while(pFast != NULL && pFast->pNext != NULL){
        pFast = pFast->pNext->pNext;//走两步
        pSlow = pSlow->pNext;//走一步
    }
    return pSlow;//返回中间节点
}

11、求有环单链表中的环长、环起点、链表长

1、判断单链表是否有环：
　　使用两个slow, fast指针从头开始扫描链表。指针slow 每次走1步，指针fast每次走2步。如果存在环，则指针slow、fast会相遇；如果不存在环，指针fast遇到NULL退出。

//判断链表是否有环
struct ListNode *JudgeRing(struct ListNode *pListHead)
{
    struct ListNode *pSlow = pListHead;
    struct ListNode *pFast = pListHead;
    //防御性编程
    if(pListHead == NULL)
        return NULL;
    while(1){
        //如果pFast先退出,那么就是没有环,如果fast退不出,那么就是有环
        if(pSlow->pNext != NULL && pFast->pNext != NULL && pFast->pNext->pNext != NULL){
            pFast = pFast->pNext->pNext;//走两步
            pSlow = pSlow->pNext;//走一步
        }else
            return NULL;
        if(pFast == pSlow)
            return pFast;
    }
}

2、求有环单链表的环长：
　　在环上相遇后，记录第一次相遇点为Pos，之后指针slow继续每次走1步，fast每次走2步。在下次相遇的时候fast比slow正好又多走了一圈，也就是多走的距离等于环长，相当于在圆形操场同一起点两人跑步，下一次相遇，不是正好快的比慢的多跑一圈。
　　设从第一次相遇到第二次相遇，设slow走了len步，则fast走了2*len步，相遇时多走了一圈：
　　　　环长=2*len-len。
　　就是所谓的追击相遇问题。

int GetRingLength(struct ListNode *pListHead)
{
    //防御性编程
    if(pListHead == NULL)
        return 0;
    struct ListNode *ringMeetNode = JudgeRing(pListHead);//判断是否有环,并记录相遇点

    if(ringMeetNode == NULL)
        return 0;//无环直接退出
    //有环,从相遇点在fast和slow走一遍就是再次相遇就是环长.
    int RingLength = 0;
    struct ListNode *pSlow = ringMeetNode;
    struct ListNode *pFast = ringMeetNode;
    while(1){
        pFast = pFast->pNext->pNext;
        pSlow = pSlow->pNext;
        RingLength++;
        if(pFast == pSlow)//相遇了,返回环长
            return RingLength;
    }
}

3、求有环单链表的环连接点位置：
　　第一次碰撞点Pos到连接点Join的距离 = 头指针到连接点Join的距离，因此，分别从第一次碰撞点Pos、头指针head开始走，相遇的那个点就是连接点。
在环上相遇后，记录第一次相遇点为Pos，连接点为Join，假设头结点到连接点的长度为LenA，连接点到第一次相遇点的长度为x，环长为R。
　　　　第一次相遇时，slow走的长度 S = LenA + x;
　　　　第一次相遇时，fast走的长度 2S = LenA + n*R + x;
　　　　所以可以知道，LenA + x = n*R;　　LenA = n*R -x;此处令n=1，即可。

struct ListNode *GetRingJoinNode(struct ListNode *pListHead , int *length)
{
    //防御性编程
    if(pListHead == NULL)
        return 0;
    struct ListNode *ringMeetNode = JudgeRing(pListHead);//判断是否有环,并记录相遇点
    if(ringMeetNode == NULL)
        return 0;//无环直接退出
    //求相交点,head和相遇点一起走,再次相遇则是相交点
    while (1) {
        ringMeetNode = ringMeetNode->pNext;
        pListHead = pListHead->pNext;
        (*length)++;//头节点到交点的长度
        if(ringMeetNode == pListHead)
            return ringMeetNode;
    }
}

4、求有环单链表的链表长
上述2中求出了环的长度；3中求出了连接点的位置，就可以求出头结点到连接点的长度。两者相加就是链表的长度。

12、判断两个单链表(无环)是否交叉并求交点

判断是否相交突破口：如果两个没有换的链表相交于一点，那么在这个节点之后的所有节点都是两个链表共同拥有的，那么也就是最后一个节点一定是共有的。
解法：很简单，先遍历一个链表，记住最后一个节点。然后遍历第二个，到最后一个节点时候和先前记住的节点比较。时间复杂度是O(length(list1) + length(list2))。而且仅仅用了一个变量，空间复杂度是O(1)。
求交点突破口：判断出两个链表相交后就是判断他们的交点了。假设第一个链表长度为len1，第二个为len2，然后找出长度较长的，让长度较长的链表指针向后移动|len1 - len2| (len1-len2的绝对值)，然后在开始遍历两个链表，判断节点是否相同即可。

//判断单链表是否相交,并求出节点
struct ListNode *JudgeCrossListAnd(struct ListNode *pListHead1 , struct ListNode *pListHead2)
{
    //防御性编程
    struct ListNode *pTemp1 = pListHead1;
    struct ListNode *pTemp2 = pListHead2;
    if(pTemp1 == NULL || pTemp2 == NULL)
        return NULL;
    int List1Length = 0 , List2Length = 0;
    while(pTemp1->pNext != NULL){//找到List1尾部节点
        pTemp1 = pTemp1->pNext;
        List1Length++;
    }
    List1Length++;//求1长度
    while(pTemp2->pNext != NULL){//找到List1尾部节点
        pTemp2 = pTemp2->pNext;
        List2Length++;
    }
    List2Length++;//求2长度
    if(pTemp1 == pTemp2){//相交则求交点
        if(List1Length > List2Length){//链表1比链表2长,链表1先走
            for(int i = 0 ; i < (List1Length - List2Length) ; i++)
                   pListHead1 = pListHead1->pNext;
            while(pListHead1 != pListHead2){
                pListHead1 = pListHead1->pNext;
                pListHead2 = pListHead2->pNext;
            }
            return pListHead2;//找到交点
        }else{//链表1比链表2短,链表2先走
            for(int i = 0 ; i < (List2Length - List1Length) ; i++)
                   pListHead2 = pListHead2->pNext;
            while(pListHead1 != pListHead2){
                pListHead1 = pListHead1->pNext;
                pListHead2 = pListHead2->pNext;
            }
            return pListHead2;//找到交点
        }
    }
    else
        return NULL;
}

13、删除单链表中重复的结点（必考）

在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点，重复的结点不保留，返回链表头指针。 例如，
1、链表1->2->3->3->4->4->5 处理后为 1->2->5
2、 链表1->2->3->3->4->4->5 处理后为 1->2->3->4->5的区别
通过画图就可以区分如何做了？
首先建立空节点，然后通过两个指针进行比较即可。

class Solution {
public:
    /*
    1、链表有序，所以可以遍历实现。然后就是仔细画图了，相当重要的。
    */
    ListNode* deleteDuplication(ListNode* pHead)
    {
        if(pHead == NULL || pHead->next == NULL)//没有节点或者只有一个节点，则直接返回。
            return pHead;
        ListNode Head(0);//存储头节点，防止先前头结点重复了
        Head.next = pHead;
        ListNode *preNode = &Head;//最近没有重复的节点
        ListNode *curNode = pHead;//探寻重复的节点，前进
        while(curNode != NULL){
            if(curNode->next != NULL && curNode->val == curNode->next->val){//相等，curNode继续往后面寻找
                while(curNode->next != NULL && curNode->val == curNode->next->val)//一直寻找,直到某个值不等
                    curNode = curNode->next;
                preNode->next = curNode->next;//不保留重复点指向下一个节点，针对题目1
                //preNode->next = curNode;//保留一个重复点，指向下一个节点，针对题目2
                curNode = curNode->next;//指向下一个不等的节点
            }else{//不相等，则一起前进一步
                preNode = preNode->next;//指向当前没有重复的节点
                curNode = curNode->next;//指向下一个
            }
        }
        return Head.next;
    }
};

14、以O(1)复杂度删除链表中给定的节点

方法一：删除结点i之前 ， 先从链表的头给点开始边历到i前面的一个结点h，把h的pNext指向i的下一个结点再删除结点i。请注意特殊情况，详情见代码。
方法二：把给点 j 的内容复制覆盖结点i，接下来再把结点i的m_pNext指向j的下一个结点之后，删除结点j。这种方法不用遍历链表上结点i前面的结点。请注意特殊情况，详情见代码。
以上的前提是节点在链表中，否则必须遍历确认，那么就没有实质性了。并且首先应该考虑的就是防御性编程，在接口开始验证传入参数的正确性。

/*
遍历删除,时间复杂度是O(n)
注意:删除头节点和删除后面节点不一样.
*/
struct ListNode *DeleteNode_On(struct ListNode *pListHead , struct ListNode *pToBeDeleted)
{
    //边界判断,防御性编程
    if(pListHead == NULL || pToBeDeleted == NULL)
        return pListHead;
    //1、如果删除头节点,则直接返回头节点
    if(pListHead == pToBeDeleted){
        pListHead = pToBeDeleted->pNext;//保存下个节点信息
        free(pToBeDeleted);//删除本节点
        return pListHead;//返回头节点
    }
    //2、如果删除不是头节点,则遍历即可
    struct ListNode *pNode = pListHead;
    while(pNode->pNext != pToBeDeleted)//删除后面节点,则找到要删除的节点的前一个节点
        pNode = pNode->pNext;
    pNode->pNext = pToBeDeleted->pNext;//前一个节点链接起来,并删除
    free(pToBeDeleted);
    return pListHead;
}
/*
找到删除节点下一个节点,时间复杂度是O(1)
*/
struct ListNode *DeleteNode_O1(struct ListNode *pListHead , struct ListNode *pToBeDeleted)
{
    struct ListNode *pNode = pListHead;

    //边界判断,防御性编程
    if(pListHead == NULL || pToBeDeleted == NULL)
        return pListHead;

    //1.如果删除头节点,则直接返回头节点
    if(pListHead == pToBeDeleted){
        pListHead = pToBeDeleted->pNext;//保存下个节点信息
        free(pToBeDeleted);//删除本节点
        return pListHead;//返回头节点
    }
    //2.如果删除的是尾部节点,则利用遍历删除
    if(pToBeDeleted->pNext == NULL){
        while(pNode->pNext != pToBeDeleted)//找到删除山一个节点
            pNode = pNode->pNext;
        pNode->pNext = pToBeDeleted->pNext;//前一个节点链接起来,并删除
        free(pToBeDeleted);
        return pListHead;
    }

    //3.如果删除节点是中间节点,那么利用O(1)算法
    pNode = pToBeDeleted->pNext;//删除节点下一个节点
         //下个节点拷贝给删除节点
    pToBeDeleted->key = pNode->key;
    pToBeDeleted->pNext = pNode->pNext;
    free(pNode);//删除下一个节点
    return pListHead;
}

15、重建二叉树

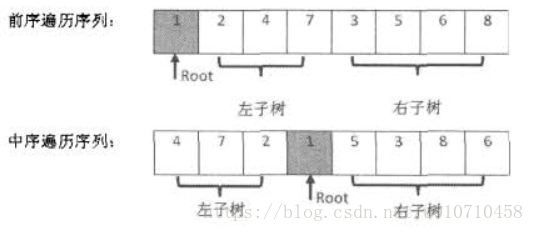
输入某二叉树的前序遍历和中序遍历的结果，请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6}，则重建二叉树并返回。

class Solution {
public:
    /*
    1、前序遍历第一个节点是根节点，中序遍历中间节点是根节点并将分为左右子树。
    2、然后递归进行构造左右子树。注意下述vector的使用方法。
    */
    TreeNode* reConstructBinaryTree(vector<int> pre,vector<int> vin) {
        if(pre.size()== 0 || vin.size() == 0)//防御性编程，且递归结束返回。
            return NULL;
        TreeNode* rootNode = new TreeNode(pre[0]);//新键根节点,且第一个节点值肯定是vin[0]
        vector<int>::iterator preIter = pre.begin();
        vector<int>::iterator vinIter = vin.begin();
        for(int i = 0 ; i < vin.size() ; i++){
            if(pre[0] == vin[i]){//找到中序的分叉点
                rootNode->left = reConstructBinaryTree( vector<int>(preIter+1 , preIter+i+1) , vector<int>(vinIter , vinIter+i) );//先构建左子树
                rootNode->right = reConstructBinaryTree( vector<int>(preIter+i+1 , pre.end()) , vector<int>(vinIter+i+1 , vin.end()) );//再构建右子树
            }
        }
        return rootNode;
    }
};

用两个栈实现队列

用两个栈来实现一个队列，完成队列的Push和Pop操作。 队列中的元素为int类型。

class Solution
{
public:
    /*
    利用栈先进后出的观点，将栈中元素弹出再次入栈，那么就是先进先出了
    1、入队：将元素进栈A。
    2、出队：判断栈B是否为空，如果为空，则将栈A中所有元素pop，并push进栈B（那么就是先进先出的排序了），栈B出栈；
       如果不为空（先前还有元素），因此可直接栈B直接出栈。
    */
    void push(int node) {//入队
        stack1.push(node);
    }
    int pop() {//出队
        if(stack2.empty()){
            while(!stack1.empty()){//循环取出栈1元素，并压入栈2
                stack2.push(stack1.top());
                stack1.pop();
            }
        }
        int temp = stack2.top();
        stack2.pop();
        return temp;
    }

private:
    stack<int> stack1;
    stack<int> stack2;
};

旋转数组最小值

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

特例： 没有旋转、1 0 1 1 1 、1 1 1 0 1等

class Solution {
public:
    /*
    因为是非递减排序，不是严格的递增排序，所以需要判断1,2,3及特例情况
    二分查找缩小范围的特例：
        1、如果中间元素>=头元素,那么此元素一定属于前面有序数组，则修改为mid
        2、如果中间元素<=尾元素,那么此元素一定属于后面有序数组，则修改为mid
        3、如果两个指针相差为1，则找到中间节点。
        特例：如果中间元素，头部元素，尾部元素一样，则不能通过二叉树，只能顺序遍历。
    */
int minNumberInRotateArray(vector<int> rotateArray) {
    if(rotateArray.size() == 0)//防御性编程
        return 0;
    int headIndex = 0;
    int tailIndex = rotateArray.size() - 1;
    int midIndex = (tailIndex + headIndex)/2;//二分或者是headIndex +  (tailIndex - headIndex)/2,一定需要注意这种写法

    //1、没有旋转,必须小于 则直接返回第一个元素即可
    if(rotateArray[headIndex] < rotateArray[tailIndex])
        return rotateArray[0];

    //2、判断特例只能循序查找   1 2 2 2 2 -》 2 1 2 2 2 或 2 2 2 1 2
    if(rotateArray[headIndex] == rotateArray[tailIndex] && rotateArray[midIndex] == rotateArray[tailIndex]){
        int min = rotateArray[0];
        for(vector<int>::iterator i = rotateArray.begin() ; i != rotateArray.end() ; i++){
            if(*i < min)
                min = *i;
        }
        return min;
    }

    //3、可进行二分查找了,通过两个排序数组，进一步缩小范围
    while(tailIndex > headIndex){
        if(tailIndex - headIndex == 1){
            return rotateArray[tailIndex];
        }else if(rotateArray[midIndex] >= rotateArray[headIndex])
            headIndex = midIndex;
        else if(rotateArray[midIndex] <= rotateArray[tailIndex])
            tailIndex = midIndex;
        midIndex = (tailIndex + headIndex)/2;//更新midIndex
    }
    return 0;
}
};

斐波那契数列

大家都知道斐波那契数列，现在要求输入一个整数n，请你输出斐波那契数列的第n项。
n<=39
记住禁止使用递归，容易导致栈溢出。

class Solution {
public:
    /*
    1、迭代方法,通过两个变量，记录前两个数即可。

    int Fibonacci(int n) {
        if(n < 0)
            return 0;
        if(n  == 1)
            return 1;
        if(n == 2)
            return 1;
        int firstNum = 1;
        int secondNum = 1;
        int result = 0;
        for(int i = 3 ; i <= n ; i++){
            result = firstNum + secondNum;
            firstNum = secondNum;
            secondNum = result;
        }
        return result;
        */
    /*
    */

    /*
    2、递归，可能产生栈溢出，慎用。并且F(3) F(4) 都被计算了两次，及其不可取。
        Fibonacci(4) = Fibonacci(3) + Fibonacci(2);
                     = Fibonacci(2) + Fibonacci(1) + Fibonacci(1) + Fibonacci(0);
                     = Fibonacci(1) + Fibonacci(0) + Fibonacci(1) + Fibonacci(1) + Fibonacci(0);
                     Fibonacci(0)和Fibonacci(1)重复计算了很多次。且存在函数的栈溢出。
    int Fibonacci(int n) {    
        if(n < 0)
            return 0;
        if(n  == 1)
            return 1;
        if(n == 2)
            return 1;
        return Fibonacci(n-1)+Fibonacci(n-2);
    }
    */
    /*
    3、动态规划
    */
    int Fibonacci(int n) {
        vector res;
        res.resize(n+1);//为了方便计算
                if(n < 0)
            return 0;
        if(n  == 1 || n == 2)
            return 1;
        res[1] = 1;
        res[2] = 1;
        for(int i =3 ; i <= n ; i++)
            res[i] = res[i-1] + res[i-2];
        return res[n];
    }
};

跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

class Solution {
public:
    /*
    简单的dp
    对于本题,青蛙一次可以跳1或2阶。
    令f(n)为青蛙跳n个台阶的跳法，则可推理出以下
        1、假定第一次跳的是1阶，那么剩下的是n-1个台阶，跳法是f(n-1);
        2、假定第一次跳的是2阶，那么剩下的是n-2个台阶，跳法是f(n-2)
        3、因此n阶的跳法为f(n) = f(n-1) + f(n-2) 
        4、又因为只有一阶的时候 f(1) = 1只有两阶的时候可以有 f(2) = 2
     发现最终得出的是一个斐波那契数列：
                  | 1, (n=1)
            f(n) =| 2, (n=2)
                  | f(n-1)+f(n-2) ,(n>2,n为整数)
    */
    int jumpFloor(int number) {
        if(number <= 0)//防御性编程
            return 0;
        if(number == 1)//1级台阶
            return 1;
        if(number == 2)//2级台阶
            return 2;

        int firstNum = 1;//n级台阶
        int secondNum = 2;
        int result;
        for(int i = 3 ; i <= number ; i++){
            result  = firstNum + secondNum;
            firstNum = secondNum;
            secondNum = result;
        }
        return result;
    }
};

变态跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

class Solution {
public:
    /*
    思路： 
    用f(n)表示n阶的跳法。
    2) f(0) = 0;
    2）f(1) = 1
    3) n=2时，第一次会有两个跳得方式：
                    第一次1阶，剩余f(1)
                    第一次2阶，剩余f(0)
        f(2) =  f(1) + f(0);
    4) n=3时，第一次会有三个跳得方式：
                    第一次1阶，剩余f(2)
                    第一次2阶，剩余f(1)
                    第一次3阶，剩余f(0)
         f(3) = f(2) + f(1) + f(0);
      因此结论是
      f(n) = f(0)+f(1)+f(2)+....+f(n-1)
      又因为
      f(n-1) = f(0)+f(1)+f(2)+...+f(n-1)
      所以
      f(n)-f(n-1) = f(n-1)  -> f(n) = 2*f(n-1)
      因此跳法为：
           | 0   ,    (n = 0) 
    f(n) = | 1   ,    (n = 1)
           | 2*f(n-1),(n >= 2)

     这种思路牛逼牛逼牛逼牛逼牛逼牛逼：
     每个台阶都有跳与不跳两种情况（除了最后一个台阶），最后一个台阶必须跳。所以共用2^(n-1)中情况。      
    */
    int jumpFloorII(int number) {
        if(number <= 0)
            return 0;
        if(number == 1)
            return 1;
        int preNum = 1;
        int result = 0;
        for(int i = 2 ; i <= number ; i++){
            result = 2 * preNum;
            preNum = result;
        }
        return result;
    }
};

矩形覆盖

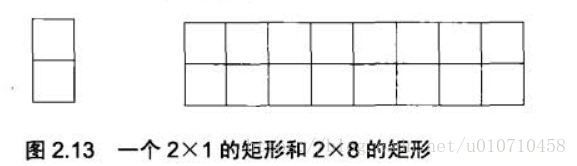
我们可以用2*1的小矩形横着或者竖着去覆盖更大的矩形。请问用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形，总共有多少种方法？

class Solution {
public:
    /*
    f(n)表示n个2*1的小矩形无重叠地覆盖一个2*n的大矩形覆盖的总方法数，则：
       1、f(1) = 1，只有竖1种。
       2、f(2) = 1+1，第一个横1种或第一个竖1种。
       3、f(3) = 1 + f(2)，第一个横1种，第一个竖剩余2*2，则为f(2)种
       4、f(4) = f(2) + f(3)，第一个横剩余2*2则f(2)种，第一个竖剩余3*3则f(3)种
       5、因此f(n) = f(n-1)+f(n-2),依次类推。
    */
    int rectCover(int number) {
        if(number <= 0)
            return 0;
        /*
        if(number == 1)
            return 1;
        if(number == 2)
            return 2;
        if(number == 3)
            return 3;
        */
        if(number <= 3)//前3种直接返回
            return number;

        //后续直接斐波那契数列实现
        int firstNum = 2;
        int secondNum = 3;
        int result;
        for(int i = 4; i<= number ; i++){
            result = firstNum + secondNum;
            firstNum = secondNum;
            secondNum = result;
        }
        return result;
    }
};

二进制中1的个数

输入一个整数，输出该数二进制表示中1的个数。其中负数用补码表示。

class Solution {
public:
    /*
     1、5- 0110  5-1= 0100  5&4 != 0 因此有一位
     或者通过flag每一位取试探。1<
     int  NumberOf1(int n) {
         int count = 0;
         while(n != 0){
             ++count;
             n = n&(n-1);//将最左边的一位清0
         }
         return count;
     }
};

扩展1：用一条语句判断一个整数是不是2的幂次方。
二进制数仅仅只有一个1，则直接使用return n&(n-1) == 0;
扩展2：输入两个整数m和n，计算需要改变m的二进制表示中的多少位才能得到n。
先异或，不同则为1，二进制中1的个数就是需要改变的个数。然后再求以后中1的个数。

数值的整数次方

给定一个double类型的浮点数base和int类型的整数exponent。求base的exponent次方。

#include
#define ABS(x)  ((x) > 0 ? (x) : -(x))
//返回一个数的绝对值,注意外层的括号一定得要，因为条件判断宏展开很可能出问题
//浮点数判断大小，因为浮点数精度的问题，判断两个浮点数是否相等就需要做差绝对值小于一定范围。
class Solution {
public:
    /*
    1、base=0 , 指数小于0无意义。
    2、base!=0 , exp为正负数的情况。
    */
    bool g_InvalidInput = false;
    double Power(double base, int exponent) {
        //return pow(base , exponent);
        double result = 1.0;
        if( ABS(base-0.0) < 0.000001  && exponent < 0){
            g_InvalidInput = true;
            return 0.0;
        }
        if(exponent  == 0)
            return 1;
        if(exponent  > 0){
            for(int i = 0; i < exponent ; i++)
                result *= base;
            return result;
        }else{
             for(int i = 0; i < ABS(exponent) ; i++)
                result *= base;
            return 1/result;
        }
    }
};

调整数组顺序使奇数位于偶数前面

输入一个整数数组，实现一个函数来调整该数组中数字的顺序，使得所有的奇数位于数组的前半部分，所有的偶数位于位于数组的后半部分，并保证奇数和奇数，偶数和偶数之间的相对位置不变。

class Solution {
public:
    //判断奇偶数，通过与1位于即可，很方便的。array[i]&1
    void reOrderArray(vector<int> &array) {
        vector<int> odd;//奇数
        vector<int> even;//偶数

        for(int i = 0 ; i < array.size() ; i++){
            if(array[i]&1 != 0) //奇数
                odd.push_back(array[i]);
            else                //偶数
                even.push_back(array[i]);
        }
        for(auto ite = even.begin() ;ite != even.end() ; ite++ )
            odd.push_back(*ite);
        for(int i = 0 ;i < array.size() ; i++ )
            array[i] = odd[i];
    }
};

链表中倒数第k个节点，从1开始判断

输入一个链表，输出该链表中倒数第k个结点。

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
            val(x), next(NULL) {
    }
};*/
class Solution {
public:
    /*
    1、k为0，必须防御。
    2、k为负数，将是一个非常大的正数，也必须防御。
    3、使用快慢指针，仅仅需要遍历一次链表即可。
    4、相关的单链表的题目： 求链表的中间节点？  判断链表是否有环？
    */
    ListNode* FindKthToTail(ListNode* pListHead , unsigned int k) {
        if(k == 0 || pListHead == NULL)//防御性编程
            return NULL;

        /* 1、2、3需要遍历两次链表，下面将通过快慢指针实现遍历一次链表的方法。
        ListNode* pHead = pListHead;
        int listLength = 0;
        //1、求出链表长度
        while(pHead != NULL){
            listLength++;
            pHead = pHead->next;
        }

        //2、比链表都长，错误
        if(k > listLength)
            return NULL;

        //3、倒数第k个，那么就是顺数第 listLength - k + 1个
        int kk = listLength - k;
        while(kk--){
            pListHead = pListHead->next;
        }
        return pListHead;

        */
        /*
          快慢指针，遍历一次并判断k是否大了，快先走k-1步这种方法直接画图判断临界点。
          仔仔细细仔细画图。
        */
        ListNode *pFast = pListHead;
        ListNode *pSlow = pListHead;
        for(int i = 0 ; i < k-1 ; i++){//pFast先走k-1步
            if(pFast->next != NULL)
                pFast = pFast->next;
            else
                return NULL;//如果直接pFast为空了，那么k大了，直接返回
        }
        while(pFast->next != NULL){
            pFast = pFast->next;
            pSlow = pSlow->next;
        }
        return pSlow;

    }
};

反转链表

输入一个链表，反转链表后，输出新链表的表头。

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
            val(x), next(NULL) {
    }
};*/
class Solution {
public:
    /*
    1、通过preNode记录前一个节点指针
    2、通过遍历一遍链表即可。仔细画图，在遍历的过程中保存上一个和下一个节点即可
    3、注意防御性编程.
    */
    ListNode* ReverseList(ListNode* pHead) {
        if(pHead == NULL)//防御传入空
            return NULL;
        if(pHead->next == NULL)//防御仅仅有一个节点
            return pHead;
        ListNode *preNode = NULL;
        ListNode *curNode = pHead;
        ListNode *tempNode = pHead;
        while(curNode != NULL){
            tempNode = curNode->next;//保存下一个节点地址
            curNode->next = preNode;//将当前节点指向前一个节点
            preNode = curNode;//更新前一个节点
            curNode = tempNode;//更新当前节点
        }
        return preNode;
    }
};

合并两个排序的链表

输入两个单调递增的链表，输出两个链表合成后的链表，当然我们需要合成后的链表满足单调不减规则。

/*
struct ListNode {
    int val;
    struct ListNode *next;
    ListNode(int x) :
            val(x), next(NULL) {
    }
};*/
class Solution {
public:
    ListNode* Merge(ListNode* pHead1, ListNode* pHead2)
    {
     /*
     非递归版本认真画图
        //1、三个防御性编程。两个空链表，一个空链表都是属于特殊情况
        if(pHead1 == NULL && pHead2 == NULL)
            return NULL;
        if(pHead1 == NULL && pHead2 != NULL)
            return pHead2;
        if(pHead1 != NULL && pHead2 == NULL)
            return pHead1;

        //2、开始两个链表合并
        ListNode *resultpHead;//保存合并头结点
        ListNode *resultpTemp;//临时节点

        //3、找出头结点
        if(pHead1->val < pHead2->val){
            resultpHead = pHead1;
            pHead1 = pHead1->next;
        }
        else{
            resultpHead = pHead2;
            pHead2 = pHead2->next;
        }
        resultpTemp = resultpHead;

        while(pHead1 != NULL || pHead2 != NULL){
            //总有一个链表先空，则直接返回第二个链表即可
            if(pHead1 == NULL){
                resultpTemp->next = pHead2;
                break;
            }
            if(pHead2 == NULL){
                resultpTemp->next = pHead1;
                break;
            }
            //判断节点大小，然后添加节点
            if(pHead1->val < pHead2->val){
                resultpTemp->next = pHead1;//插入节点
                resultpTemp = pHead1;//更新节点
                pHead1 = pHead1->next;//第一个链表指针指向下一个
            }
            else{
                resultpTemp->next = pHead2;//插入节点
                resultpTemp = pHead2;//更新节点
                pHead2 = pHead2->next;//第二个链表指向下一个
            }
        }
        return resultpHead;
        */
        /*
        递归版本，思路比较一个，整理节点，然后继续递归下去。
        */
        if(pHead1 == NULL && pHead2 == NULL)
            return NULL;
        if(pHead1 == NULL && pHead2 != NULL)
            return pHead2;
        if(pHead1 != NULL && pHead2 == NULL)
            return pHead1;
        //进入栈，直接整理好排序的链表
        ListNode *resultpHead = NULL;
       if(pHead1->val <= pHead2->val){
            resultpHead = pHead1;
            pHead1->next = Merge(pHead1->next, pHead2);
       }else{
            resultpHead = pHead2;
            pHead2->next = Merge(pHead1, pHead2->next);
       }
        return resultpHead;
    }

};

树的子结构

输入两棵二叉树A，B，判断B是不是A的子结构。（ps：我们约定空树不是任意一个树的子结构）

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
class Solution {
public:
    /*
    两个前序遍历，将节点压入vector，然后判断连续数字序列即可，这个方法比较慢，效果很不好的哦。
    vector<int> T1 , T2;
    bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
    {
        //注意下述防御性编程的理解。
        if(pRoot1 != NULL && pRoot2 != NULL){//任意一个为空，则为返回假
            PreOrder(pRoot1 , T1);//中序遍历起来
            PreOrder(pRoot2 , T2);//中序遍历起来
            if(T1.size() > T2.size()){
                for(int i = 0 ; i <= (T1.size()- T2.size()) ; i++){
                        for(int j = 0 ; j < T2.size() ; j++){//连续后面T2个是否相等？
                            if(T1[i+j] != T2[j])
                                break;
                            if(j == T2.size() -1)//成功找到
                                return true;
                        }
                    }
                return false;//没有找到
            }else
                return false;
        }else
            return false;

    }
    void PreOrder(TreeNode* pRoot , vector<int> &a){
        if(pRoot != NULL){
            a.push_back(pRoot->val);//前序遍历
            PreOrder(pRoot->left , a);
            PreOrder(pRoot->right , a);
        }
    }*/
    /*
    不需要全部遍历完，则分两步走：
    1、先找到A中和B根节点一样节点。
    2、从当前节点比较下去，直到树B为空为真
    */
    bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2)
    {
        //注意下述防御性编程的理解。
        bool result = false;
        if(pRoot1 != NULL && pRoot2 != NULL){//主循环是前序遍历，次循环也是前序遍历。
            if(pRoot1 ->val == pRoot2 ->val)//树A节点等于树B的根节点，那么可以继续玩下去了，否则继续遍历树A
                result = If_tree1_have_tree2(pRoot1 , pRoot2);//继续找下去
            if(result == false)//写出让别人容易看懂的代码，取消难以看懂的地方，尽量简单的写，类似Redis的作者，代码简答又有逻辑。
                result = HasSubtree(pRoot1->left , pRoot2);//递归左子树
            if(result == false)
                result = HasSubtree(pRoot1->right , pRoot2);//递归右子树
        }
        return result;
    }
    bool If_tree1_have_tree2(TreeNode* pRoot1, TreeNode* pRoot2){//递归找到下面的是不是子树

        if(pRoot2 == NULL)//可以递归找到树B为空，那么肯定是其子树
            return true;
        if(pRoot1 == NULL)//找到树A为空，则必定不是子树
            return false;
        if(pRoot1 ->val != pRoot2 ->val)//找的中途结束
            return false;

        //再对比树A和B左节点  然后比较树A和树B的右节点，一直比下去。
        return If_tree1_have_tree2(pRoot1->left , pRoot2->left) && 
               If_tree1_have_tree2(pRoot1->right , pRoot2->right);//利用短路特性。
    }
};

二叉树镜像

操作给定的二叉树，将其变换为源二叉树的镜像。
输入描述:

二叉树的镜像定义：源二叉树
            8
           /  \
          6   10
         / \  / \
        5  7 9 11
        镜像二叉树
            8
           /  \
          10   6
         / \  / \
        11 9 7  5

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
//二叉树镜像的递归及非递归实现
class Solution {
public:
    void Mirror(TreeNode *pRoot) {
        if(pRoot == NULL)//空树返回
            return;
        stack<TreeNode*> stackNode;//栈用来保存节点
        stackNode.push(pRoot);
        while( stackNode.size() ){
            TreeNode* tree = stackNode.top();//读取节点
            stackNode.pop();//弹出
            if(tree->left != NULL || tree->right != NULL){//交换左右节点
                TreeNode *ptemp = tree->left;
                tree->left = tree->right;
                tree->right = ptemp;
            }
            //然后重复操作
            if(tree->left)//左子树非空
                stackNode.push(tree->left);//左节点压栈
            if(tree->right)
                stackNode.push(tree->right);//右节点压栈
        }
    }
    /*前序遍历一次，则可以解决问题
        void Mirror(TreeNode *pRoot) {
            if(pRoot == NULL)
                return ;
            if(pRoot->left != NULL || pRoot->right != NULL){
                TreeNode *ptemp = pRoot->left;
                pRoot->left = pRoot->right;
                pRoot->right = ptemp;
            }
            if(pRoot->left != NULL)
                Mirror(pRoot->left);
            if(pRoot->right != NULL)
            Mirror(pRoot->right);                
        }    
    */
};

顺时针打印矩阵

输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字，例如，如果输入如下矩阵： 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 则依次打印出数字1,2,3,4,8,12,16,15,14,13,9,5,6,7,11,10.

class Solution {
public:
    vector<int> printMatrix(vector<vector<int> > matrix) {
        vector<int>res;
        res.clear();
        int row=matrix.size();//行数
        int columns=matrix[0].size();//列数
        //计算打印的圈数
        int circle=( (row < columns ? row : columns) - 1 ) / 2 + 1;//圈数
        for(int i=0;i//从左向右打印
            for(int j=i;j//从上往下的每一列数据
            for(int k=i+1;k1-i]);
            //判断是否会重复打印(从右向左的每行数据)
            for(int m=columns-i-2;(m>=i)&&(row-i-1!=i);m--)
                res.push_back(matrix[row-i-1][m]);
            //判断是否会重复打印(从下往上的每一列数据)
            for(int n=row-i-2;(n>i)&&(columns-i-1!=i);n--)
                res.push_back(matrix[n][i]);
        }
        return res;
    }
};

包含min函数的栈

定义栈的数据结构，请在该类型中实现一个能够得到栈中所含最小元素的min函数。

#include 
class Solution {
public:
    /*
    看到这个问题, 我们最开始可能会想, 添加一个成员变量用于保存最小元素, 每次压栈时如果压栈元素比当前最小元素更小, 就更新最小元素. 
    但是这样会有一个问题, 如果最小元素被弹出了呢, 如何获得下一个最小元素呢? 分析到这里可以发现, 
    仅仅添加一个成员变量存放最小元素是不够的, 我们需要在最小元素弹出后还能得到次小元素, 次小的弹出后, 还要能得到次次小的. 
    因此, 用另一个栈来保存这些元素是再合适不过的了. 我们叫它最小元素栈. 
    1、每次压栈操作时, 如果压栈元素比当前最小元素更小, 就把这个元素压入最小元素栈, 原本的最小元素就成了次小元素.. 
    2、弹栈时,如果弹出的元素和最小元素栈的栈顶元素相等, 就把最小元素的栈顶弹出.
    */
    stack<int> data;
    stack<int> aux;
    void push(int value) {
        data.push(value);
        if(aux.empty())
            aux.push(value);
        else if(aux.top() > value )//比最小值还小，则压栈
            aux.push(value);
    }
    void pop() {
        if(data.top() == aux.top())
            aux.pop();
        data.pop();
    }
    int top() {
        return data.top();
    }
    int min() {
        return aux.top();
    }
};

栈的压入和弹出序列

输入两个整数序列，第一个序列表示栈的压入顺序，请判断第二个序列是否为该栈的弹出顺序。假设压入栈的所有数字均不相等。例如序列1,2,3,4,5是某栈的压入顺序，序列4,5,3,2,1是该压栈序列对应的一个弹出序列，但4,3,5,1,2就不可能是该压栈序列的弹出序列。（注意：这两个序列的长度是相等的）。

class Solution {
public:
    /*
    模拟堆栈操作：将原数列依次压入辅助栈，栈顶元素与所给出栈队列相比，如果相同则出栈，
        1、如果不同则继续压栈，直到原数列中所有数字压栈完毕。
        2、检测栈中是否为空，若空，说明出栈队列可由原数列进行栈操作得到。否则，说明出栈队列不能由原数列进行栈操作得到。
    */
    bool IsPopOrder(vector<int> pushV,vector<int> popV) {
        if(pushV.size() == 0 || popV.size() == 0 || pushV.size() != popV.size())//注意防御性编程
            return false;
        stack<int> aux;
        int j = 0;
        for(int i = 0 ; i < pushV.size() ; i++){
            aux.push(pushV[i]);//将数据压栈
            while(!aux.empty() && aux.top() == popV[j]){
                aux.pop();
                ++j;
            }
        }
        return aux.empty();
    }
};

从上往下打印二叉树

从上往下打印出二叉树的每个节点，同层节点从左至右打印。

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
class Solution {
public:
    /*
    通过队列实现二叉树的层序遍历，广度优先遍历
    queue内部函数
        1、front back empty size（访问头和尾部 大小 空） 
        2、push pop（压入和弹出） 
    */
    vector<int> PrintFromTopToBottom(TreeNode* root) {
        queue treeQueue;
        vector<int> res;
        if(root == NULL)
            return res;
        treeQueue.push(root);
        while(!treeQueue.empty()){
            TreeNode *tempNode = treeQueue.front();
            treeQueue.pop();
            res.push_back(tempNode->val);
            if(tempNode->left != NULL)
                treeQueue.push(tempNode->left);
            if(tempNode->right != NULL)
                treeQueue.push(tempNode->right);
        }
        return res;
    }
};

二叉搜索树的后序遍历序列

题目描述
输入一个整数数组，判断该数组是不是某二叉搜索树的后序遍历的结果。如果是则输出Yes,否则输出No。假设输入的数组的任意两个数字都互不相同。

class Solution {
public:

/*
    思路：
    已知条件：后序序列最后一个值为root；二叉搜索树左子树值都比root小，右子树值都比root大。
    1、确定root；
    2、遍历序列（除去root结点），找到第一个大于root的位置，则该位置左边为左子树，右边为右子树；
    3、遍历右子树，若发现有小于root的值，则直接返回false；
    4、分别判断左子树和右子树是否仍是二叉搜索树（即递归步骤1、2、3）。
*/
    bool VerifySquenceOfBST(vector<int> sequence) {
        vector<int> leftTree,rightTree;
        int length = sequence.size();//序列长度
        if(length == 0)//小于1，则直接返回假
            return false;
        int root = sequence[length-1];//根节点
        int i = 0;
        for( ; i < length-1 ; i++){//找到第一个大于根节点的值
            if(sequence[i] > root)
                break;
        }
        for(int j = i ; j < length - 1 ; j++){//后面肯定是右子树,如果某个小于root，则返回假
            if(sequence[j] < root)
                return false;
        }
        //直接通过i切分左右子树
        for(int m = 0 ; m < i ; m++)
            leftTree.push_back(sequence[m]);//如果右子树节点大于2
        for(int m = i ; m < length - 1 ; m++)
            rightTree.push_back(sequence[m]);

        bool left = true , right = true;//树节点

        //一个或者0个节点则不必判断。
        if(leftTree.size() > 1) left = VerifySquenceOfBST(leftTree);//判断左子树
        if(rightTree.size() > 1) right = VerifySquenceOfBST(rightTree);//判断右子树
        return left && right;//验证左右子树全为真
    }
};

二叉树中和为某一值的路径

题目描述
输入一颗二叉树的跟节点和一个整数，打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。(注意: 在返回值的list中，数组长度大的数组靠前)。

class Solution {
public:
    /*
    明白前序遍历的过程
    1、用一个栈，记录前序遍历的节点，每次求其和，如果是子节点并且和为目标值，则打印路径。
    2、如果到达子节点并且不是目标值，则将栈顶节点弹出，继续寻找上一节点。
    3、每次递归都将目标值减去当前节点值，如果最后节点节点满足要求，那么节点必定和递归传入的值相等。
    */
    vector<int> path;       //记录一条路径
    vector<vector<int>> res;//记录全部符合条件的路径
    vector<vector<int> > FindPath(TreeNode* root,int expectNumber) {
        if(root == NULL)
            return res;
        findPath(root , expectNumber);//寻找路径
        return res;
    }
    void findPath(TreeNode* root , int sum){//中序遍历
        if(root == NULL)//递归结束标志
            return;
        path.push_back(root->val);//当前数据压栈
        if(!root->left && !root->right && sum == root->val)//如果当前是子节点，且递归传入的值和当前节点值一样，那么是一条路径
            res.push_back(path);
        if(root->left)
            findPath(root->left , sum - root->val);
        if(root->right)
            findPath(root->right , sum - root->val);
        path.pop_back();//子节点不是值，则将最后节点弹出，重新遍历
    }
};

复杂链表的复制

题目描述
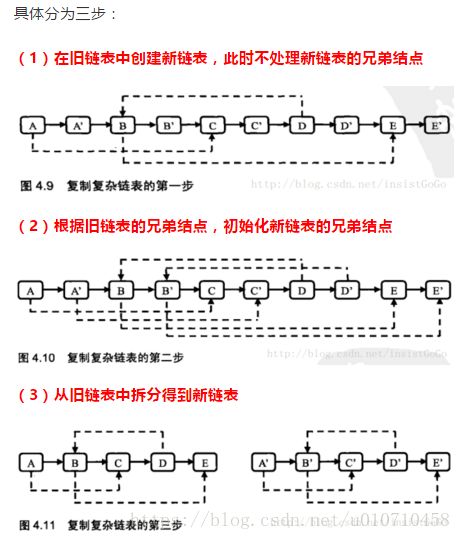
输入一个复杂链表（每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针指向任意一个节点），返回结果为复制后复杂链表的head。（注意，输出结果中请不要返回参数中的节点引用，否则判题程序会直接返回空）

/*
struct RandomListNode {
    int label;
    struct RandomListNode *next, *random;
    RandomListNode(int x) :
            label(x), next(NULL), random(NULL) {
    }
};
*/
class Solution {
public:
    RandomListNode* Clone(RandomListNode* pHead)
    {
        if(pHead == NULL)
            return NULL;
         RandomListNode *pCur = pHead;

        //复杂链表节点的复制 插入节点即可 A->B->C  A->A'->B->B'-C-C'
        while(pCur != NULL){
            RandomListNode *newNode = new RandomListNode(pCur->label);
            newNode->next = pCur->next;
            pCur->next = newNode;
            pCur = newNode->next;//指向原来的下一个节点
        }
       //复制random
        pCur = pHead;
        while(pCur != NULL){
            if(pCur->random != NULL)//修改成下一个节点
                pCur->next->random = pCur->random->next;
            pCur = pCur->next->next;//前进两步
        }
        //查分链表 选择偶数序号
        pCur = pHead;
        RandomListNode *pCloneHead = pHead->next;
        RandomListNode *temp = NULL;
        while(pCur->next != NULL){//插入奇数链表即为所得  这里最牛逼，每次仅仅修改一个节点即可。
            temp = pCur->next;//暂存下一个节点
            pCur->next = temp->next;
            pCur = temp;
        }
        return pCloneHead;
    }
};

数组中出现次数超过一半的数字

题目描述：
数组中有一个数字出现的次数超过数组长度的一半，请找出这个数字。例如输入一个长度为9的数组{1,2,3,2,2,2,5,4,2}。由于数字2在数组中出现了5次，超过数组长度的一半，因此输出2。如果不存在则输出0。

本题以及下面这题全部都可以通过快速排序的算法实现，复杂度都是O（N）。

/*
特点：数组中有一个数字出现的次数超过了数组长度的一半。如果把这个数组排序，
     那么排序之后位于数组中间的数字一定就是那个出现次数超过数组一半的数字，
     可以通过反证法证明，如果数字不在中间，那么不论在哪来都不可能超过一半
*/
//从数组中选取一个数，比其小的放到左边，比其大的放到右边，并返回切分元素的索引
//length为数组长度， start 数组开始索引 ， end数组结束索引
void exch(int *data , int i , int j)
{
    int temp = data[i];
    data[i] = data[j];
    data[j] = temp;
}
/*
切分原则：随机选取某个数v，然后经过切分后 
                            左边都小于等于v
                            右边都大于v
*/
int Partition(int *data , int start , int end)
{
    int i = start , j = end + 1;
    int v = data[i];//用来切分数组的元素
    while(1){//找到切分的位置，并交互其他位置  左边小于等于v
        while( data[++i] < v)//扫描左边直到比v大停止
            if(i == end)
                break;
        while( v <= data[--j] )//扫描右边直到比v小停止  右边必须
            if(j == start)
                break;
        if(i >= j)//检查是否指针i和j交叉，如果有交叉，则停止继续搜索
            break;
        exch(data , i , j);//交互
    }
    exch(data , start , j);//交换最后切分元素
    return j;//返回切分元素的索引
}

//通过切分找到中间的位置索引即可，如果某个数组有个数大于一半则必定在中间，反之不成立，因此需要判断。
bool IsInvalidInput = false;
int MoreThanHalfNum_Solution(int *numbers , int length) {
    if(length <= 0)//防御性编程
        return 0;
    int middle = length /2;
    int start = 0;
    int end = length - 1;
    int index = Partition(numbers , start , end);
   while(index != middle){
        if(index > middle)//在index的左边
            index = Partition(numbers , start , index - 1);
        else//在index的的右边
            index = Partition(numbers , index+1 , end);
   }
   //到此找到了中间大小数字
   int res = numbers[index];

   //判断是不是确实大于一半
   int times = 0;
   for(int i = 0 ; i if(numbers[i] == res)
           times++;
   }
   if(2*times <= length){
       res = 0;
       IsInvalidInput  = true;
   }
   return res;
}

//切分实现了快速排序
void quicksort(int *number , int start , int end)//快速排序
{
    if(start >= end)//递归退出
        return ;
    int index = Partition(number , start , end);
    quicksort(number , start , index -1);//左半部分排序，继续切分
    quicksort(number , index+1 , end);   //右半部分排序，继续切分
}

最小的k个数或最大k个数

题目描述：
输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4。

/*
  1、同理通过切分思路去做，如果返回的index是k-1，则最小的k个数就是包括k-1在内的左边数据
  2、一直切分，直到k-1即可
*/
void getLeastNumbers(int *numbers , int length , int *output , int k)
{
    if(length <= 0)//防御性编程
        return ;
    if(length <= k)
        return ;
    int start = 0;
    int end = length - 1;
    int index = Partition(numbers , start , end);
    //{2,4,4,7,4,9,4,5,4}
    while(index != k-1){
        if(index > k-1)//在index的左边
            index = Partition(numbers , start , index - 1);
        else//在index的的右边
            index = Partition(numbers , index+1 , end);
    }
    for(int i = 0; i < k ; i++){
        output[i] = numbers[i];
    }
}

2、对于k个最大数，可以使用最小堆。堆顶最小，每次来个值和最小比较比其小则舍弃，大则堆顶弹出并push进堆
   对于k个最小数，可以使用最大堆，类似的做法

字符串的全排列

题目描述
输入一个字符串,按字典序打印出该字符串中字符的所有排列。例如输入字符串abc,则打印出由字符a,b,c所能排列出来的所有字符串abc,acb,bac,bca,cab和cba。（可能出现重复字符串，因此需要防止重复）
https://blog.csdn.net/x526967803/article/details/77718434

/* Function to swap values at two pointers */
void swap(char *a, int i , int j)
{
    char temp;
    temp = a[i];
    a[i] = a[j];
    a[j] = temp;
}
//字符串第一个字符索引t，最后一个字符索引r
void backtrack(char *a, int t, int r)
{
   if (t >= r)
     printf("%s\n", a);
   else
   {
       for (int i = t; i <= r; i++)//全排列因为有r-t+1层
       {
          if(i != t && a[i] == a[t])//去除重复字符串
              continue;
          swap(a , t , i);
          backtrack(a , t+1 , r);
          swap(a , t , i); //backtrack
       }
   }
}

字符串的全组合（位）

char str[] = "abcde";//0 0 0 0 0 通过位运算表示
void print_subset(int n , int s)// 判断数s的0-n位是否为0
{
    for(int i = 0 ; i < n ; ++i)
    {
        //第0 1 2 3 n-1 位是否位0，即可打印数字
        if( s & (1<// 判断s的二进制中哪些位为1，即代表取某一位
            printf("%c ",str[i]);   //或者a[i]
    }
    printf("\n");
}
void subset(int n)
{
    //最大数位2^n -1  也就是循环(i < 2^n)
    for(int i= 0 ; i < (1<

数组中只出现一次的数字

题目描述
一个整型数组里除了两个数字之外，其他的数字都出现了偶数次。请写程序找出这两个只出现一次的数字。
思路是完全采用异或，先异或，根据结果中首次出现某位为1的位置，来将数组区分为两组，然后再分别异或。

class Solution {
public:
    /*
    1、任何数字异或本身都为0，任何数字与0异或都为本身，所以假如只有一个数字不一样，那么
       数组中每个数字异或必定为那个仅仅出现一次的数字。
    2、现在有两个数字，可以尝试着将数组区分出两个子数组，并且每个数组中仅仅包含一起出现一次的数字
       其余都是成对出现。同样异或，依据异或结果数组第一个1的位置，来区分两个数组
    */
    void FindNumsAppearOnce(vector<int> data,int* num1,int *num2) {
        int length = data.size();
        if(length < 2)//防御性编程，如果小于2，则直接返回嘛
            return ;
        int temp = 0;//存储异或结果
        for(int i  = 0 ; i < length ; i++)
            temp ^= data[i];
        int indexBit = 0;
        while( !(temp & (1<//找到第一个为1的索引,通过数组元素第indexBit是否为1分为两组
            indexBit++;
        int numb1 = 0;
        int numb2 = 0;
        for(int i = 0 ; i < length ; i++){//分两组存储异或结果
            if( data[i] & (1<else
                numb2 ^= data[i];
        }
        *num1 = numb1;
        *num2 = numb2;
    }
};

//下面写法比自己的好
class Solution {
public:
    //思路：用异或的特性，A^A=0 0^X=X;以及异或的交换律特性。
    void FindNumsAppearOnce(vector<int> data,int* num1,int *num2) {
        int x=0,len=data.size();
        for(int i=0;i//x保存所有元素异或的结果
        int n=1;
        while((x & n)==0)//找出最右边第1个不为0的位置
            n=n<<1;
        int x1=0,x2=0;
        for(int i=0;iif(data[i] & n)//根据第一个不为0的位置重新将数组进行划分
                x1^=data[i];
            else
                x2^=data[i];
        *num1=x1;
        *num2=x2;
        return ;
    }
};

二叉树的下一个结点

题目描述
给定一个二叉树和其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树中的结点不仅包含左右子结点，同时包含指向父结点的指针。

/*
struct TreeLinkNode {
    int val;
    struct TreeLinkNode *left;
    struct TreeLinkNode *right;
    struct TreeLinkNode *next;
    TreeLinkNode(int x) :val(x), left(NULL), right(NULL), next(NULL) {

    }
};
*/
class Solution {
public:
    /*
    画图，然后加上理解有以下三种情况：
    1、给出的节点为空，则返回空；
    2、节点右孩子存在，则设置一个指针从该节点的右孩子出发，一直沿着指向左子结点的指针找到的叶子节点即为下一个节点；
    3、如果右孩子不存在且节点不是根节点。如果该节点是其父节点的左孩子，则返回父节点；否则继续向上遍历其父节点的父节点，重复之前的判断，
       返回结果。
    */
    TreeLinkNode* GetNext(TreeLinkNode* pNode)
    {
        if(pNode == NULL)//case 1
            return NULL;
        if(pNode->right != NULL){//case 2
            TreeLinkNode *temp;
            temp = pNode->right;
            while(temp->left != NULL)//找到左子节点
                temp = temp->left;
            return temp;
        }
        while(pNode->next != NULL){//case 3 循环找其父节点，其是否是其父节点的左子树，如果没有，那就返回空即可，就这三种情况
            TreeLinkNode *temp = pNode->next;//父节点
            if(temp->left == pNode)
                return temp;
            else
                pNode = pNode->next;
        }
        return NULL;
    }
};

连续子数组的最大和（必考）

HZ偶尔会拿些专业问题来忽悠那些非计算机专业的同学。今天测试组开完会后,他又发话了:在古老的一维模式识别中,常常需要计算连续子向量的最大和,当向量全为正数的时候,问题很好解决。但是,如果向量中包含负数,是否应该包含某个负数,并期望旁边的正数会弥补它呢？例如:{6,-3,-2,7,-15,1,2,2},连续子向量的最大和为8(从第0个开始,到第3个为止)。给一个数组，返回它的最大连续子序列的和，你会不会被他忽悠住？(子向量的长度至少是1)

class Solution {
public:
    /*
    使用动态规划
    F(i)表示array[i]为末尾元素的子数组的和的最大值，子数组的元素的相对位置不变
    F(i)=max（F(i+1)+array[i],array[i]）
    */
    int FindGreatestSumOfSubArray(vector<int> array) {
        if(array.empty()){
            return 0;
        }
        int greatestSumStart = 0;
        int Fi = array[0];
        int MaxFi = 0x80000000;//最小的负数
        //动态规划求解
        for(int i = 1 ; i < array.size() ; i++){
            if(Fi <= 0){
                Fi = array[i];
                greatestSumStart = i;//记录开始索引
            }
            else
                Fi = Fi + array[i];
            if(Fi > MaxFi)//更新最大Fi
                MaxFi = Fi;
        }
        return MaxFi;
    }
};

对称的二叉树（必考）

题目描述
请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。
通过递归实现

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
/*

            8
           /  \
          2   2
         / \  / \
        4  3 3   4
上述是一颗对称二叉树。总结：
1、根节点以及其左右子树数据相同
2、左子树的左子树和右子树的右子树数值相同
3、左子树的右子树和右子树的左子树数值相同

*/
class Solution {
public:
    bool isSymmetrical(TreeNode* pRoot)
    {
        if(pRoot == NULL){
            return true;
        }
        return comRoot(pRoot->left, pRoot->right);//从根的左右子树开始
    }
private: 
    //如果对称，则返回真。
    bool comRoot(TreeNode* left, TreeNode* right) {
        if(left == NULL && right == NULL)//左右都为空，返回真。直接返回，这层对称
            return true;
        if( (left == NULL && right != NULL) || (left != NULL && right == NULL) )//一个为空，一个不为空，返回假，直接返回，非对称
            return false;
        //全部不为空，则比较数值
        if(left->val != right->val)//不等，直接返回，非对称 
            return false;
        return comRoot(left->right, right->left) && comRoot(left->left, right->right);//继续比较第2和3步
    }
};

按之字形顺序打印二叉树

题目描述
请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。
画图，然后通过两个栈实现即可，在过程中必须确保压栈的顺序是正确的才可以。
奇数层，则弹出数值，并将子节点从左到右压入偶数层，则后续出栈就是从右到左打印。
偶数层，则弹出数值，并将子节点从右到左压入奇数层，则后续出栈就是从左到右打印。

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
public:
    /*
    可以通过两个栈实现，画图画图。
    stack1存储奇数层节点，1 3 5 7
    stack2存储偶数层节点，2 4 6 8
    开始根节点入stack1.
    如果是奇数层，则先压入左节点进s2，再压入右节点入s2，再将数据加入vector，那么下层s2出栈的时候就是从右到左加入vector。
    如果是偶数层，则先压入右节点进s1，再压入左节点入s1，再将数据加入vector，那么下层s2出栈的时候就是从左到右加入vector。
    */
    vector<vector<int> > Print(TreeNode* pRoot) {
        vector<vector<int> > res;
        if(pRoot == NULL)
            return res;
        stack s1;
        s1.push(pRoot);//初始化s1
        stack s2;
        int layers = 1;
        while(!s1.empty() || !s2.empty()){//某个不为空
            if(layers%2 == 1){//奇数层
                vector<int> temp;
                while(!s1.empty()){//弹出全部s1，并加入vector，并加入s2全部对于节点
                    TreeNode *top = s1.top();
                    s1.pop();
                    if(top != NULL){
                        temp.push_back(top->val);
                        s2.push(top->left);
                        s2.push(top->right);
                    }
                }
                if(temp.size() != 0){
                    layers++;
                    res.push_back(temp);
                }
            }else{//偶数层
                vector<int> temp;
                while(!s2.empty()){//弹出全部s2，并将数值加入vector，并加入s1全部对于节点
                    TreeNode *top = s2.top();
                    s2.pop();
                    if(top != NULL){
                        temp.push_back(top->val);
                        s1.push(top->right);
                        s1.push(top->left);
                    }
                }
                if(temp.size() != 0){
                    layers++;
                    res.push_back(temp);
                }
            }
        }
        return res;
    }
};

把二叉树打印成多行

题目描述
从上到下按层打印二叉树，同一层结点从左至右输出。每一层输出一行。
通过队列实现层序遍历。

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};
*/
class Solution {
public:
    //牛客网第一个数字说明了错误在哪一行，第二个数字说明的错误的类型。
    /*
    层序遍历二叉树(广度优先遍历)，一个队列即可搞定，
       每次连续弹出一层的节点，而不是一个一个的弹出，这样就可以实现打印成多行了。
    */
        vector<vector<int> > Print(TreeNode* pRoot) {
            vector<vector<int>> res;
            if(pRoot == NULL)//防御性编程
                return res;
            queue q;
            q.push(pRoot);
            while(!q.empty()){//队列非空，则一直继续
                vector<int> tempRes;
                int qSize  = q.size();//记录当前层 入队的点数
                for(int i = 0 ; i < qSize; i++){
                    TreeNode *temp = q.front();//每一轮会压入一层的节点
                    q.pop();
                    tempRes.push_back(temp->val);
                    if(temp->left != NULL)
                        q.push(temp->left);
                    if(temp->right != NULL) 
                        q.push(temp->right);
                }
                if(!tempRes.empty())
                    res.push_back(tempRes);
            }
            return res;
        }
};

序列化二叉树(少考太难)

题目描述
请实现两个函数，分别用来序列化和反序列化二叉树

class Solution {
public:
    /*
        1
       / \
      2   3
     / \  / \
    4  5  6  7 
    1、序列化：前序遍历，并且每个val后面加,每个空节点用#表示。例如上述序列化为"1,2,4##,5##,3,6##,7##"
    2、反序列化：从1中恢复二叉树。
    */
    char* Serialize(TreeNode *root) {    
        if(root == NULL)
            return NULL;
        string str;
        Serialize(root , str);//返回序列化的字符串
        char *res = (char *)malloc(str.length() + 1);
        int i = 0;
        for( ; i < str.length() ; i++)//赋值
            res[i] = str[i];
        res[i] = '\0';//结束符
        return res;//返回
    }
    //递归实现前序遍历
    void Serialize(TreeNode *root, string& str){
        if(root == NULL){
            str += '#';
            return ;
        }
        string r = to_string(root->val);//值变为字符串
        str += r;
        str += ',';
        Serialize(root->left, str);//左
        Serialize(root->right, str);//右
    }

    //解码前面的字符串
    TreeNode* Deserialize(char *str) {
        if(str == NULL)
            return NULL;
        TreeNode *ret = Deserialize(&str);
        return ret;
    }
    TreeNode* Deserialize(char **str){//由于递归时，会不断的向后读取字符串
        if(**str == '#'){  //所以一定要用**str,
            ++(*str);      //以保证得到递归后指针str指向未被读取的字符
            return NULL;
        }
        int num = 0;
        while(**str != '\0' && **str != ','){
            num = num*10 + ((**str) - '0');
            ++(*str);
        }
        TreeNode *root = new TreeNode(num);
        if(**str == '\0')
            return root;
        else
            (*str)++;
        root->left = Deserialize(str);
        root->right = Deserialize(str);
        return root;
    }
};

二叉搜索树的第k个结点（必考）

题目描述
给定一棵二叉搜索树，请找出其中的第k小的结点。例如， （5，3，7，2，4，6，8） 中，按结点数值大小顺序第三小结点的值为4。
中序遍历，递归与非递归实现。请背下来。

/*
            5
           /  \
          3    7
         / \  / \ 
        2  4 6   8
 第三个节点是4，注意没有第0个节点和负数节点。一定得注意边界条件的判定。       
*/
class Solution {
public:
    /*
    1、中序遍历的递归实现
    */
    vector<TreeNode*> a;
    int index = 0;
    TreeNode* KthNode(TreeNode* pRoot, int k)
    {
        if(pRoot != NULL){
            Order(pRoot);//中序遍历压入数组
            if(k > 0 && k <= a.size() )//防御性编程    
                return a[k-1];
            else
                return NULL;
        }
        return NULL;
    }
    void Order(TreeNode* pRoot){
        if(pRoot != NULL){
            Order(pRoot->left);
            a.push_back(pRoot);
            Order(pRoot->right);
        }
    }
    /*
    采用中序遍历的非递归形式，时间复杂度是O(k)

    TreeNode* KthNode(TreeNode* pRoot, int k)
    {
        int count = 0;
        stack<TreeNode*> Snode;//栈
        if(k <= 0)
            return NULL;
        while(pRoot != 0 || Snode.size() != 0){
            while(pRoot != NULL){//左子树全部入栈
                Snode.push(pRoot);
                pRoot = pRoot->left;
            }
            if(Snode.size() != 0){
                pRoot = Snode.top();
                if(++count == k)
                    return pRoot;
                Snode.pop();//出栈
                pRoot = pRoot->right;
            }
        }
        return NULL;//全部没有，则返回空，因为k比index还要大
    }*/
};

数据流中的中位数（难题可能考）

题目描述
如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排序之后中间两个数的平均值。我们使用Insert()方法读取数据流，使用GetMedian()方法获取当前读取数据的中位数。
方法在于使用两个堆，最大堆和最小堆，确保最大堆的数据小于等于最小堆即可。

class Solution {
public:
    /*
    画图可以的出下面结论：
    1、用一个最大堆和一个最小堆，维持大顶堆的数都小于等于小顶堆的数，
    2、始终维持两个堆中数据相等或者相差1，那么平均数必定都在两个堆顶。
    */
    priority_queue<int, vector<int>, less<int> > maxHeap;
    //less(father ， newData) 为真才互换位置，那么就是确保父节点大于等于两个子节点，所以是最大堆

    priority_queue<int, vector<int>, greater<int> > minHeap;
    //greater(father ， newData) 为真才互换位置，那么就是确保父节点小于等于两个子节点，所以是最小堆
    void Insert(int num)
    {
        //维持大根堆中的数都小于等于小根堆，仅仅比较堆顶元素即可
        if(maxHeap.empty() || num <= maxHeap.top())//这里比较切勿使用minHeap，会造成段错误，因为minHeap没有初始化。数字小于小根堆顶，则插入大根堆
            maxHeap.push(num);
        else
            minHeap.push(num);
        //后面两个if会将数据最后均衡起来，不会挂掉
        if(maxHeap.size() == minHeap.size() + 2){//偶数个元素则维持最大堆和最小堆元素相等
            minHeap.push(maxHeap.top());
            maxHeap.pop();
        }
        if(maxHeap.size() + 1 ==  minHeap.size()){//奇数个元素，则维持最大堆中元素多余最小堆一个。
            maxHeap.push(minHeap.top());
            minHeap.pop();
        }
    }
    double GetMedian()
    {
        if(maxHeap.size() == minHeap.size())//偶数个
            return (minHeap.top() + maxHeap.top())/2.0;//注意必须除2.0将转换成浮点数计算，很重要
        else//奇数个
            return maxHeap.top();
    }
};

滑动窗口的最大值

题目描述
给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。
注意两防御性编程，以及暴力解答的方法。十分明确的方法哦，必须知道这个问题。

/*
暴力解法，很简单，每次滑动一个窗口
 1 2 3 4 
*/
class Solution {
public:
    vector<int> maxInWindows(const vector<int>& num, unsigned int size)
    {
        int numLength = num.size();
        vector<int> res;
        int windows = numLength - size + 1;//总得滑动窗口数量
        if(size <= 0)//防御性编程，用户错误输入
            return res;
        if(size > numLength){//窗口太大,直接返回空即可
            return res;
        }
        for(int i = 0 ; i < windows ; i++){
            int max = num[i];
            for(int j = i+1 ; j < i + size ; j++){
                if(num[j] > max)
                    max = num[j];
            }
            res.push_back(max);
        }
        return res;
    }
};

机器人的运动范围

题目描述
地上有一个m行和n列的方格。一个机器人从坐标0,0的格子开始移动，每一次只能向左，右，上，下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于k的格子。 例如，当k为18时，机器人能够进入方格（35,37），因为3+5+3+7 = 18。但是，它不能进入方格（35,38），因为3+5+3+8 = 19。请问该机器人能够达到多少个格子？
递归解决问题。注意二维数组的内存分配的问题并清空的问题，很值得注意。
注意二维数组的分配是一个关键，通过分配一维数组，然后模拟二维数组的分配。

class Solution {
public:
    bool hasPath(char* matrix, int rows, int cols, char* str)
    {
        /*char **flag = (char **)malloc(sizeof(char *)*rows);//生成Flag标记
        for(int i = 0 ; i < rows ; i++){//内存分配并清0
            flag[i] = (char *)malloc(sizeof(char)*cols);
            memset(flag[i] , 0 , sizeof(char)*cols);
        }*/
        //这里完全可以用一维数字模拟二维数组的使用，使内存连续分配
        char *flag = (char *)malloc(sizeof(char)*rows*cols);//连续空间，仅仅需要按照二维访问即可
        memset(flag , 0 , rows*cols);
        //找到可能的每个字符开始，然后开始遍历，找到可能的一条路径即可
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (helper(matrix, rows, cols, i, j, str, 0, flag))
                    return true;
            }
        }
        return false;
    }
    //matrix 二维矩阵 rows行 cols列 i j分别对应当前位置  str表示目标字符 k表示第k个目标 flag标记是否被访问过
    bool helper(char *matrix, int rows, int cols, int i, int j, char *str, int k, char *flag) {
        int index = i * cols + j;//这是模拟二维数组的关键
        if (i < 0 || i >= rows || j < 0 || j >= cols || matrix[index] != str[k] || flag[index] == 1)
            return false;
        if(k == strlen(str) - 1) 
            return true;//比到最后一个字符
        flag[index] = 1;//标记为1
        if (helper(matrix, rows, cols, i - 1, j, str, k + 1, flag)        //左
            || helper(matrix, rows, cols, i + 1, j, str, k + 1, flag) //右
            || helper(matrix, rows, cols, i, j - 1, str, k + 1, flag) //上
            || helper(matrix, rows, cols, i, j + 1, str, k + 1, flag))//下 
        {
            return true;
        }
        flag[index] = 0;//回溯起来
        return false;
    }
};

数字在排序数组中出现的次数

题目描述
统计一个数字在排序数组中出现的次数。
看见有序，直接二分查找，明白了没有？

class Solution {
public:
    /*
    1、排序，则可以通过二分查找。 分别找到第一个索引和最后一个索引，想减即可。
    快速查找。  看见有序 肯定是二分查找，所以不需要惊慌。
    */
    int GetNumberOfK(vector<int> data ,int k) {
        int length = data.size();
        if(length == 0)
            return 0;
        int firstK = getFirstNum(data , k , 0 , length - 1);
        int lastK  = getLastNum(data , k , 0 , length - 1);
        if(firstK != -1 && lastK != -1)//同时找到，则返回次数,任何一个没有找到则返回0
            return lastK - firstK + 1;
        else 
            return 0;
    }
    //二分查找得到, 从小到大
    int getLastNum(vector<int> &data , int k ,int start , int end){
        int mid = (start+end)/2;
        int length = data.size();
        while(start <= end){
            if(data[mid] > k)
                end = mid - 1;
            else if(data[mid] < k)
                start = mid + 1;
            else if(mid + 1 < length && data[mid + 1] == k)//这句是找到最后一个的关键
                start = mid + 1;
            else
                return mid;
            mid = (start + end)/2;
        }
        return -1;//没有找到
    }
        //二分查找得到, 从小到大
    int getFirstNum(vector<int> &data , int k ,int start , int end){
        int mid = (start + end)/2;
        int length = data.size();
        while(start <= end){
            if(data[mid] > k)
                end = mid - 1;
            else if(data[mid] < k)
                start = mid + 1;
            else if(mid - 1 >= 0 && data[mid - 1] == k)//这句是找到最前一个的关键
                end = mid - 1;
            else
                return mid;
            mid = (start + end)/2;
        }
        return -1;//没有找到
    }
};

二叉树的深度

输入一棵二叉树，求该树的深度。从根结点到叶结点依次经过的结点（含根、叶结点）形成树的一条路径，最长路径的长度为树的深度。

/*
struct TreeNode {
    int val;
    struct TreeNode *left;
    struct TreeNode *right;
    TreeNode(int x) :
            val(x), left(NULL), right(NULL) {
    }
};*/
class Solution {
public:
    //最终返回某个节点的深度
    int TreeDepth(TreeNode* pRoot)
    {
        /*
        递归思路：
              一棵树只有一个节点，深度是1。树的深度等于其左、右子树深度的较大值+1。
        if(pRoot == NULL)//防御性编程实现
            return 0;
        int nLeft = TreeDepth(pRoot-> left);//左子树深度
        int nRight = TreeDepth(pRoot-> right);//右子树深度
        return (nLeft >　nRight) ? (nLeft + 1 ) : (nRight + 1);//比较，较大则加1。采用递归实现。
        */
    }
};

判断平衡二叉树

class Solution {
public:
    bool IsBalanced_Solution(TreeNode* pRoot) {
        /*
            遍历每个节点的时候，调用TreeDepth得到左右子树的高度。如果每个节点的深度不超过1，则是一颗平衡二叉树。
            因为TreeDepth函数，导致许多节点会被重复遍历
         if(pRoot == NULL)//节点没有左右子树，肯定平衡。
             return true;
        int left = TreeDepth(pRoot-> left);//返回左子树深度
        int right = TreeDepth(pRoot-> right);//返回右子树深度
        int diff = left - right;
        if(diff > 1 || diff < -1)//不能超过1
            return false;
        return IsBalanced_Solution(pRoot-> left) && IsBalanced_Solution(pRoot-> right);//继续
        */

        /*
        后序遍历的方式遍历整颗二叉树，在遍历某个节点的左右子节点后，根据左右子节点的深度判断是不是平衡。
        */
        int depth = 0;
        return IsBalanced(pRoot , &depth);
    }
    bool IsBalanced(TreeNode* pRoot , int *pDepth)
    {
        if(pRoot == NULL){
            *pDepth = 0;
            return true;
        }
        int left = 0 , right = 0;
        if( IsBalanced(pRoot-> left , &left) && IsBalanced(pRoot-> right , &right) ){//判断左右子树IsBalanced，并记录深度
            int diff = left - right;
            if(diff <= 1 && diff >= -1){
                *pDepth = 1 + (left > right ? left : right);
                return true;
            }
        }
        return false;
    }
    //返回某个节点的深度
    int TreeDepth(TreeNode* pRoot)
    {
        /*
        递归思路：
              一棵树只有一个节点，深度是1。树的深度等于其左、右子树深度的较大值+1。
        */
        if(pRoot == NULL)//防御性编程实现
            return 0;
        int nLeft = TreeDepth(pRoot-> left);//左子树深度
        int nRight = TreeDepth(pRoot-> right);//右子树深度
        return (nLeft >　nRight) ? (nLeft + 1 ) : (nRight + 1);//比较，较大则加1。采用递归实现。

    }
};

和为s的连续正数序列

小明很喜欢数学,有一天他在做数学作业时,要求计算出9~16的和,他马上就写出了正确答案是100。但是他并不满足于此,他在想究竟有多少种连续的正数序列的和为100(至少包括两个数)。没多久,他就得到另一组连续正数和为100的序列:18,19,20,21,22。现在把问题交给你,你能不能也很快的找出所有和为S的连续正数序列? Good Luck!

class Solution {
public:
    /*
用两个数字begin和end分别表示序列的最大值和最小值，
首先将begin初始化为1，end初始化为2.
如果从begin到end的和大于s，我们就从序列中去掉较小的值(即增大begin),相反，只需要增大end。
终止条件为：一直增加begin到(1+sum)/2为止。

上述方法叫做双指针技术，就是相当于有一个窗口，窗口的左右两边就是两个指针，
我们根据窗口内值之和来确定窗口的位置和宽度，滑动窗口方法。
    */
    vector< vector<int> > FindContinuousSequence(int sum) {
        vector<vector<int> > res;
        vector<int> a;
        if(sum < 3)//小于3，则没有连续正数
            return res;
        int small = 1;//初始化为1
        int big = 2;//初始化为2
        int total = small + big;
        while(small <= (sum-1)/2 ){//因为至少两个连续数字，所以small最大为(sum-1)/2
             if(total == sum){//如果相等，则压入，否则更新数据
                 for(int i = small ; i <= big ; i++)
                         a.push_back(i);
                 res.push_back(a);
                 a.clear();
                 total -= small++;//滑动窗口一下
             }else if(total < sum)//小于，则需要增加big
                 total += ++big;//++big 并更新连续和
             else //大于，则需要增加small
                 total -= small++;//small++ 并更新连续和
        }
        return res;
    }
    /*
    vector > FindContinuousSequence(int sum) {
        vector > allRes;
        int phigh = 2,plow = 1;

        while(phigh > plow){
            int cur = (phigh + plow) * (phigh - plow + 1) / 2;
            if( cur < sum)
                phigh++;

            if( cur == sum){
                vector res;
                for(int i = plow; i<=phigh; i++)
                    res.push_back(i);
                allRes.push_back(res);
                plow++;
            }

            if(cur > sum)
                plow++;
        }

        return allRes;
    }
    */
};

和为s的两个数

题目描述
输入一个递增排序的数组和一个数字S，在数组中查找两个数，使得他们的和正好是S，如果有多对数字的和等于S，输出两个数的乘积最小的。

class Solution {
public:
    vector<int> FindNumbersWithSum(vector<int> array,int sum) {
        vector<int> res;
        int i = 0 ;
        int j = array.size() - 1;
        while(j > i){//交叉则没有找到
            if(array[i] + array[j] == sum){
                //cout << array[i] << " " << array[j] << endl;
                res.push_back(array[i]);
                res.push_back(array[j]);
                break;
            }
            if(array[i] + array[j] > sum)
                j--;
            else
                i++;
        }
        return res;
    }
};

不用加减乘除做加法

题目描述
写一个函数，求两个整数之和，要求在函数体内不得使用+、-、*、/四则运算符号。

class Solution {
public:
    /*
    通过异或和与循环解决
    1、两个数字异或,加了非进位
    2、两个数据与，非0则左移移位，若此值不为0，则继续重复1和2直到为0.

    5-101  17-10001
    101^10001 = 10100
    101&10001 = 10 
    10100+10 = 10110 = 22(这里应该重复1和2步)
    */
    int Add(int num1, int num2)
    {
        int sum = 0 , temp  = 0;
        do{
            sum = num1 ^ num2;//1、加非进位
            temp = (num1 & num2) << 1;//2、有进位

            num1 = sum;//开始重复1和2 加非进位和进位的。
            num2 = temp;
        }while(num2 != 0);
        return num1;
    }
};

将字符串转换为整数

题目描述
将一个字符串转换成一个整数(实现Integer.valueOf(string)的功能，但是string不符合数字要求时返回0)，要求不能使用字符串转换整数的库函数。 数值为0或者字符串不是一个合法的数值则返回0。

class Solution {
public:
   /*
   策略则是遍历一遍字符串即可。
    1、地址有效NULL或空字符串
    2、数据是否上下溢出
    3、有无正负号
    4、错误标志输出
   */
    enum Status{kValid = 0 , kInvalid};
    int g_nStatus = kValid;//全局标志 
    int StrToInt(string str) {
        g_nStatus = kInvalid;
        long long num = 0;//long long 8字节，但是int 4字节，所以千万不能越界，占用4字节 最大为7f-ff-ff-ff 最小为 80-00-00-00
        const char* cstr = str.c_str();//将str转换成c字符串形式，也就是指针指向内存区域。
        if( (cstr != NULL) && (*cstr != '\0') )//1、防御性编程 字符存在且第一个非空，则继续处理
        {
            int minus = 1;//标记字符串符号
            if(*cstr == '-')//第一个为减号
            {
                minus = -1;
                cstr++;//指向下一个字符
            }
            else if(*cstr == '+')//第一个为加号
                cstr++;

            while(*cstr != '\0')//循环处理全部字符
            {
                if(*cstr > '0' && *cstr < '9')//为数字
                {
                    g_nStatus = kValid;//因为是数字，则有效。
                    //2345 =  ( ( (0*10+2) * 10 + 3)*10+4 )*10 + 5 这就是霍顿算法。
                    //这种迭代很聪明
                    num = num * 10 + (*cstr -'0');//字符串转换数字迭代计算
                    cstr++;//指向下一个
                    if( ( (minus > 0) && (num > 0x7FFFFFFF) ) ||
                        ( (minus < 0) && (num < (int)0x80000000) ) )//是否越界？
                    {
                        g_nStatus = kInvalid;//无效，返回0
                        return 0;//无效，则直接返回0
                    }
                }
                else
                {
                    g_nStatus = kInvalid;//中间含有非数字字符串，则标记此无效
                    return 0;
                }
            }
            return (num*minus);
        }
        g_nStatus = kInvalid;//无效，则直接返回0,并且标记无效。
        return 0;
    }
};

数组中重复的数字

题目描述
在一个长度为n的数组里的所有数字都在0到n-1的范围内。 数组中某些数字是重复的，但不知道有几个数字是重复的。也不知道每个数字重复几次。请找出数组中任意一个重复的数字。 例如，如果输入长度为7的数组{2,3,1,0,2,5,3}，那么对应的输出是第一个重复的数字2。

class Solution {
public:

    #define BITWORD 32
    //一个int占用4字节，对应32位
    #define SHIFT 5
    //判断数据在哪个数组中的哪一位，通常的做法就是  num/32 = n余m,n代表第几个数组，m代表这个数组的第几位，
    //shift = 5 通过移位简化了除法。
    #define MASK 31
    通过&简化了取余操作。

    //i>>SHIFT选取第几个数组元素，(1<<(i & MASK))元素第几位置高。
    void SetBit(int *a , unsigned int i){
        a[i>>SHIFT] |= (1<<(i & MASK));
    }
    //i>>SHIFT选取第几个数组元素，(1<<(i & MASK))元素第几位置高。
    void ClrBit(int *a ,unsigned int i){
        a[i>>SHIFT] &= ~(1<<(i & MASK));
    }
    //i>>SHIFT选取第几个数组元素，(1<<(i & MASK))元素第几位置高。
    bool TestBit(int *a , unsigned int i){
        return a[i>>SHIFT] & (1<<(i & MASK));//这一位是否为1
    }
    bool duplicate(int numbers[], int length, int* duplication) {
        if(length <= 1){
            *duplication = -1;
            return false;
        }
        int maxNumber = length;
        //int a[1+maxNumber/BITWORD] = {0};//确保数组表示
        int *a = (int *)malloc(sizeof(int) *(1+maxNumber/BITWORD));
        memset(a,0,sizeof(int) *(1+maxNumber/BITWORD));
        for(int i = 0 ; i < length ; i++){
            if(!TestBit(a,numbers[i]))
                SetBit(a,numbers[i]);
            else{
                *duplication = numbers[i];
                return true;
            }
        }
        *duplication = -1;
        return false;
    }
};

矩阵中的路径

题目描述
请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则之后不能再次进入这个格子。 例如 a b c e s f c s a d e e 这样的3 X 4 矩阵中包含一条字符串”bcced”的路径，但是矩阵中不包含”abcb”路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

class Solution {
public:
    bool hasPath(char* matrix, int rows, int cols, char* str)
    {
        /*char **flag = (char **)malloc(sizeof(char *)*rows);//生成Flag标记
        for(int i = 0 ; i < rows ; i++){//内存分配并清0
            flag[i] = (char *)malloc(sizeof(char)*cols);
            memset(flag[i] , 0 , sizeof(char)*cols);
        }*/
        //这里完全可以用一维数字模拟二维数组的使用，使内存连续分配
        char *flag = (char *)malloc(sizeof(char)*rows*cols);//连续空间，仅仅需要按照二维访问即可
        memset(flag , 0 , rows*cols);
        //找到可能的每个字符开始，然后开始遍历，找到可能的一条路径即可
        for (int i = 0; i < rows; i++) {
            for (int j = 0; j < cols; j++) {
                if (helper(matrix, rows, cols, i, j, str, 0, flag))
                    return true;
            }
        }
        return false;
    }
    //matrix 二维矩阵 rows行 cols列 i j分别对应当前位置  str表示目标字符 k表示第k个目标 flag标记是否被访问过
    bool helper(char *matrix, int rows, int cols, int i, int j, char *str, int k, char *flag) {
        int index = i * cols + j;//这是模拟二维数组的关键
        if (i < 0 || i >= rows || j < 0 || j >= cols || matrix[index] != str[k] || flag[index] == 1)
            return false;
        if(k == strlen(str) - 1) 
            return true;//比到最后一个字符
        flag[index] = 1;//标记为1
        if (helper(matrix, rows, cols, i - 1, j, str, k + 1, flag)        //左
            || helper(matrix, rows, cols, i + 1, j, str, k + 1, flag) //右
            || helper(matrix, rows, cols, i, j - 1, str, k + 1, flag) //上
            || helper(matrix, rows, cols, i, j + 1, str, k + 1, flag))//下 
        {
            return true;
        }
        flag[index] = 0;//回溯起来
        return false;
    }
};

把数组排成最小的数

题目描述
输入一个正整数数组，把数组里所有数字拼接起来排成一个数，打印能拼接出的所有数字中最小的一个。例如输入数组{3，32，321}，则打印出这三个数字能排成的最小数字为321323。

class Solution {
public:
    /*  将数据按照某种方式进行排序，然后获取排序后的值
    1、比较两个拼接在一起的数字大小nm和mn，因为数字可能比较大，所以转换成字符串如果mn
    //为什么此处必须是static,定义两个数字如何比较即可
    static bool cmp(int a,int b){
        string A="";
        string B="";
        A+=to_string(a);
        A+=to_string(b);
        B+=to_string(b);
        B+=to_string(a);
        return A < B;
    }/*
    sort中的比较函数compare要声明为静态成员函数或全局函数，不能作为普通成员函数，否则会报错。 
    因为：非静态成员函数是依赖于具体对象的，而std::sort这类函数是全局的，因此无法在sort中调用非静态成员函数。
    静态成员函数或者全局函数是不依赖于具体对象的, 可以独立访问，无须创建任何对象实例就可以访问。
    同时静态成员函数不可以调用类的非静态成员，这个是C++的特性，一定要搞清楚的哦。
    */
    string PrintMinNumber(vector<int> numbers) {
        string  answer = "";
        sort(numbers.begin() , numbers.end() , cmp);
        for(int i=0 ; ireturn answer;
    }
};

数组中的逆序对

题目描述
在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数P。并将P对1000000007取模的结果输出。 即输出P%1000000007。

/*
    归并排序的应用，先打印出来，然后再后续讨论结构
    */
class Solution {
    public:
    int InversePairs(vector<int> data) {
        if(data.size() <= 1)//防御性编程 
            return 0;
        int* copy=new int[data.size()];
        memset(copy , 0 , sizeof(int)*data.size());
        //调用递归函数求解结果
        int count = MergeSort(data , copy , 0 , data.size()-1);
        delete[] copy;//删除临时数组
        return count;
    }
    int MergeSort(vector<int>& data,int *copy,int start,int end)
    {
        if(start==end)
        {
            copy[start]=data[start];
            return 0;
        }
        //将数组拆分成两部分
        int length=(end-start)/2;//这里使用的下标法，下面要用来计算逆序个数；也可以直接使用mid=（start+end）/2
        //分别计算左边部分和右边部分
        int left  = MergeSort(data,copy,start,start+length)%1000000007;
        int right = MergeSort(data,copy,start+length+1,end)%1000000007;

        //进行逆序计算
        int i = start + length;//前一个数组的最后一个下标
        int j = end;//后一个数组的下标
        int index = end;//辅助数组下标，从最后一个算起
        int count = 0;
        while(i >= start && j >= start+length+1)
        {
            if(data[i] > data[j])//都是逆序对
            {
                copy[index--]=data[i--];
                //统计长度
                count += j-start-length;
                if(count>=1000000007)//数值过大求余
                    count%=1000000007;
            }
            else//不是逆序对，但是数据得拷贝排序
            {
                copy[index--]=data[j--];
            }
        }
        //下面两个for仅仅可能会执行其中一个
        for( ; i >= start; --i)//为了排序
        {
            copy[index--]=data[i];
        }
        for(; j >= start+length+1 ; --j)//为了排序
        {
            copy[index--]=data[j];
        }
        //排序本次数组
        for(int i=start; i<=end; i++) {
            data[i] = copy[i];
        }
        //返回最终的结果
        return (count + left + right)%1000000007;
    }
};

整数中1出现的次数（巧妙的解答）

求出1~13的整数中1出现的次数,并算出100~1300的整数中1出现的次数？为此他特别数了一下1~13中包含1的数字有1、10、11、12、13因此共出现6次,但是对于后面问题他就没辙了。ACMer希望你们帮帮他,并把问题更加普遍化,可以很快的求出任意非负整数区间中1出现的次数（从1 到 n 中1出现的次数）。

class Solution {
public:
    int  NumberOf1(int n) {
        int count = 0;
        while(n != 0){
            if(n%10 == 1)
                count++;
            n = n/10;//将最左边的一位清0
        }
        return count;
     }
    int NumberOf1Between1AndN_Solution(int n)
    {
        /* 这是土方法
        int sum = 0;
        for(int i = 0 ; i <= n ; i++){
            sum += NumberOf1(i);
        }
        return sum;
        */
/*以下是高级方法分析
  主要思路：设定整数点（如1、10、100等等）作为位置点i（对应n的各位、十位、百位等等），
  分别对每个数位上有多少包含1的点进行分析。

 从一个5位的数字讲起,分以下3种情况讨论：
    1、百位数字>=2  example: 31256  当其百位为>=2时，有以下这些情况满足(为方便起见，计312为a，56为b)：
          100 ~   199
         1100 ~  1199
            .....
        31100 ~ 31199
        其余都不满足！
     因此，百位>=2的5位数字，其百位为1的情况有（a/10+1）*100个数字，（a/10+1）=>对应于 0 ~ 31，
     且每一个数字，对应范围是100个数（末尾0-99）

    2、百位数字 == 1，example: 31156 当其百位为1时，有以下这些情况满足：
           100 ~   199
          1100 ~  1199
            ......
        30100 ~ 30199
        31100 ~ 31156
        其余不满足
      因此，百位为1的5位数字，共有（a/10）*100+(b+1)

    3、百位数字 ==0 example: 31056 当其百位为0时，有以下这些情况满足：
          100 ~   199
         1100 ~  1199
        30100 ~ 30199
        其余都不满足
       因此，百位数为0的5位数字，共有(a/10)*100个数字满足要求
    为什么下面要加8呢？可以通过一个式子，将上述全部结果归为一个函数
      因为只有大于2的时候才会产生进位等价于（a/10+1），当等于0和1时就等价于(a/10)。
      另外，等于1时要单独加上(b+1)，这里我们用a对10取余是否等于1的方式判断该百位是否为1。
        */
        int count = 0;
        long long i = 1;
        for(i = 1 ; i <= n ;i *= 10)
        {
            //i表示当前分析的是哪一个数位
            int a = n / i;
            int b = n % i;
            count = count + (a+8)/10*i + (a%10 == 1) * (b+1);
        }
        return count;
    }
};