实践 - 使用Python画一棵递归分形树

本实践中，作者要介绍用Python在Tkinter上画一棵树的方法。通过本实践，读者可以：练习面向对象的程序设计方法；了解生成器的使用方法；运用递归函数；了解Tkinter画图的基本方法；以及学习“树”这种重要的数据结构。

版权声明

本文可以在互联网上自由转载，但必须：注明出处(作者：海洋饼干叔叔)并包含指向本页面的链接。

本文不可以以纸质出版为目的进行改编、摘抄。

本文节选自作者的《Python编程基础及应用》视频教程。

本实践中，作者要介绍用Python在Tkinter上画一棵树的方法。通过本实践，读者可以：练习面向对象的程序设计方法；了解生成器的使用方法；运用递归函数；了解Tkinter画图的基本方法；以及学习“树”这种重要的数据结构。

​ 在本书配套的网站上，你可以下载到本实践的全部代码。本章要画的图“大概”长成下面这样。为什么说是大概呢？ 因为树的结构是在一定约束条件下随机生成的。

1. 数据结构 - 树

​ 要完成本实践，读者首先要了解一点数据结构 - data structure的知识。数据结构大概是指计算机内部表达和组织数据的方式。

1.1 树

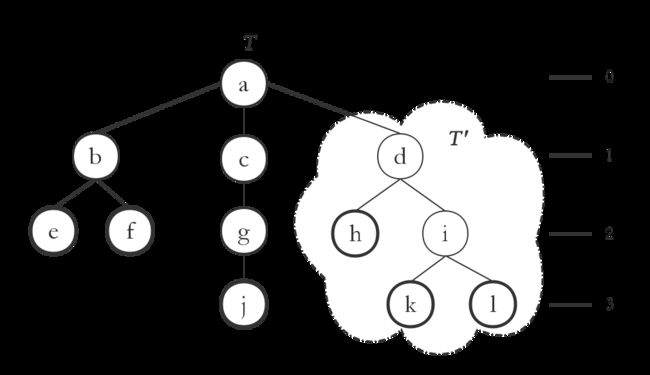
​ 树-Tree是一种数据结构，它用于模拟真实世界中的树形结构，通常描绘成上图的样子。为了说明方便，作者把每个节点用字母作了标识。

​ T是一棵树，树上的每个圆圈称之为一个节点-node，其中，a是树T的根节点 - root node。节点可以有后代 - descendents，其中，直接的后代称为儿子节点 - child。上图中，b,c,d是节点a的儿子，h,i是节点d的儿子。有儿子的节点称为内节点，没有儿子的节点称为叶子-leaf。上图中，e,f,k等节点没有儿子，作者用粗线圆作了标识，它们是叶子。

​ T’是树T的一棵子树-sub tree，其根节点为d，我们称树T’是树T中以d节点为根的子树。理论上，任何一个节点其及全部后代都可视为一棵树。

​ 上树中右侧的数字0,1,2,3表示节点在树中的深度-depth。a节点的深度为0，g,h节点的深度为1，j,k,l节点的深度为3。

1.2 树的递归表示

class TreeNode:
    def __init__(self,label):
        self.sLabel = label
        self.children = []

a = TreeNode('a')
b = TreeNode('b')
c = TreeNode('c')
d = TreeNode('d')
a.children.extend([b,c,d])
b.children.extend([TreeNode('e'),TreeNode('f')])
...

​ 上边的代码展示了一个表示树的Python递归结构。TreeNode类有一个sLabel属性，存储节点的标签。此外，该类还有一个类型为列表的数据成员children，这里面存储该结点的全部儿子节点。而儿子节点的类型也为TreeNode，其也有children列表用于存储该儿子节点的儿子。当一个TreeNode对象的children列表为空时，表明该节点为叶子。

​ 上述代码的后几行建立了前小节中树结构的一部分。其中a为根节点，a有b,c,d三个儿子，而b又有两个儿子e和f…

2. Top-Left坐标系

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6MOpO1zu-1578801407595)(/images/1542197988935.png)]

​ 在图形程序设计中，一般采用Top-Left坐标系。如上图，以屏幕或者窗口的左上角为原点，横向为x轴，纵向为y轴。位置越靠右，x越大；位置越靠下，y越大。窗口内的任意一个点，可用一对(x,y)构成，这一对(x,y)值，称为该点的坐标。

3. 实例中的树表达

class Point:
    def __init__(self, x, y):
        self.x = x
        self.y = y

class TreeNode:
    maxDepth = 8
    nBranches = 3
    def __init__(self, bottom, top, depth=0):
        self.bottom = bottom
        self.top = top
        self.drawingTop = top
        self.depth = depth
        self.children = []
        self.__generateDescendents()

​ 如代码所示，Point类有成员x和y，表明一个坐标点。TreeNode类表示一个树节点。类成员maxDepth表示树所允许的最大深度。类成员nBranches表示“建议”的树分叉数，即一根树支将分出多少根下层树支。此处之所以用了“建议”一词，是因为实际树的生成过程中分支数会引入随机成分。

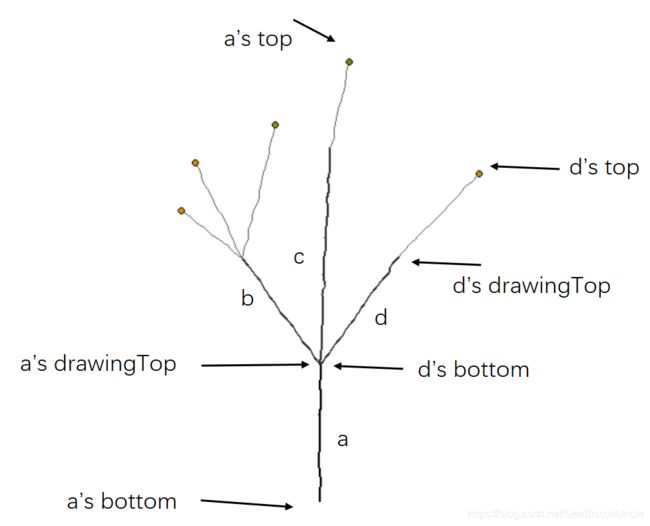
​ TreeNode对象的children属性是其儿子列表，depth表示该节点在树中的深度。TreeNode对象的另外几个属性需要结合下图来理解，这是作者在树上取下的一个小树支。下图中，a是一个TreeNode节点，其bottom表示以该节点为根的子树的“下”顶点；其top表示以该节点为根的子树的“上”顶点。注意，这里的上下打了引号，那是因为实践中，树支因地球引力，可能事实上倒垂向下。

​ drawingTop定义为该节点自身（不含其子孙）的描绘用“上”顶点。a节点在树中的实际表现为一段树支，树支的描绘范围即为bottom至drawingTop点。从drawingTop一直到top则是a的子孙们的描绘区域。下图中，b,c,d为a的儿子，b,c,d也是TreeNode类型，其bottom应等于a的drawingTop。

​ 此外，TreeNode类构造函数的最后一行执行了一个“不公开”成员函数__generateDescendents()，这个函数将递归生成以该节点的根的子树，该子树中节点的深度不超过TreeNode.maxDepth。该部分内容见后节。

变量、函数、类的判定准则
- 新手们写出来的程序通常可读性和健壮性都有问题。作者建议，当读者试图定义一个变量、函数、类时，都必须满足如下规则：如果其作用和取值可以用简洁明了没有歧义的讲清楚，那么其存在可能是合理的。如果说不清道不明，那么读者需要另寻它法。本实践中的，TreeNode之bottom,top,drawingTop，受限于其复杂性，很难用一句话描述，但至少借助于图示，是可以讲清楚的。 - Python之禅里有“If the implementation is easy to explain, it may be a good idea"。这里，请读者品味其含义。

4. 树的递归生成

4.1 分叉树支生成

class TreeNode:
    ...
    def __generateDescendents(self):
        "Recursively build sub-tree of the current node."
        n = random.randint(TreeNode.nBranches//2,round(TreeNode.nBranches*1.5))
        n = n if n >=1 else 1

        r = 0.20 + random.random() * 0.2
        x = self.bottom.x + (self.top.x - self.bottom.x) * r
        y = self.bottom.y + (self.top.y - self.bottom.y) * r
        self.drawingTop = Point(x, y)

        if self.depth < self.maxDepth:
            a = math.pi * 0.5 / n
            for i in range(n):
                angleOffset =  a * (n-1) / 2 - a * i + math.pi
                angleOffset *= (0.9 + random.random() * 0.2)
                son = self.__bornSon(self.drawingTop, self.top, angleOffset)
                self.children.append(son)

​ 上述__generateDescendents()函数在节点的构造函数中被调用。从下到下解释该函数。

​ 首先，函数确定当前树支的分叉数，也就是当前节点的儿子的数量n。可以看到，n随机取值为TreeNode.nBranches的0.5到1.5倍。为了稳妥起见，程序还限定n值至少为1。

​ 接下来，程序确定当前树支的描绘顶点，即当前节点的drawingTop。drawingTop的确定也引入了随机性，从bottom顶点出发，往top顶点方向，前进总距离的0.2 - 0.4倍，即确定为drawingTop顶点。这里，random.random()返回[0,1)之间的随机浮点数，1之后的)号表明返回值不包含1，这说明，r的取值为0.2 - 0.4(不含)。

​ 然后，如果当前节点的深度-depth小于约定的最大深度-maxDepth，则生成该节点的n个儿子结点，也就是当前树支的n个分叉。这里的代码比较复杂，涉及了弧度和三角函数的数学知识，简要描述之。如前节所述，当前节点/树支的drawingTop即为儿子节点/分叉的bottom。在当前节点/树支的drawingTop点，沿当前树支的伸展方向，左右各45度，共90度(即 π/2)范围内逐一"均布"生成n个分叉儿子节点。这里的“均布”是大致的，上述代码中的angleOffset被乘以了0.9-1.1的随机数。__bornSon(self.drawingTop, self.top, angleOffset)函数以当前树支的drawingTop为bottom，以“以当前树支为根的子树”的top为top，生成一个分叉儿子结点，分叉的伸展角度为当前树支的伸展角度加上偏移角angleOffset。 一个儿子生成完后，再将其加入到children列表中。

4.2 生成一个儿子

 class TreeNode:
        ...
    def __bornSon(self, bottom, top, angleOffset):
        "Born a son of current node, with designated offset angle."
        xWidth = top.x - bottom.x    #Width of sub-tree
        yHeight = top.y - bottom.y   #Height of sub-tree
        angleSubTree = math.atan(yHeight / xWidth) if xWidth !=0 else math.pi/2
        if (angleSubTree < 0 and bottom.y > top.y) or \
                (angleSubTree > 0 and bottom.y < top.y):
            angleSubTree += math.pi
        angleSon = angleSubTree + angleOffset

        r = 0.9 + random.random() * 0.2
        c = math.sqrt(xWidth ** 2 + yHeight ** 2) * r
        xOffset = c * math.cos(angleSon)
        yOffset = c * math.sin(angleSon)
        topNew = Point(xOffset + bottom.x, yOffset + bottom.y)
        return TreeNode(bottom, topNew, self.depth + 1)

​ 接上节，该函数需要沿其子树的伸展方向偏转一个偏移角生成一个儿子。

​ 函数首先通过bottom，top之间的相对位置关系，使用反正切函数计算得到子树的伸展角angleSubTree。请注意，由于反正切函数的局限性(值域为(-π/2, +π/2)，不能表达全部圆周角度），代码不得不再次通过bottom, top的相对关系对angleSubTree进行修正。接下来，子节点的伸展角angleSon等于子树伸展角加上偏移角。

​ 有了分支子节点的伸展角angleSon，再借助子树的对角线长度c乘以0.9-1.1随机数，使用正余弦函数计算出分支子节点的top - topNew。然后，函数以topNew为“上”顶点构造一个TreeNode对象，子节点的深度为当前节点深度加1。

​ 需要特别说明的是，__bornSon()函数通过TreeNode构造函数生成一个子结点，而该子结点的构造函数又会执行__generateDescendents()函数生成其后代。所以，只要我们通过TreeNode的构造函数构造一个根节点-root node，该节点的构造函数会执行__generateDescendents()生成其子结点，而子结点的构造又会导致子结点的子结点被生成出来，… ，最终，生成了一棵完整的树。在生成后代的过程中，只有当当前节点的深度小于约定的最大深度时，才会尝试生成后代，因此，递归有恰当的边界条件会导致其终结。这种情况，我们也称递归函数会收敛。

4.3 生成整棵树

class TreeBuilder:
    def setPara(bottom,top,nBranches=3,maxDepth=8):
        TreeBuilder.bottom = bottom
        TreeBuilder.top = top
        TreeBuilder.nBranches = nBranches
        TreeBuilder.maxDepth = maxDepth

    def buildTree(depthOffset=0):
        TreeBuilder.maxDepth += depthOffset
        TreeBuilder.maxDepth = TreeBuilder.maxDepth \
            if TreeBuilder.maxDepth <=10 else 10
        TreeBuilder.maxDepth = TreeBuilder.maxDepth \
            if TreeBuilder.maxDepth >=2 else 2

        print("Build a tree, branches:{},depth:{}.".
              format(TreeBuilder.nBranches,TreeBuilder.maxDepth))
        TreeNode.maxDepth = TreeBuilder.maxDepth
        TreeNode.nBranches = TreeBuilder.nBranches
        t = TreeNode(TreeBuilder.bottom,TreeBuilder.top)
        RenderHelper.showTree(t)
 ... 

 TreeBuilder.setPara(bottom=Point(1024/2,768-20),
                        top=Point(1024/2,768*0.1))
 TreeBuilder.buildTree()

​ TreeBuilder是一个所谓的“帮助”类，可以看到其两个函数都没有self参数，都属于类函数的范畴。也就是说，这两个函数的执行不以TreeBuilder类型对象的存在为前提。

​ 在主程序中，我们首先通过TreeBuilder.setPara()函数设置了将要生成的树的bottom“下”顶点及top“上”顶点，1024和768是窗口的宽度和高度，可以看出，bottom左右居中，距窗口下边缘20个像素；top左右居中，距窗口上边缘10%。建议的树支分叉数nBranches以及树的最大深度maxDepth使用了默认值。

​ 接下来，主程序调用TreeBuilder.buildTree()函数构造并显示一棵树。这个函数允许通过一个深度偏移量来改变原设定最大深度。在调整完深度并把深度及建议分叉数存入TreeNode.maxDepth和TreeNode.nBranches后，函数简单粗暴地构造了一个TreeNode对象t，这个t即为树的根节点。请注意，由于前小节所述的递归的原因，这个以t为根的树会被完整地生成出来，其深度为TreeNode.maxDepth。

​ 请读者注意，作者对TreeBuilder.maxDepth进行了限定，不允许其超过10。原因很简单，树的节点的总数量随深度呈指数级增长，超过10的深度的树可能需要非常长的运行时间，甚至可能会超过你的计算机的存储或计算能力。

​ 在buildTree()函数的最后，执行了RenderHelper.showTree(t)将树显示出来。

5 树的显示

5.1 计算机里的颜色表示

​ 画家可以仅凭“红”，“绿”，“蓝”调出他所需要的所有颜色，计算机也可以。计算机通常用三个字节来表示一种颜色，从左往右分别表示红、绿、蓝三种颜色成分，取值为0-255，即十六进制的0x00 - 0xff。通过三种颜色成分的不同组合，我们可以得到任意颜色。这种用红-Red，绿-Green，蓝-Blue来组合构成颜色的模型称为RGB模型。

RGB	说明
009000	红为0x00，绿为0x90，蓝为0x00，综合颜色为翠绿
ff0000	红为0ff，绿为0x00，蓝为0x00，综合颜色为红
909000	红为0x90，绿为0x90，蓝为0x00，综合颜色为黄
ffffff	三种颜色均为0xff，综合颜色为白
000000	三种颜色均为0x00，综合颜色为黑
606060	三种颜色均为0x60，综 合颜色介于黑和白之间，是灰色，值越大，灰越浅

​ 在印刷业，使用的配色方案跟计算机里有所不同，他们使用青-Cyan、品红-Magenta和黄-Yellow来组合构成所有颜色，即所谓减色法，又称CMY模型。

5.2 树的遍历

class TreeNode:
   	...
    def bfs(self):  #breadth first search
        nodesQueue = [self]
        while True:
            if len(nodesQueue)==0:
                break
            x = nodesQueue.pop(0)
            yield x
            nodesQueue.extend(x.children)

​ 显示一棵树，即是迭代列举树的全部节点，并将其全部画出来。列举树的全部节点，又称为树的遍历。作者在这里使用了树的宽/广度优先遍历算法。

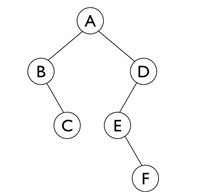
​ 为了便于读者理解，作者以上面这棵小树为例，说明宽度优先遍历的过程。对A节点执行bfs()函数，队列nodesQueue初始化为[A]。遍历过程将一直持续到nodesQueue队列为空，即len(nodesQueue)==0为止。

​ 首先，从队列中弹出A并yield。请注意，这里的bfs()函数被写成了生成器函数，关于生成器函数的工作原理，请参考本书相关章节。这里简单地认为yield x语句将x结点“抛”给使用方即可。

​ A被yeild后，A的儿子结点被加入nodesQueue - [B,D]。接下来，弹出并yield B，B的儿子结点C被加入nodesQueue - [D,C]。接着，弹出并yield D，D的儿子结点E被加入nodesQueue - [C,E]。接下来，弹出并yield C，C没有儿子，故nodesQueue只剩下一个节点 - [E]。接着，E被弹出并yield，E的儿子F被加入nodesQueue - [F]。最后，F被弹出并yield，F是叶子，没有儿子可以加入nodesQueue，所以nodesQueue为空，全部节点已经成功列举，遍历结束。

​ 如果列出全部节点的列举顺序，应该是A,B,D,C,E,F,正好是树的结点一层一层的逐层列举。这种列举了某个节点后，立即列举离这个节点最近的全部儿子的遍历方法称为“宽度优先”。与“宽度优先”对应的是“深度优先”，相关内容在数据结构课程中会得到深入研究。

5.2 树的显示

class RenderHelper:
    canvas = None
    def showTree(tree):
        "Render a tree on canvas."
        assert RenderHelper.canvas != None, "Please set canvas first."
        RenderHelper.tree = tree
        for x in RenderHelper.canvas.find_all():
            RenderHelper.canvas.delete(x)
        for x in tree.bfs():
            RenderHelper.__renderNode(x)
        RenderHelper.canvas.update()

​ 同样地，RenderHelper是一个帮助类，可以在不经实例化的情况下使用其类函数。canvas是主程序设置进来的Tkinter"画布"。showTree(tree)函数负责在canvas上把树“画”出来。

​ 可以看到，showTree()首先并断言了canvas的可用性。然后，删除了canvas内已有的全部内容。接下后，通过for x in tree.bfs()遍历列举tree的全部节点x，逐一调用__renderNode(x)在画布上“画”出来。

​ __renderNode(x)所谓的“画”其实只是在canvas的内部数据表达中增加相关元素（比如线、椭圆或其它图形），真正要把画布的内容展示在计算机屏幕上，还需要执行canvas.update()函数。

class RenderHelper:
    ...
    def __renderNode(node):
        "Render a TreeNode."
        colorFill = "#{0:0>2x}{0:0>2x}{0:0>2x}".\
            format(int(0x60 * node.depth / node.maxDepth))
        RenderHelper.__drawLine(node.bottom,node.drawingTop,
            colorFill=colorFill,width=1.5 ** (node.maxDepth - node.depth))

        if not node.children: #draw leaf if it is a leaf
            red = 0xff * node.drawingTop.y / RenderHelper.tree.drawingTop.y
            red = int(red * (0.8 + random.random() * 0.4))
            red = red if red <= 0xff else 0xff
            colorFill = "#{0:0>2x}9000".format(red)
            RenderHelper.canvas.create_oval(
                node.drawingTop.x - 3,node.drawingTop.y - 3,
                node.drawingTop.x + 3,node.drawingTop.y + 3,
                fill=colorFill)
        RenderHelper.canvas.update()     #This sentence for contruction show

​ __renderNode(node)函数负责在画布中“画”一个节点。首先，是画这个节点所代表的树支。

colorFill = "#{0:0>2x}{0:0>2x}{0:0>2x}".\
            format(int(0x60 * node.depth / node.maxDepth))

​ colorFill为形如"#101010"的RGB模型颜色字符串，在这里，R，G，B三个值相等，且跟当前节节的深度有关，深度越浅，说明节点离树根越近，colorFill为取值接近"#000000"，黑色越深。当深度较大时，说明节点离叶子较近，colorFill取值接近"#606060"，黑色较浅，为灰色。

​ __drawLine()函数从节点的bottom至drawingTop画一条线表示树支，颜色即上述colorFill，而线宽则同样与节点深度有关。深度越浅，树支越接近树根，线宽越宽。

​ 当节点的儿子列表为空时，说明节点是叶子节点，此时需要画一个实心圆点表示树叶。树叶本来是绿色(取值0x90)的，但作者刚才正好从美丽的重庆大学虎溪校区泛黄的银杏树下走过，决定给树叶加点“红”色。红色成分的多少取决于树叶的描绘高度，越靠近树顶，红色越少，树叶越绿；越靠近地面，红色越多，树叶越黄。上述的colorFill字符串格式化的结果为"#309000"这样的字符串，绿为0x90，红为0x30或者其它值，蓝始终为0x00。注意，红色成分的多少也加入了一些随机因素。

​ canvas.create_oval()函数在画布上创建一个实心圆树叶，该实心圆以drawingTop为圆心，colorFill为填充色。这个函数本来是画椭圆的，但由于正圆是椭圆的特例，所以也可以用来画正圆。

​ __renderNode()函数的最后一行为RenderHelper.canvas.update()。update()会在显示器上实际渲染画布的内容，所以该函数执行至少要"花费"一个显示帧的时间。考虑到显示器的刷新频率一般是60Hz，这意味道着，程序每秒钟只能“画”出大约60个节点。所以，如果该行代码存在，你可以在计算机上看到树被一点点的画出来，并且还可以根据树支、叶片在界面上出现的先后顺序来理解树的“深度优先遍历”算法。读者可以删除该行代码，再运行试一试。

class RenderHelper:
    ...
	def __drawLine(pt0, pt1, width, colorFill, minDist=10):
        dots = RenderHelper.__generateDotsSequence(pt0,pt1,minDist)
        RenderHelper.canvas.create_line(dots,fill=colorFill,width=width,
            smooth=True)

    def __generateDotsSequence(pt0,pt1,minDist):
        dots = []
        dx, dy = pt1.x - pt0.x, pt1.y - pt0.y
        c = math.sqrt(dx ** 2 + dy ** 2)
        n = int(c / minDist) + 1

        xPrev,yPrev = pt0.x,pt0.y
        for i in range(n):
            xOffset = dx * i / n
            yOffset = dy * i / n
            if i > 0:
                xOffset += minDist * (0.5 - random.random()) * 0.25
                yOffset += minDist * (0.5 - random.random()) * 0.25
            x,y = pt0.x + xOffset,pt0.y + yOffset
            dots.extend([xPrev,yPrev,x,y])
            xPrev,yPrev = x,y
        dots.extend([xPrev,yPrev,pt1.x,pt1.y])
        return dots

​ __drawLine()函数负责从pt0 - bottom到pt1 - drawingTop画一条宽度为width，颜色为colorFill的实心线来表示一条树支。

​ 但现实中的树，树支不可以是完全直的。所以，借助__generateDotsSequence()函数，作者以minDist=10为间距，将树支分成多个小段，并加入一些随机因素。最后，再用canvas.create_line()将多点线画出来，尽可能模仿现实世界中树支的模样。

6 Tkinter循环

    tk = tkinter.Tk()
    tk.title("Build Tree")
    canvas = tkinter.Canvas(tk,width=1024,height=768,bg="#ffffff")
    canvas.pack()

    RenderHelper.canvas = canvas
    TreeBuilder.setPara(bottom=Point(1024/2,768-20),
                        top=Point(1024/2,768*0.1))
    TreeBuilder.buildTree()

    tk.bind("n", lambda evt: TreeBuilder.buildTree())
    tk.bind("=", lambda evt: TreeBuilder.buildTree(depthOffset=1))
    tk.bind("+", lambda evt: TreeBuilder.buildTree(depthOffset=1))
    tk.bind("-", lambda evt: TreeBuilder.buildTree(depthOffset=-1))
    tk.mainloop()

​ 主程序中，我们创建了一个tkinter对象，并生成了长1024，宽768，背景色为白色的画布 - canvas。然后，建造并显示了一棵树。

​ 接下来，我们对程序创建了几个快捷键，程序运行中，当你按下n时，TreeBuilder.buildTree()会被执行，这将建造并显示一棵新树。按下+或者=时，TreeBuilder.buildTree(depthOffset=1)会被执行，系统会尝试将树的深度加1并建造和显示一棵新树。按下-时，TreeBuilder.buildTree(depthOffset=-1)，系统会尝试将树的深度减1并建并建造和显示一棵新树。

​ 此处的lambda表示匿名函数，它将带有实参的TreeBuilder.buildTree(depthOffset=1)封装成一个没有名字的函数。

​ tk.mainloop()将执行所谓的消息循环，在里面，Tkinter将不断地循环等待来自用户的命令并执行，直到用户关闭Tkinter窗口。

7 小结

​ 本实践的主要用意在于帮助读者掌握和运用面向对象的程序设计方法，以及递归的算法、树的数据结构表示方法等。Tkinter库的使用不是重点。作为Python自带的标准GUI工具包，Tkinter库在小型应用中仍有一席之地，但当应用的规模略大时，作者认为不太方便。在本书中，作者将着重介绍另一种更强大的GUI工具包，那就是PyQt。

本文节选自作者的《Python编程基础及应用》视频教程。想完整零基础学习Python程序设计，欢迎使用此免费视频教程。