第一次作业
设计思路:
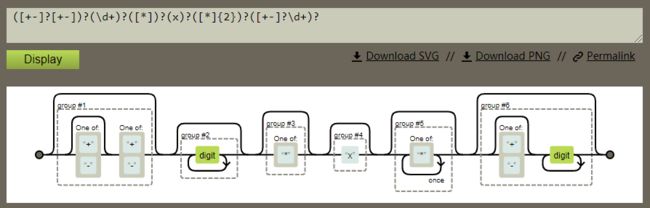
第一次作业的主要要求为实现多项式的读入,通过正则表达式拆分成各个power型项,最后进行求导输出。由于要求的功能较为简单,我只设计了两个类,分别是Word类来储存每一项的系数与指数,Main函数类进行解析,求导,和输出最终的结果。整个工程主要的难点在于读入整行字符串时如何将其分成带符号的各个项,下面是用于解析的正则表达式的效果。
正则解析:
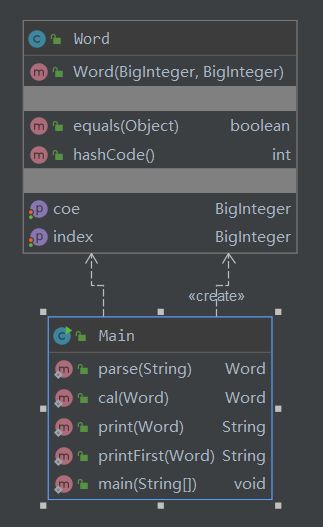
UML类图:
基于度量的程序结构分析:
通过IDEA下的Metrics Reloaded 插件进行复杂度分析和依赖度分析。
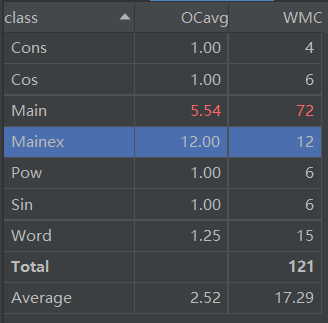
度量分析图如下:
分析发现Main函数下的parse方法和其所调用的其他方法的联系十分紧密,即耦合度较高且循环复杂度较高,这也是第一次作业中我 “ 1main到底 ” 的面向过程设计思路的弊端,也没能较好的拆分方法,没能较好的实现高内聚、低耦合的项目设计目标。
Bug分析:
我方 :
这次作业我在强测中没有出bug,而在互测中经同学的Hack,发现了例如“-- x”等输入,如果x与其前面的双重符号中间存在空格,我将只能识别到第一个符号的bug。出bug的原因在于我没能仔细的阅读指导书,没能提前想到“-- x”的情况存在,修复时对字符串提前进行空格处理即可。
对方 :
互测时主要使用评测机对对方代码进行测试,通过Python的xeger和sympy 库进行随机的多项式格式生成与计算比较。主要重点部分如下:
def random_poly(): xe = Xeger(limit=20) regex = r"[\t ]*([+\-][\t ]*)((((([+\-]?[1-9]+)[\t ]*[*][\t ]*)|([+\-]))" \ r"?(x([\t ]*([*]{2}[\t ]*([+\-]?[1-9]+)))?))|([+\-]?[1-9]+))[\t ]*" ran_poly = str() for j in range(50): ran_poly += xe.xeger(regex) return ran_poly
在测试中,发现两位同学分别有:没能正确使用BigInterger处理大数,没能正确解析字符串中间出现的 “ -+ ” “ +- ” 等连续符号的问题。
第二次作业
设计思路:
第二次作业相较第一次作业主要添加了sin(x),cos(x)的输入情况,以及在较为简单的情况下判断并输出WF,相比于第一次作业在设计上则主要新增了sin,cos,pow,cons类,且四者分别继承自Word,即项类。整体作业难度也在于正则表达式的解析,WF的判断依据则根据两次匹配对应项的字符串中间是否存在非空格的字符来完成,这也是我认为比较新颖的地方。
正则解析:
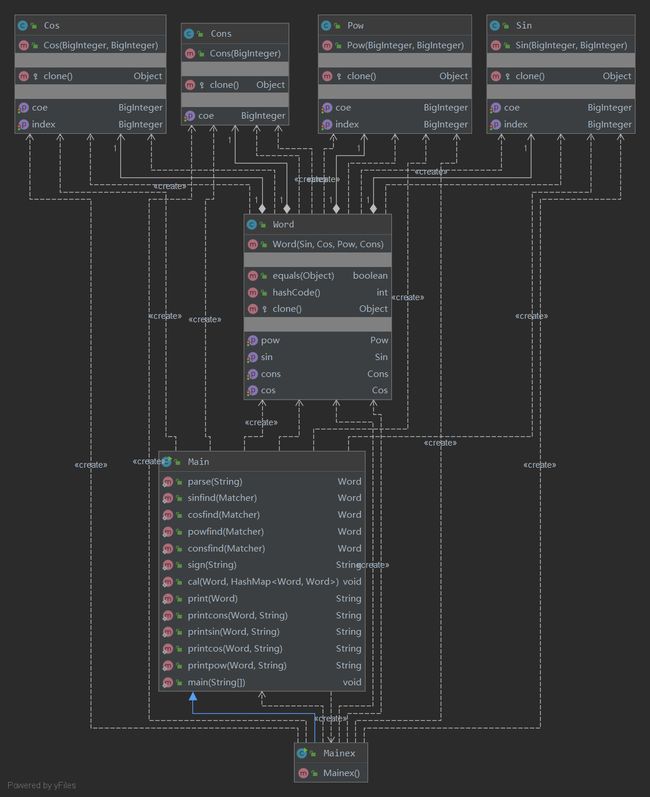
UML类图:
基于度量的程序结构分析:
通过IDEA下的Metrics Reloaded 插件进行复杂度分析和依赖度分析。
度量分析图如下:
分析发现Main Class和Mainex Class 的复杂度的仍然很高,虽然实现了继承结构模式,但没有合理的处理拆分方法与方法的位置,导致问题发生,这些部分将在我的第三次作业中实现较为完善的优化。
Bug分析:
我方 :
这次作业在强测与互测中没有Bug发现。
对方 :
互测思路与第一次类似,通过构造随机数评测机进行测试,主要部分如下
def random_poly(): xe = Xeger(limit=20) regex =r'[ \t]{0,3}([*][ \t]{0,3}|[+\-][ \t]{0,3}[+\-]?[ \t]{0,3})' \ r'(((cos[ \t]{0,3}\([ \t]{0,3}x[ \t]{0,3}\)' \ r'|sin[ \t]{0,3}\([ \t]{0,3}x[ \t]{0,3}\)|x)' \ r'([ \t]{0,3}(\*\*[ \t]{0,3}([+\-]?\d{1,2})))?)' \ r'|([+\-]?\d{1}))[ \t]{0,3}' ran_poly = str() for j in range(50): ran_poly += xe.xeger(regex) return ran_poly
在测试中,发现一位同学存在例如“ ++8*7* cos ( x ) ”等多个常数项相乘时,会自动忽略第一项的问题
第三次作业
设计思路:
第三次作业较前两次作业有了难度上的极大提升,其中主要包括非规则的括号嵌套结构,正则匹配的贪婪算法导致对于例如“cos(x)*(x)“等类型的表达式不可直接解析,需要一定的预处理。
在设计上,解析算法层面,我选择先对括号进行解析,从识别最内层" ( "," ) ",将其中的内容保存到Hashmap中,再将该层的括号替换成" [ "," ] " (当然前提是在一开始读入字符串时已经扫描过字符串,鉴别有无非法字符" [ "," ] " )。这样处理就较好的解决递归终点判断与正则解析时由于贪婪导致的捕获组不满足要求的问题。
UML类图:
基于度量的程序结构分析:
通过IDEA下的Metrics Reloaded 插件进行复杂度分析和依赖度分析。
度量分析图如下:
| method |
ev(G) | iv(G) | v(G) |
| Cons.Cons(BigInteger,BigInteger,Term) | 1.0 | 1.0 | 1.0 |
| Cons.printTerm() | 1.0 | 1.0 | 1.0 |
| Cos.calcDer() | 1.0 | 4.0 | 4.0 |
| Cos.clone() | 1.0 | 1.0 | 1.0 |
| Cos.Cos(BigInteger,BigInteger,Term) | 1.0 | 1.0 | 1.0 |
| Cos.printTerm() | 1.0 | 4.0 | 4.0 |
| Main.getLists() | 1.0 | 1.0 | 1.0 |
| Main.main(String[]) | 1.0 | 9.0 | 10.0 |
| Main.setLists(ArrayList |
1.0 | 1.0 | 1.0 |
| Nest.calcDer() | 1.0 | 2.0 | 2.0 |
| Nest.clone() | 1.0 | 1.0 | 1.0 |
| Nest.getNest() | 1.0 | 1.0 | 1.0 |
| Nest.Nest(HashMap |
1.0 | 1.0 | 1.0 |
| Nest.printTerm() | 1.0 | 5.0 | 5.0 |
| Nest.setNest(HashMap |
1.0 | 1.0 | 1.0 |
| Pow.calcDer() | 1.0 | 3.0 | 3.0 |
| Pow.clone() | 1.0 | 1.0 | 1.0 |
| Pow.Pow(BigInteger,BigInteger,Term) | 1.0 | 1.0 | 1.0 |
| Pow.printTerm() | 1.0 | 2.0 | 2.0 |
| Sin.calcDer() | 1.0 | 4.0 | 4.0 |
| Sin.clone() | 1.0 | 1.0 | 1.0 |
| Sin.printTerm() | 1.0 | 4.0 | 4.0 |
| Sin.Sin(BigInteger,BigInteger,Term) | 1.0 | 1.0 | 1.0 |
| Term.getCoe() | 1.0 | 1.0 | 1.0 |
| Term.getIndex() | 1.0 | 1.0 | 1.0 |
| Term.getInner() | 1.0 | 1.0 | 1.0 |
| Term.setCoe(BigInteger) | 1.0 | 1.0 | 1.0 |
| Term.setIndex(BigInteger) | 1.0 | 1.0 | 1.0 |
| Term.setInner(Term) | 1.0 | 1.0 | 1.0 |
| Term.Term(BigInteger,BigInteger,Term) | 1.0 | 1.0 | 1.0 |
| Word.addNewTerm(Term) | 1.0 | 2.0 | 2.0 |
| Word.doDerivative() | 1.0 | 2.0 | 2.0 |
| Word.getMap() | 1.0 | 1.0 | 1.0 |
| Word.mapSize() | 1.0 | 1.0 | 1.0 |
| Word.printWord() | 1.0 | 5.0 | 5.0 |
| WordMaker.consFind(Matcher) | 1.0 | 6.0 | 6.0 |
| WordMaker.cosFind(Matcher) | 1.0 | 7.0 | 7.0 |
| WordMaker.nestFind(Matcher) | 1.0 | 2.0 | 2.0 |
| WordMaker.parse(ArrayList) | 1.0 | 7.0 | 7.0 |
| WordMaker.powFind(Matcher) | 1.0 | 6.0 | 6.0 |
| WordMaker.sign(String) | 2.0 | 2.0 | 4.0 |
| WordMaker.sinFind(Matcher) | 1.0 | 10.0 | 10.0 |
| WordMakerEx.getMap() | 1.0 | 1.0 | 1.0 |
| WordMakerEx.judgeValid(StringBuilder) | 1.0 | 2.0 | 2.0 |
| WordMakerEx.setMap(HashMap |
1.0 | 1.0 | 1.0 |
| WordMakerEx.WordMakerEx(StringBuilder) | 3.0 | 6.0 | 7.0 |
| Total | 51.0 | 121.0 | 125.0 |
| Average | 1.0625 | 2.5208333333333335 | 2.6041666666666665 |
通过与前两次作业项目复杂度的对比发现,通过将求导计算,字符串parse识别等方法分别下放到Sin Cos等Class中,极大简化了Main Class的复杂度,相较之前的一main到底有了较大的提升。并且在求导运算过程中,因子的符号与定位已经确定,不需要考虑因子间的关系,在运用链式求导法则时,因子间能相互完全独立,达到解耦合的目的。
Bug分析:
我方 :
这次作业在强测与互测中发现的bug在于我处理例如 “ -- x “,” +- 1 “ 等应当被当做表达式的字符串时,由于没有正确的解析中间的空格,程序会将其解析成正常的因子,最终导致例如 ” sin(-- 1)“等错误的输入无法输出 ” Wrong Format!“
另外一个bug原因在于最初没有对针对pow类型进行嵌套处理,导致处理括号外面的符号时无法正确识别,例如sin((x-(x)))无法成功计算,修改时将原先没有增加系数(默认为1)的nest类增加系数即可。
对方 :
由于这次没能很好的写出覆盖完善的评测机,在hack部分便主要采用覆盖性测试的方法,针对该次作业的特殊情况,我的测试数据主要集中在一下方面:
(1)爆破tle和正则 : "((((((((((x))))))))))”
" ((((((((((((((x)*x)*x)*x)*x)*x)*x)*x)*x)*x)*x)*x)*x)*x) ”
" -x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x)))))))))))))) ”
(2)针对化简坑点的测试 : “ cos((x*x)) “ “ sin(x)*(x) ” “ sin((++(-+(x)))) ”
(3)边缘数据测试 : “ -(x)**50 “
创建模式:
设计的思路在前文每次作业的分析中已经提及,下面主要讲讲我自己在创建模式设计时的一点心得。
由于前两次作业整体结构较为简单,在一开始书写代码的时候,我没有太注重提前的结构设计架构,可以说是完全按照面向过程的程序设计,结果化体系也只体现在对于多项式的项这一个大类上面使用了工厂化思想,还是没有摆脱一main到底的糟糕布局。在第三次作业中,由于本身多项式的解析复杂度大幅度上升,我曾尝试使用第二次的创建模式作为模板,结果在给sin,cos类添加cal方法进行求导时,发现判断到递归终点时要引用多个Main里的方法,即两个类的V(G)指数较高,关联度强,导致耦合度极高,且继承关系十分混乱,最后只能含泪重构,保留了之前的sin cos cons pow类,新增wordmaker等专门对解析出来的项进行运算,再用term,nest类构造数据的保存格式,从而达到解耦合的效果。
对比和心得
对比:
通过和老师助教们整理出来的优秀代码作业进行对比,我发现很多优秀的代码都是通过表达式树的形式实现的,尤其是看了tyh大佬用一个 Lexer 转成 token 表示,然后用 Shunting yard进行表达式解析的方法,真的学到了很多,比其我之前的超长正则捕获来讲,无论是可维护性还是可阅读性都强了太多。还有lyj大佬写的自动机与栈处理,也十分清晰得当,相较我的直接一股脑丢进map里要简约美观很多
心得:
第一个单元的作业总体感觉前两次难度较低,到第三次难度有了较大的提高,由于前两次我并没很好的进行结构设计与整体的包装设计,导致第三次要求过程复杂后进行了大量的重构,这是我不太满意的地方,希望在第二单元的学习中我能避免这个误区,从第一次作业开始就好好的规划,力求不再重构。另外一点便是要尝试TDD思路,即在Coding之前先构造足够且覆盖面较广的测试集,这样知己知彼,能避免发生后期发现忽略一种情况,但无法在不破坏整体结构的情况下补充进去的窘境。当然,因为我有着做很多事开始前十分犹豫,拖沓的恶习,因此对于我自己来讲还是要权衡好构思的时间范围,毕竟万事开头难,干就完事了!