Adaptive Graph Guided Disambiguation for Partial Label Learning

摘要

偏标记学习的目的是从训练样本中引出多分类器，其中每个训练样本都与一组候选标记相关联，每组候选标记中只有一个是真实标记。训练预测模型的常用策略是消歧，即区分每个候选标记的模型输出，以恢复真实标记信息。近年来，基于特征空间的图结构，提出了基于特征感知的消歧方法，在候选标记集上产生不同标记的置信度。然而，由于训练数据中存在噪声和离群点，使得从原始特征导出的相似性不那么可靠。为此，我们提出了一种基于自适应图引导消歧的偏标记学习方法(PL-AGGD)。相比固定图，自适应图鲁棒性更强，且能更准确地揭示数据内部的流形结构。此外，与以往算法中的两阶段策略不同，我们的方法同时执行标记消歧和预测模型训练。具体而言，我们提出了一个统一的框架，它联合优化真实标记置信度、相似图和模型参数，以获得较强的泛化性能。广泛的实验表明，PL-AGGD相比最先进的部分标记学习方法有很好的效果。

关键词：偏标记、自适应图、消歧

---

介绍

多分类在许多实际应用中是一个重要的问题，比如自然语言处理，计算机视觉，网络广告等。在普通的多分类任务中，每个训练样本和一个标识样本属于哪个类的标记相关联。尽管从这类监督数据集中学习很有效，然而收集标记数据代价昂贵，是实际分类任务的关键瓶颈。因此，在过去的几十年里，人们广泛地研究了从较便宜的标记数据中学习。

偏标记学习旨在从训练样本中引出多分类器，其中每个训练样本都与一组候选标记相关联，每组候选标记中只有一个是真实标记。这个学习问题的动机是在使用大量模糊标记样本的领域中，获取明确的标记代价很高，并且在许多实际的任务中也会出现。 例如自动图像标注，网络挖掘，生态信息学等。

形式上说，令$X={\mathbb{R}}^d$表示d维特征空间$Y=\{0,1{\}}^q$是有q个可能类标记的标记空间。

假设有偏标记训练集$D=\{(x_i,S_i)|1\le i\le m\}$，其中$x_i\in X$是d维特征向量，$S_i$是对应的候选标记集。

偏标记学习任务基于训练集D引入多分类器$g:X\to Y$。偏标记学习框架的基本假设$x_i$在$S_i$中的真实标记$y_i$在训练阶段中算法不可访问。

偏标记学习的常用策略是消歧。即区分每个候选标记的模型输出，以恢复真实标记信息。消歧策略主要分为两种：基于平均的消歧、基于辨识的消歧。对于基于平均的消歧，平等对待每个样本的所有潜在标记都被，并平均模型输出得到预测结果。对于基于辨识的消歧，将真实标记看作潜在变量，并通过迭代筛选程序进行识别。

最近，特征感知消歧方法使用图结构或特征空间对候选标记集生成不同的标记置信度。为了方便消歧过程，特征感知消歧使用了平滑假设，即特征空间中彼此相近的样本将倾向于在标记空间里共享相同的标记。"Partial label learning via feature-aware disambiguation"中提出的方法分为两个阶段，首先在候选标记集中生成潜在的标记置信度，然后利用生成的标记置信度拟合多输出回归器以学习多分类模型。

虽然该论文的结果显示了特征感知消除偏标记学习歧义的有效性，但该策略的一个潜在缺点是，真实数据总是包含大量的噪声和异常值，使得原始特征获得的相似图不那么可靠。本文提出基于自适应图引导消歧（PL-AGGD）的偏标记学习新方法。相比固定图，自适应图鲁棒性更强，且能更准确地揭示数据内部的流形结构。此外，与以往算法中的两阶段策略不同，我们的方法同时执行标记消歧和预测模型训练。在此基础上，我们提出了一个统一的框架，实现了基于交替过程的真实标记置信度、相似度图和模型参数的联合优化。在受控UCI数据集和真实世界的部分标签数据集上的大量实验表明，PL-AGGD优于其他先进的部分标签学习方法。

---

相关工作

在偏标记学习中，训练样本的真实标签在其候选标记集中，算法在训练阶段无法访问。因此，偏标记学习可以看作是一个标记信息模糊的弱监督学习框架。

为了更好地理解偏标记学习问题，有必要说明几个相关地学习场景，包括半监督学习、多样本学习、多标记学习和多样本多标记学习。

• 在半监督学习中，训练样本要么被明确标记，要么没有标记。而在偏标记学习中，训练样本被偏标记。
• 在多样本学习中，样本不是单独标记地，而是分组到包中。而在偏标记学习中，标记是按单个样本分配的。
• 在多标记学习中，每个样本都被分配了多个有效标记。而在偏标记学习中，给样本分配的是一组候选标记。
• 多样本多标记学习可以看作是多样本学习和多标记学习的广义版本。其中训练样本不仅与多个样本相关联，还与多个标记相关联。偏标记学习忽略任何袋结构，独立查看每个样本。而每个多样本多标记的样本可以通过将分配的类标记作为袋中每个样本的候选标记以转化为多个偏标记样本。

尽管基于平均的策略直观且易于实现，它的有效性在很大程度上受到假阳性标签的影响，这些标签的输出将超过真标记所产生的输出。因此，另一种策略是通过识别真实标记来消除候选标签集的歧义。遵循这一策略的现有方法都以真实标记为潜在变量，通过${\hat{y}}_i=\underset{y\in S_i}{\mathrm{argmax}}{g}_y(x_i,W)$识别。一般情况下，潜在变量和模型参数:

• 通过EM过程根据最大似然准则对目标函数进行迭代优化：${\sum }_{i=1}^{m}log(\sum _{y\in S_i}{g}_y(x_i,W))$
• 或者根据最大间隔准则优化：${\sum }_{i=1}^m(\underset{y\in S_i}{\max }{g}_y(x_i,W)-\underset{y\in ̸S_i}{\max }{g}_y(x_i,W))$。

基于辨识的消歧策略的一个潜在缺点是，所标识的标记可能是候选标记集中的假阳性标签，而不是真实标签。

最近提出的特征感知消歧策略利用特征空间中的局部流形结构来帮助候选标签集消歧，这与基于均值和基于身份的消歧策略都有所不同。该策略的一个潜在缺点是，实际数据往往受到显著噪声和异常值的污染，使得从原始特征空间恢复的流形结构不那么可靠。

---

提出的方法

在本节中，我们将介绍所提议的PL-AGGD方法。我们首先提出了一个统一的框架，旨在同时进行消歧、自适应图优化和模型学习。在此基础上，引入了一种有效的优化方法来处理该框架。

自适应图引导消歧

令$X=[x_i,x_2,...,x_m{]}^T\in {\mathbb{R}}^{m\times d}$为特征矩阵.

$Y=[y_1,y_2,...,y_m{]}^T\in \{0,1{\}}^{m\times q}$为偏标记矩阵，其中$y_{ij}=1$表示$x_i$的第j个候选标记。

给定训练集D，通过训练样本构建加权图$G=(V,\epsilon ,S)$，
其中:

• $V=\{x_i|0\le i\le m\}$对应顶点集，
• $\epsilon =\{(x_i,x_j)|x_i\in KNN(x_j),i≠j\}$对应$x_i$到$x_j$的边集，$x_i$是$x_j$的k近邻。
• $S\in {\mathbb{R}}^{m\times m}$对应非负权重矩阵，其中若$(x_i,x_j)\in ̸\epsilon$则$s_{ij}=0$

对于每个训练样本$(x_i,S_i)$，计划生成正则化实值向量$f_i\in {\mathbb{R}}^q$，其中$f_{il}$表示第l个标记是$x_i$的真实标记的置信度。标记置信度向量$f_i$满足以下约束：

1. $\sum _{y_{il}=1}{f}_{il}=1$
2. $f_{il}\ge 0(\forall y_{il}=1)$
3. $f_{il}=0(\forall y_{il}=0)$

这里，第二个约束意味着潜在的真实标签位于候选标签集中，第三个约束保证每个非候选标签的标签置信度必须为0。生成正则化标记置信度向量后，将原偏标记训练集D转化成消歧训练集：$\tilde{D}=\{(x_i,f_i)|1\le i\le m\}$。基于消歧结果$\tilde{D}$进行多输出回归，引入预测模型。

特征识别消歧是利用特征空间的图结构来区分候选标签集的。具体而言，通过求解以下线性最小二乘问题(1)，构造相似图权矩阵S:
$$\underset{S}{\min }\sum _{j=1}^m||x_j-\sum _{(x_i,x_j)\in \epsilon }{s}_{ij}{x}_i|{|}_2^2$$ $$s.t.S{1}_m=1_m,s_{ij}\ge 0(\forall (x_i,x_j)\in \epsilon ,s_{ij}=0(\forall (x_i,x_j)\in ̸\epsilon ))$$

其中$1_m$是大小为m的全1向量。

然后，利用特征空间中的流形结构也应保留在标记空间中的平滑假设，标记置信度矩阵$F=[f_1,f_2,...,f_m{]}^T\in {\mathbb{R}}^{m\times q}$可求解以下问题(2)获得：
$$\underset{F}{\min }\sum _{j=1}^m||f_j-\sum _{(x_i,x_j)\in \epsilon }{s}_{ij}{f}_i|{|}_2^2$$$$s.t.F{1}_q=1_m,f_{il}\ge 0(\forall y_{il}=1),f_{il}=0(\forall y_{il}=0)$$

在以往的特征感知消歧中，问题(1)和问题(2)是单独求解的，因此消歧过程是由固定图引导。由于噪声和离群点的广泛存在，固定相似图揭示数据内部结构是很有挑战的工作，因此考虑使用自适应相似加权矩阵。同时得到相似加权矩阵和区分标记置信度以得到更好的分歧结果。通过联合解决问题(1),(2)，相似图权重不仅由特征的距离信息决定，并基于标记空间的反馈调整。相比固定图，自适应图会更具有鲁棒性且更准确。

此外，同时执行标记消歧和预测模型训练，以代替之前算法的两步策略（先消歧，再引入模型）。因此标记置信度可以通过流形假设和模型输出优化。我们提出了一个统一框架，共同优化标记置信度、相似权重和预测模型，以获得较强的泛化性能。将模型参数表示为矩阵$W\in {\mathbb{R}}^{d\times q}$，使用最小二乘损失(3)优化预测模型：
$$l(g(x_i,W),f_i)=||g(x_i,W)-f_i|{|}_2^2$$我们采用广泛使用的平方Frobenius范数作为正则项控制模型复杂度。则目标函数（4）如下：
$$\underset{S,F,W}{\min }=\sum _{j=1}^m|g(x_i,W)-f_i{|}_2^2+\mu \sum _{j=1}^m||f_j-\sum _{(x_i,x_j)\in \epsilon }{s}_{ij}{f}_i|{|}_2^2+\gamma \sum _{j=1}^m||x_j-\sum _{(x_i,x_j)\in \epsilon }{s}_{ij}{x}_i|{|}_2^2+\lambda ||W|{|}_F^2$$$$s.t.S{1}_m=1_m,0_{m\times m}\le S\le N,F{1}_q=1_m,0_{m\times q}\le F\le Y$$其中：

• $N\in \{0,1{\}}^{m\times m}$定义为： 若$(x_i,x_j)\in \epsilon$，$n_{ij}=1$；否则$n_{ij}=0$
• $0_{m\times m}$是$m\times m$的全0矩阵
• $\lambda$是正则化参数
• $\mu ,\gamma$是标签和特征空间重建损失的权衡参数。

交替优化

因为问题（4）包含三组不同正则化和约束的变量，很难直接解决。我们采用替代优化方法解决这个问题：我们通过固定其他变量组迭代优化每个变量集，直到收敛或达到最大迭代次数为止。

更新S：通过固定F和W，优化问题（4）可表述如下（5）：
$$\underset{S}{\min }\mu \sum _{j=1}^m||f_j-\sum _{(x_i,x_j)\in \epsilon }{s}_{ij}{f}_i|{|}_2^2+\gamma \sum _{j=1}^m||x_j-\sum _{(x_i,x_j)\in \epsilon }{s}_{ij}{x}_i|{|}_2^2$$$$s.t.S{1}_m=1_m,0_{m\times m}\le S\le N$$

每个样本的相似矩阵是独立的，因此固定其他变量，并逐个优化相似矩阵。这里从单个样本j考虑以上问题，如（6）所示：
$$\underset{S_j}{\min }\mu \sum _{j=1}^m||f_j-\sum _{(x_i,x_j)\in \epsilon }{s}_{ij}{f}_i|{|}_2^2+\gamma \sum _{j=1}^m||x_j-\sum _{(x_i,x_j)\in \epsilon }{s}_{ij}{x}_i|{|}_2^2$$$$s.t.S_j^T{1}_m=1,0_m\le S_j\le N_j$$

注意到对于$S_j$，只有k个非负元素需要更新。令${\hat{s}}_j\in {\mathbb{R}}^k$表示相似权重向量，其中每个元素是代表邻居样本在重构$x_j$的相对重要性。

令$$D^{f_j}=[f_j-F_{N_j(1)},f_j-F_{N_j(2)},...,f_j-F_{N_j(k)}{]}^T\in {\mathbb{R}}^{k\times q}$$

$$D^{x_j}=[x_j-x_{N_j(1)},x_j-x_{N_j(2)},...,x_j-x_{N_j(k)}]\in {\mathbb{R}}^{k\times d}$$

则优化问题（6）可重写为（7）：
$$\underset{\widehat{s_j}}{\min }{\widehat{s_j}}^T(\mu G^{f_j}+\gamma G^{x_j})\widehat{s_j}$$$$s.t.{\hat{s}}_j^T{1}_k=1,0_k\le \widehat{s_j}\le 1_k$$其中 $G^{f_j}=D^{f_j}(D^{f_j}{)}^T\in {\mathbb{R}}^{k\times k}$ 和 $G^{x_j}=D^{x_j}(D^{x_j}{)}^T\in {\mathbb{R}}^{k\times k}$ 是分别对应标记空间和特征空间的Gram矩阵。优化问题（7）是k个变量的标准二次规划（QP）问题，可以通过现有的QP工具有效解决。求解出每个$\widehat{s_i}$后,将它们集中起来获得更新的图矩阵S。

更新F：固定S和W，优化问题（4）可以表述如下（8）：
$$\underset{F}{\min }||H-F|{|}_F^2+\mu \sum _{j=1}^m||f_j-\sum _{(x_i,x_j)\in \epsilon }{s}_{ij}{f}_i|{|}_2^2$$$$s.t.F{1}_q=1_m,0_{m\times q}\le F\le Y$$其中$F=[f_1,f_2,...,f_m{]}^T\in {\mathbb{R}}^{m\times q}$，$H\in {\mathbb{R}}^{m\times q}$表示模型输出矩阵。

令$\tilde{f}=vec(F)\in [0,1{]}^{mq}$，其中$vec(\cdot )$是向量化运算符。同样的，$\tilde{h}=vec(H)\in [0,1{]}^{mq}$, $\tilde{y}=vec(Y)\in [0,1{]}^{mq}$。

定义方阵$T=S{S}^T+(S^T{1}_{m\times m}S)⨀I_{m\times m}-2W+\frac{1}{\mu }{I}_{m\times m}$其中$⨀$是哈达玛乘积，$I_{m\times m}$是m行m列的单位矩阵。则优化问题（8）可写成（9）：
$$\underset{\tilde{f}}{\min }\frac{1}{2}{\tilde{f}}^T(\Lambda +{\Lambda }^T)\tilde{f}-\frac{2}{\mu }{\tilde{h}}^T\tilde{f}$$$$s.t.0_{mq}\le \tilde{f}\le \tilde{y},\sum _{j=1,j\%m=i}^{mq}\widetilde{f_j}=1(\forall 0\le i\le m-1)$$其中$\Lambda \in {\mathbb{R}}^{mq\times mq}$，定义如下(10)：
$$\left[\begin{array}{cccc}T& 0_{m\times m}& \cdots & 0_{m\times m}\\ 0_{m\times m}& T& \cdots & 0_{m\times m}\\ ⋮& \ddots & \ddots & ⋮\\ 0_{m\times m}& \cdots & 0_{m\times m}& T\end{array}\right]$$优化问题（9）也符合标准二次规划问题，可通过当前QP工具解决。问题（9）的第二个约束使用QP工具时可以使用矩阵形式实现。具体地，令$B=[I_{m\times m},I_{m\times m},...,I_{m\times m}]\in \{0,1{\}}^{m\times mq}$,则约束可表示为$B\tilde{f}=1_m$。注意到该QP问题有mq个变量和m(q+1)个约束，因此mq较大时，计算复杂度非常高。我们遵循"Partial label learning via feature-aware disambiguation"，对大型数据集采用交替优化策略。对于标记置信向量$f_j$，可以通过固定所有其他标记置信度向量对其进行优化（11）：
$$\underset{f_j}{\min }(t_{jj}+\frac{1}{\mu })f_j^T{f}_j+(\sum _{i=1,i≠j}^m(t_{ij}+t_{ji})f_i^T-\frac{2}{\mu }{h}_i^T)f_j$$$$s.t.0_q\le f_j\le y_j,f_j{1}_q=1$$现在问题（9）转换成q个变量q+1个约束一系列QP子问题，可以更有效的求解。

更新W：固定F和S，使用简单的线性模型$g(x_i,W)=W^T{x}_i$，问题（4）可以表述如下(12):
$$\underset{W}{\min }\sum _i||W^T{x}_i-f_i|{|}_2^2+\lambda ||W|{|}_F^2$$这种正则化最小二乘问题很简单，可以通过梯度下降法轻松解决。

为了使预测模型获得更好的性能，对于一般的线性情况，可以进一步促进核扩展。令$\varphi (\cdot ):{\mathbb{R}}^d\to {\mathbb{R}}^h$表示特征映射，将特征空间映射到h维的高维希尔伯特空间。用核扩展的预测函数可表示为$g(x_i,W)=W^T\varphi (x_i)$。那么有了以下的问题（13）：
$$\underset{W}{\min }\sum _i||{ϵ}_i|{|}_2^2+\lambda ||W|{|}_F^2$$$$s.t.f_i=W^T\varphi (x_i)-{ϵ}_i$$通过定义矩阵$E=[{ϵ}_1,{ϵ}_2,...,{ϵ}_m{]}^T\in {\mathbb{R}}^{m\times q}$，以上问题可写成以下矩阵形式（14）：
$$\underset{W}{\min }tr(E^{T}E)+\lambda tr(W^{T}W)$$$$s.t.F=\Phi W-E$$其中$\Phi =[\varphi (x_1),\varphi (x_2),...,\varphi (x_m){]}^T$，该问题的拉格朗日函数为（15）：
$$L=(W,E,A)=tr(E^{T}E)+\lambda tr(W^{T}W)-tr(A^T(\Phi W-E-F))$$其中$A\in {\mathbb{R}}^{m\times q}$存储拉格朗日乘子。问题（15）的最优解需要满足以下条件（16）：
$$\frac{\partial L}{\partial W}=2\lambda W-{\Phi }^{T}A=0$$$$\frac{\partial L}{\partial E}=2E+A=0$$$$\frac{\partial L}{\partial \Psi }=\Phi W-E-F=0$$从以上线性方程组得到（17）：
$$W=\frac{{\Phi }^{T}A}{2\lambda }$$$$A=(\frac{1}{2\lambda }K+\frac{1}{2}{I}_{m\times m}{)}^{-1}F$$ 其中元素$k_{ij}=k(x_i,x_j)$的矩阵$K=\Phi {\Phi }^T$基于对应核函数$k(\cdot ,\cdot )$。对于PL-AGGD，采用高斯核函数$k(x_i,x_j)=exp(-\frac{||x_i-x_j|{|}_2^2}{{\sigma }^2})$，$\sigma$为每对训练样本之间的平均距离。然后通过合并特定的核函数，模型输出矩阵定义为$H=\Phi W=\frac{1}{2\lambda }KA$。此外，此方法获得的测试样本x的预测标记为（18）：
$$y^{\ast }=arg\underset{k}{\min }\sum _{i=1}^m{a}_{ik}k(x,x_i)$$PL-AGGD的伪代码总结为表1：

可以看到，方法的第一个过程是初始化S和F(步骤2-4)，采用特征感知消除歧义。然后采用交替优化策略学习自适应图，指导标签消歧(步骤5-12)，同时训练预测模型。最后，根据所学习的模型对未见过的样本进行分类(步骤13)。

实验

实验设计

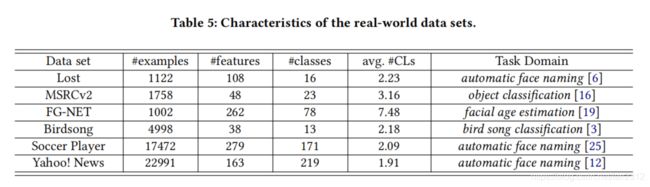
在本节中，我们基于受控UCI数据集以及真实偏标记数据集进行两个系列的对比实验。 受控UCI数据集和真实数据集的特征分别总结在表2和表5中。

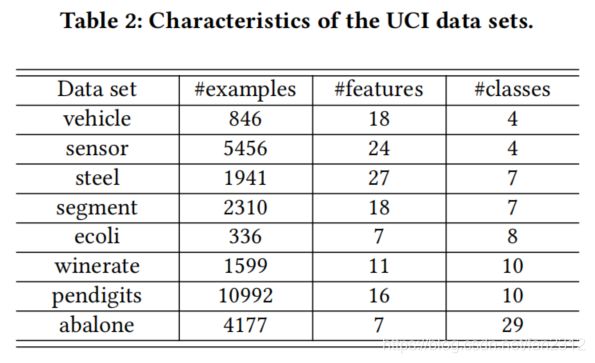
遵循以往偏标记学习研究中广泛使用的控制协议，可使用控制参数$p,r,ϵ$从多累UCI数据集生成人工偏标记数据集。p控制偏标记的样本比例（在所有实验中设置p=1），r控制候选标记集中的假阳性标记数量（即$|S_i|=r+1$）。在我们的设置中，训练集的模糊标记是在不替换的情况下生成的。$ϵ$是模糊度，控制一个耦合候选标记和真实标记之间的共存概率。这是通过首先为每个标签随机选择主要共现标签，即通过概率ε采样，然后以概率$\frac{1-ϵ}{L-2}$均匀采样其余标签来实现的(每个样本都有一个额外的标签)。

除了人工数据集之外，还从几个任务领域收集了一些真实偏标记数据集(见表5)，包括:人类自动命名领域的Lost, Soccer Player, Yahoo! News；目标分类领域的MSRCv2；面部年龄估计领域的FG-NET；鸟鸣分类的BirdSong。

• 对于自动人脸命名任务，从图像或视频中裁剪的人脸被表示为样本，而从相关标题或字幕中提取的名称被视为候选标签。
• 对于目标分类任务，图像分割被表示为样本，而出现在同一图像中的目标被视为候选标记。
• 对于面部年龄估计任务，带有标记点（landmark）的人脸表示为样本，由十个众包标注者标注的年龄和真实年龄作为候选标记。
• 对于鸟鸣分类任务，以鸟的发声音节作为样本，以鸟类在10秒内共同发声为候选标记。

采用5种最先进的偏标记学习算法，每种算法采用各自文献建议的超参设置：

• PL-KNN：一种基于k近邻的偏标记学习方法，实现了基于平均的消歧[建议设置：k=10]；
• CLPL：基于凸学习公式的平均消歧方法，在偏标记环境下最下滑凸损失函数[建议设置：带平方铰链损失的支持向量机]；
• PL-SVM：一种使用最大间隔法的偏标记学习方法，进行基于辨识的消歧[建议设置：正则化参数池{0.01, 0.1, 1, 10, 100}]；
• LSB-CMM：一种使用最大自然法的偏标记学习方法，进行基于辨识的消歧[建议设置：混合组件(mixture component)=q]；
• PL-LEAF：基于特征感知消歧的两阶段方法$[k=10,C_1=10,C_2=1]$。

对于PL-AGGD,参数设置为$k=10,T=20,\lambda =1,\mu =1,\gamma =0.05$。对于每个人工及真实偏标记数据集按50%/50%随机进行训练集/测试集的分割，记录所有算法运行10次的平均精度（标准差）。

实验结果

受控UCI数据集 图1说明了在共同出现概率$ϵ$从0.1到0.8以步长0.1变化的条件下，每个进行比较的算法在受控UCI数据集上的分类精度。对于任何真实标记$y\in Y$，指定一个额外的标记$y^{\prime }≠y$为和y在候选标记集中以概率$ϵ(r=1)$共同出现的耦合标记。

在表3中，我们改变了模糊的大小：与每个样本的关联的额外标记数量。例如，对于每个样本，除了真实标签外，还将随机选取r个额外的类标签组成候选标签集。

如表3和图1所示，PL-AGGD相比其他算法具有更优或可比的性能。所有8个UCI数据集的75个统计测试（表3中有23种设置，表4中有52种设置）显示：

• 与基于平均的消歧方法相比，在大多数情况下，PL-AGGD比PL-KNN和CLPL具有更好的性能。
• 相比基于辨识的分歧方法，PA-AGGD分别在86.7%和72%的例子中优于PL-SVM和LSB_CMM。此外，PL-AGGD的性能仅比LSB-CMM差1例，而PL-SVM的性能仅在4例中优于LSB-CMM。
• 与现有特征感知方法PL-LEAF相比，PL-AGGD在56%的例子中拥有更好的性能，仅5例优于PF-LEAF。而且，从图1和表3中可以观察到PL-AGGD当模糊度或模糊大小很高时的鲁棒性更好。
  
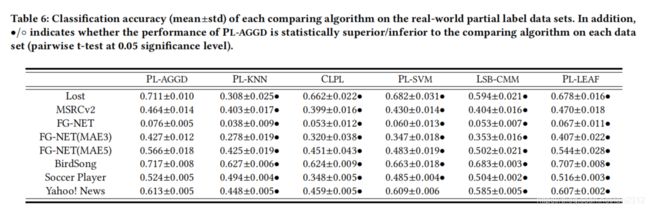
  真实数据集 ：表6显示了每个进行比较的算法在真实偏标记数据集上的分类准确性。注意到FG-NET的数据集的平均候选标签数非常大，这会使得基于偏标记训练样本的每个算法的分类精度非常低。该任务的常用评估标准是预测年龄和真实年龄之间的平均误差（MAE）。在表6中，为了更好地评估该面部年龄估计任务，对FG-NET数据集进行了两个额外的实验，若预测年龄与实际年龄之间的差值不超过3年或者5年，则样本被正确分类。

如表6所示，显然PL-AGGD相对其他所有算法在除了Yahoo！News、PL-LEAF真实数据集上性能更优。而且我们的方法没有被其他任何方法超过。

深入分析

转换精度：除了如表6所示的转换精度，研究每种比较算法在分类训练样本时的转换性能也很有趣。偏标记学习的转换性能反映了其对候选标签集的消歧能力。对于PL-AGGD和PL-LEAF，生成的标签置信度向量$f_i$被用于训练样本$x_i$的真实标签：${\hat{y}}_i=arg\underset{y_k\in S_i}{\max }{f}_{ik}$对于其他方法，通过参考候选标签集$S_i$来预测真实标签，即，${\hat{y}}_i$为预测模型的最大输出。

因此，表7报告了每种比较算法的转换准确度以及显著性水平为0.05的成对t检验结果。在40个统计测试中（8个数据集×5个比较算法），发现：

• 与基于平均的消歧方法相比，PL-AGGD在FG-NET数据集上优于PL-KNN，在Lost和FG-NET数据集上优于CLPL。在其余的统计测试中，PL-AGGD性能优于或至少相当于PL-KNN和CLPL。
• 与基于辨识的消歧方法相比，PL-AGGD在Yahoo!News数据集上表现优于PL-SVM。在其余的统计检验中，PL-AGGD的表现优于或至少与PL-SVM和LSB-CMM相当.
• 与现有特征感知方法PL-LEAF相比，PL-AGGD拥有更好或可比的性能

参数敏感度：在这里讨论PL-AGGD的三个参数$\lambda ,\mu ,\gamma$的灵敏度。

如图2(a)和图2(b)显示，当 $\mu$较小（这意味着在更新F时，标签空间的流形信息很难被利用）的时候，PL-AGGD的性能较差。当$\mu$增加的时候，PL-AGGD开始考虑流形信息，分类性能增加。然而，若$\mu$过大，分类精度会急剧下降。对于$\lambda$，当它太小或太大时，性能也会处于较低的水平。在实践中，建议$\mu ,\lambda$设置为近似1.另一个是用以控制模型复杂度的权衡参数$\gamma$。图2©显示随$\gamma$变化的分类精度曲线表明在过拟合和欠拟合之前权衡的重要性。在实践中，可以在训练前手动搜索。

图2(d)以两个相邻迭代间的标记置信矩阵的差（通过l2范数$||F^{(t)}-F^{(t-1)}|{|}_F^2$）绘制PL-AGGD的收敛曲线。可以看到标记置信度分数随着迭代次数的增加而收敛。

总结

本文研究了偏标记学习问题，提出了一种基于自适应图引导消歧的偏标记学习法。本文提出的PL-AGGD方法不采用固定相似度图作为先前的特征识别消歧策略，而是通过同时进行标签消歧和预测模型训练，从部分标签示例中学习。大量的对比研究清楚地证明，自适应图导消歧能够更加鲁棒和准确地揭示数据内部的流形结构。

该方法从原始特征空间中挖掘流形结构，将特征嵌入技术集成到PL-AGGD可获得更好的性能。此外，对半监督学习、不完全多标签学习等弱监督学习环境下的自适应图的研究也有一定的参考价值