一、三次作业分析
1. 第一次作业
1.1 需求分析
第一次作业的需求是完成简单多项式导函数的求解,表达式中每一项均为简单的常数乘以幂函数形式。为取得性能分,需要优化目标为最短输出。为了满足优化目标,我们需要将含有相同指数的项进行合并。
1.2 实现方案
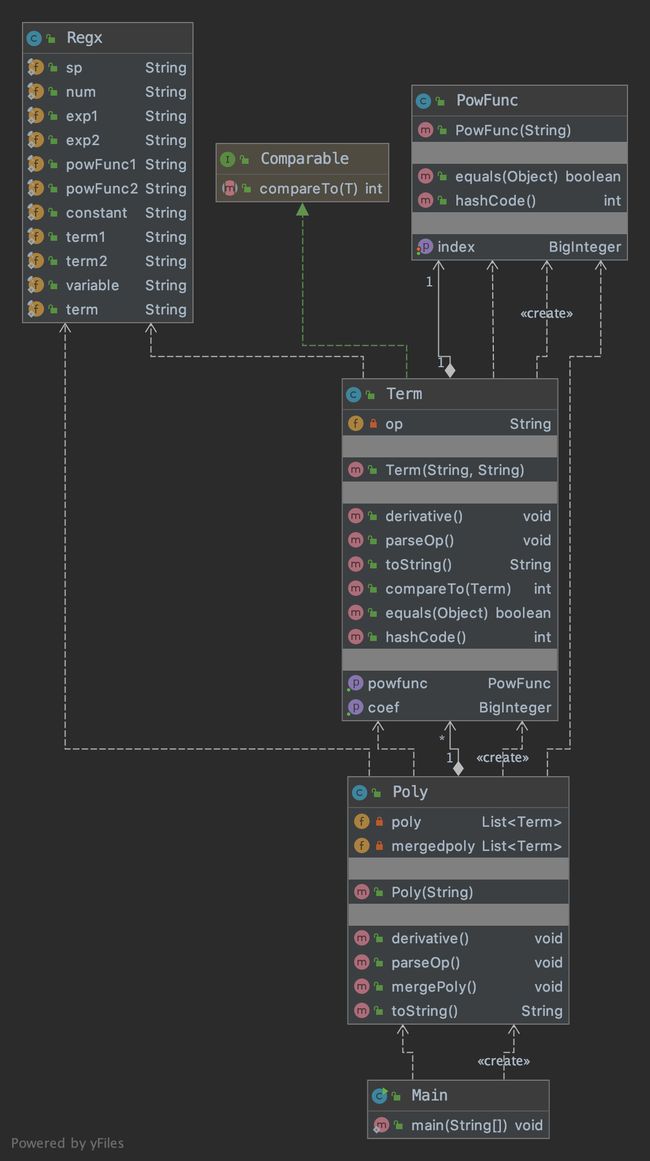
根据需求,我们很容易就能想到利用ArrayList构建多项式,存储每一个项,于是建立了Poly多项式类和Term项类,并利用Poly类中的属性ArrayList进行表达式的存储。由于第一次作业不需要进行输入表达式的格式判断,直接用正则表达式匹配输入字符串即可。
多项式求导程序具体实现中的步骤分为:输入串处理、求导、同类项合并,以及表达式输出。
在本程序中对于输入串的处理仅仅利用了Poly类的构造函数Poly(String str),由于本次作业中每一项仅仅为系数和幂函数的组合,故可以对照指导书轻松写出每一项的正则表达式,利用正则表达式的捕获组解析出每一个项,项内同样利用捕获组解析出系数和指数,就完成了多项式的存储。在求导时,对于ArrayList的每一项遍历进行求导产生新项是非常简单的,最终返回一个新的Poly。然后利用HashMap进行同类项合并,指数作为key,系数作为value。遍历ArrayList将项存入HashMap中,如果不存在则对应系数置为1,如果已经存在则进行系数相加。输出时,重写多项式类和项类的toString()方法,并且注意跳过0项的输出,如果最后得到输出字符串为空串,则输出0。为了得到所有性能分,还要注意把正项(如果有的话)放在第一个输出,并且略去正号。因此我还重写了Term的compareTo()方法,以实现系数从大到小排序。
程序UML图如下:
1.3 基于度量的结构分析
此次作业中,解决关键问题的仅有Poly类中的Poly()(输入处理)、derivative()(求导)、mergePoly()(合并同类项)、toString()(输出)。
本次作业的度量如下:
| 指标 | 平均值 | 总值 | 特殊值 |
|---|---|---|---|
| Lines of Code(总行数) | 46.20 | 246 | Term - 121 |
| Lines of Code Method(方法行数) | 10.15 | 203 | Term.Term(String,String) - 44 |
| Essential Cyclomatic Complexity(基本复杂度) | 1.70 | 34 | Term.toString() - 8 |
| Design Complexity(设计复杂度) | 2.30 | 46 | Term.toString() - 8 |
| Cyclomatic Complexity(循环复杂度) | 3.15 | 63 | Term.toString() - 16 |
| Average Operation Complexity(平均操作复杂度) | 2.70 | Term - 3.56 |
|
| Weighted Method Complexity(加权方法复杂度) | 10.80 | 54 | Term - 32 |
| Cyclic Dependencies(循环依赖) | 0 | ||
| Depth of Inheritance Tree(继承树深度) | 1 |
通过上面的度量结果可以发现,Term类复杂度问题很大,代码行数达到了121行,并且带来了很大的复杂度。其中构造方法Term.Term(String,String)行数最多,但得益于采用了正则表达式来处理输入的字符串,所以虽然看上去行数多,但复杂度反而不是很高。对于Term.toString()方法,由于存在很多if...else分支条件语句来进行输出化简,其复杂的优化逻辑让复杂度变得相当大。本次没有出现循环依赖。由于Term类继承了Comparable类,所以继承树深度为1。
1.4 自己程序的bug
由于第一次作业的代码逻辑较为简单,只是初步接触java的OO思想,所以Debug没有给我留下什么深刻印象。第一次作业我在强测中拿到了100分,互测也没有被别人hack,可以说第一步还是比较成功的。需要注意一点是,用正则表达式匹配项时,由于变量项也有系数的存在,而正则表达式有 ‘|’ 的情况下,匹配时是从左向右匹配的,所以一定要把变量项写在常数项前面匹配。测试的思路也并不复杂,只需要按照指导书对每一种不同的省略输入进行测试即可。
2. 第二次作业
2.1 需求分析
第二次作业需要完成简单幂函数和简单正余弦函数求导,在第一次作业的基础上增加了sin(x)和cos(x)因子,且每一项由若干因子组成,因子之间可以相乘。并且加入了非法输入格式判断,但保证输入字符串空白符位置不会出现非法情况。优化目标依然是最短输出,优化关键有二:合并同类项,利用sin(x)2+cos(x)2=1进行展开或合并。
2.2 实现方案
本次作业新增输入表达式的格式判断,并且由于没有括号嵌套存在,可以比较容易的写出多项式的正则,所以本人直接用正则表达式匹配输入字符串的方法,匹配则为输入合法,否则输出WRONG FORMAT!。
这次作业中仍然利用Poly类中的ArrayList存储多项式的每一个项,利用正则表达式解析每一项和每一个因子。由于新增了sin和cos因子类,所以我创建了一个Factor因子类接口并规定求导和输出方法,PowFactor、SinFactor、CosFactor因子类都继承自接口。对于每个因子类,存储因子类别、系数和指数,为求导时产生带系数的项做准备,并且尝试采用了工厂模式来构建每一个因子。对于项类Term,采用了三元组思想,存储项的系数和三种因子,虽然知道这样的话在增加括号嵌套功能之后一定需要重构,但由于本次作业采用这样的实现方法不论是存储还是合并同类项都比较简单,还是采用了三元组的存储方法。
对于求导处理,在不同的层次采用不同的求导策略:对于各因子类,分因子类型采取不同的求导策略;在Term类中实现各因子的乘法法则;在Poly类中对项遍历,实现加法法则。
对于输出,表达式树的每一层均重写了toString()方法,使得底层只需考虑最简单的单因子输出,而项和表达式仅需将底层传上来的字符串进行符号连接即可,这种分对象进行处理的方式免去了多种情况讨论的复杂逻辑,十分方便且耦合较为简单。
对于合并同类项,我依然对于可合并的项重写equals()和hashCode()方法通过HashMap合并,从而最大限度地合并同类项,不同的是本次key为三种因子指数的三元组,value仍然是系数。
本次作业还新增了一大难点,三角函数化简问题。对于sin(x)和cos(x)的合并问题,该问题是一个仅能寻求近似解的问题:由于可能涉及到项的拆分,所以该任务不能仅由简单的贪心完成,这大大增加了优化成本;讨论区内的DFS+贪心策略虽然可以实现,但对于我来说风险过大,由于性能分仅占20%,正确性依然是首先需要保证的,所以我仅仅实现了最简单的sin(x)2+cos(x)2=1的合并。也因此我的性能分不是很高。
本次作业程序UML图如下:
2.3 基于度量的结构分析
本次作业将三个主要任务下放至三个层次中分别处理该层的对应特征。
本次作业的度量如下:
| 指标 | 平均值 | 总值 | 特殊值 |
|---|---|---|---|
| Lines of Code(总行数) | 59.33 | 566 | Poly - 138 |
| Lines of Code Method(方法行数) | 10.34 | 486 | Term.Term(String,String) - 56 Poly.simplify() - 57 |
| Essential Cyclomatic Complexity(基本复杂度) | 1.60 | 75 | Factory.createFactor(String) - 5 |
| Design Complexity(设计复杂度) | 2.17 | 102 | Poly.simplify() - 12 Term.Term(String,String) - 10 |
| Cyclomatic Complexity(循环复杂度) | 2.79 | 131 | Poly.simplify() - 13 |
| Average Operation Complexity(平均操作复杂度) | 2.45 | Factory - 5 , Term - 3.70 , Poly - 3.57 |
|
| Weighted Method Complexity(加权方法复杂度) | 12.78 | 115 | Term - 37 |
| Cyclic Dependencies(循环依赖) | 0 | ||
| Depth of Inheritance Tree(继承树深度) | 1 |
本次作业在将不同种对象在类中加以区分之后在各项指标的平均值上均出现了下降,这表明面向对象的思路的确可以通过将单一任务区分为不同类对象的分任务的方式降低程序复杂度,同时让编程思路更加清晰。但是,此次OO的思路依然没有贯穿始终,从Poly.simplify()方法的高复杂度就能看出在对三角函数进行化简的时候还是运用了面向过程的思路。Term构造方法和Factory工厂方法中都采用了多重if...else来判断因子类型,所以复杂度也较高。Term类由于加入了很多优化判断方法,故其WMC很高。
2.4 自己程序的bug
本次作业中我犯了一个非常低级的错误。导致强测错了一个点,互测中也是因为这一个bug被hack了7次。
那就是这次作业为了尽可能减小输出长度,可以把幂函数因子的x**2输出为x*x。但是我犯了一个非常低级的错误,我是在Poly类的toString()方法中遍历,把将要输出的x**2全部替换为了x*x,这样原本要输出为x**20的字符串就会被我输出为x*x0,导致输出格式错误。正确方法应该是在PowFactor类的toString()方法中把指数为2的因子进行替换输出,这样就不会引起其他指数的因子的变化。
因为这样的低级失误而被扣分,真的很不应该!
3. 第三次作业
3.1 需求分析
第三次作业加入了表达式和sin/cos因子嵌套。多层嵌套使得表达式树深度大幅度增加,并且也使得我们没办法仅仅通过一个正则表达式来匹配表达式和项。并且取消了输入字符串不会出现空白符位置非法的限制,所以我们还需要判断空白符的位置是否非法。
3.2 实现方案
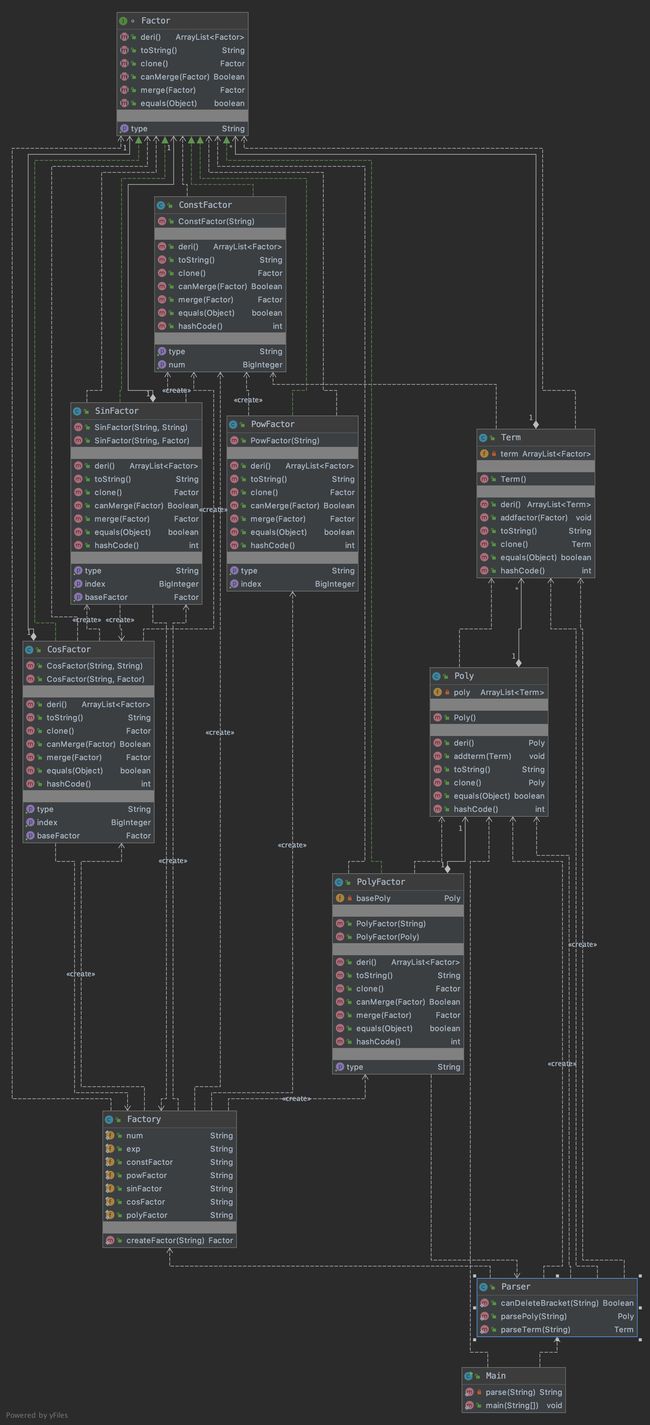
在该任务中,已经很难看到之前作业那种很明显的对应关系,因为因子和项已经可以嵌套,而且可以变得相当复杂。因此,在此次作业中,我将系数构建一种常数因子类ConstFactor,并增加了一种表达式因子类PolyFactor,都实现Factor接口。同样实现了工厂类Factory,把每一类因子的正则表达式作为其属性,让工厂类通过输入的因子字符串逐一匹配并返回对应的因子类型,如果无法匹配则抛出异常。在存储上,表达式类使用了ArrayList
对于输入处理,先进行输入字符串分析以及预处理,包括是否为空/非法字符探测/非法空白符探测等等,并删掉所有空白符。之后在表达式字符串中根据+-截断解析出项,在项字符串中根据*截断解析出因子,并最终给工厂类Factory进行因子匹配,以此构建表达式树。与先前不同的地方在于,此次由于因子内依然可以包含表达式,所以需要在每一次截断时必须使得截断的符号在最外层括号之外。首先遍历输入字符串,并利用栈(此处并不需要维护一个真正的Stack,而是可以利用一个初值为0的数int stack通过加1和减1操作模拟压栈和弹栈)维护当前字符处的括号情况,当栈为空(即当前符号不在任何一对括号内)且当前字符为需要截断的字符时,向其之前增加一个特殊字符作为标记,在遍历完成后根据该特殊字符进行截断进行下一层分析。对于表达式因子类中表达式的提取,只需要利用String.substring(1,str.length()-1)将外层的两个括号去掉,传给PolyFactor类即可。在任何一步中出现正则表达式无法匹配的情况,都抛出异常,由函数逐层传给其调用函数,直至抛给main()进行错误输出。这样的匹配模式不需要一个统一的输入处理类,而是由各个类自己利用构造器根据输入字符串构造属于自己的对象,将任务进行了分派,更符合面向对象的思想。
对于求导处理,此次的实现更为清晰:在因子类中实现链式法则,在项类中实现乘法法则,在表达式类中实现加法法则。求导的结果最终会由表达式树的低端依次向上传递,直至传递到最高层的Poly中。
对于输出处理,同样分派给各个类去实现自己的toString()函数,由低端向上传递。这样可以将输出的优化尽可能分散开,也便于查找错误。
对于优化,此次由于可以嵌套,三角函数优化的难度过大(几乎不太可能),所以并没有实现有关sin/cos的优化。然而,此次依然进行了合并同类项以及合并同类因子的操作。合并同类因子的操作:在Term类中实现addfactor(Factor)方法,每次向项类的ArrayList中add因子时,先遍历整个ArrayList,查看是否有可以合并的因子,有则进行因子合并。在Factor接口定义boolean CanMerge(Factor)方法判断两个因子是否可以合并,同类型的因子可以根据乘法合并,同时定义Factor Merge(Factor),就是每个因子合并的时候调用的函数,返回值是合并后的Factor。合并同类项:每次向表达式类的ArrayList中add项时,也遍历整个ArrayList,查看是否有可以合并的项。与上面的方法类似。
本次作业程序UML图如下:
3.3 基于度量的结构分析
本次作业的度量如下:
| 指标 | 平均值 | 总值 | 特殊值 |
|---|---|---|---|
| Lines of Code(总行数) | 79.2 | 827 | Term - 117 |
| Lines of Code per Method(方法行数) | 10.15 | 751 | Factory.createFactor(String) - 59 , Term.toString() - 56 |
| Essential Cyclomatic Complexity(基本复杂度) | 1.95 | 144 | Factory.createFactor(String) - 11 , Term.toString() - 11 |
| Design Complexity(设计复杂度) | 2.11 | 156 | Term.toString() - 16 , Parse.parsePoly(String) - 11 , Parse.parseTerm(String) - 11 |
| Cyclomatic Complexity(循环复杂度) | 2.62 | 194 | Term.toString() - 17 , Factory.createFactor(String) - 12 , Parse.parsePoly(String) - 12 , Parse.parseTerm(String) - 11 |
| Average Operation Complexity(平均操作复杂度) | 2.32 | Factory - 12.00 , Parser - 8.33 , Term - 4.43 |
|
| Weighted Method Complexity(加权方法复杂度) | 17.20 | 172 | Term - 31 |
| Cyclic Dependencies(循环依赖) | 2 | ||
| Depth of Inheritance Tree(继承树深度) | 1 |
在加入了括号嵌套的功能后,本次作业在各项复杂度指标上仍然和上次作业差不多,这表明对于各个类的功能分拆取得了成效。Term类作为联系表达式和因子的桥梁,其WMC值较高也是有一定道理的。在方法的复杂度上,所有经过了字符串遍历用栈来维护括号对应的方法复杂度都较高,因为其中出现了一些较多的判断条件,无法避免。实际上,可以通过更巧妙的办法,比如讨论区中提到的把最外层括号替换成方括号[...]然后用正则匹配的拆分项和因子的方法,可以减少用栈遍历字符串的次数,降低复杂度。工厂类Factory中Factory.createFactor(String)方法的行数和复杂度都较高,完全可以通过一些操作的拆分来分配任务,减少复杂度。
3.4 自己程序的bug
本次作业中出现的问题就比较多了,首先因为我对字符串输入预处理的一个只写了sin而漏写了cos的小失误,导致强测中WRONG FORMAT判断错了两个点。其次因为我在表达式因子PolyFactor的toString()方法中对于可以省略输出外层括号的条件判断错误,导致被hack。这都是某一个具体的方法中因为手抖而不小心写错导致的bug。
除此之外,还有一个重大的问题,就是表达式括号嵌套层数过多时,我的程序会出现运行时间过长的TLE问题。在构造表达式因子时,参数作为一个表达式,对其进行拆解还需要经过表达式→项→因子三层,当括号嵌套过多时,则会出现内存不够用而运行时间过长的情况。为了修改TLE的bug,首先应该在每一次解析表达式字符串之前,先判断最外层的括号是否可以去除,直接通过字符串操作将多余括号略去,减少无意义的嵌套。其次,我的程序在某些类(比如Term类)的toString()方法中,出现了多次调用子因子的toString()方法的情况,而作用仅仅是为了进行分支语句的判断,这使得程序进行了大量无意义的toString嵌套操作,严重拖垮了运行时间。改为在上层类的toString()方法中最多只调用一次子因子的toString()方法,减少嵌套层数。经过修复后,代码可在规定时间内正常运行。
二、互测策略
在互测中我主要采用的方法有以下几种:
-
阅读别人程序的代码,第一次作业时程序结构还较为简单,可快速浏览全部代码,之后随着作业逐渐变得复杂,阅读全部代码太过浪费时间也不切实际,经过观察bug通常出现在对于输入字符串的处理上和输出字符串的toString函数上,所以我就重点阅读这两部分的代码。事实上也确实在这两部分发现的bug数较多。
-
自己构造特殊数据组合,如:常数、空串、
---x,-x**+0,(x*x)*(x*x)*(x*x)*(x*x)*(x*x)等等。 -
在第三次作业中,测试多重嵌套数据,如:
(((((((((((((-x))))))))))))),-x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x))))))))))))))等。(说来惭愧,我就是这个问题,也测出了其他人的TLE问题) -
利用Python的xeger包自动生成数据,并编写自动测试脚本程序来测试代码。(发现bug的主要手段)
三、应用对象创建模式
在第二次和第三次作业中,我都运用了工厂模式,通过传入因子的字符串来创建不同类型的因子。在第2次作业中,带来的好处还不明显,但在第3次作业中,使用工厂模式构造因子大大地简化了项的解析方法,降低了代码的复杂度,并且使得程序结构和逻辑都更加清晰。
由于第三次作业中,各类因子的添加需要在同一个位置进行判断,它们又实现同一个Factor接口,所以非常适合应用工厂模式。在实际应用中,我使用的是一个简单工厂模式,通过工厂类中提供的函数进行构造。但是,这种朴素的实现方法等价于用if...else对所有因子类进行遍历匹配,当因子类类型增加时还需要对工厂类进行修改,不符合开闭原则。一个符合开闭原则的实现方式是利用反射机制,虽然稍显复杂但可扩展性得以增强。
下面这是我的第三次作业中的实现方式:
public static Factor createFactor(String factorStr) throws Exception {
String str = factorStr;
Pattern sinp = Pattern.compile(sinFactor);
Pattern cosp = Pattern.compile(cosFactor);
Matcher sinm = sinp.matcher(str);
Matcher cosm = cosp.matcher(str);
if (str.matches(constFactor)) {
......
return new ConstFactor(str);
}
else if (str.matches(powFactor)) {
......
return new PowFactor(index);
}
else if (sinm.matches()) {
......
return new SinFactor(index, base);
}
else if (cosm.matches()) {
......
return new CosFactor(index, base);
}
else if (str.matches(polyFactor)) {
String polystr = str.substring(1, str.length() - 1);
return new PolyFactor(polystr);
}
else { throw new Exception("抛出异常"); }
}
}
四、对比和心得体会
经过和优秀代码的对比以及自己的反思,我觉得自己的程序还有以下几点值得改进:
- 对类进行分包。我的作业中把所有的代码都放在了src文件夹下,没有将类进行分包,这样对于类的数量较少的小型作业来说影响不大,但对于一些大型的工程项目,就要在对类分类的基础上进行分包,让代码组织更加高效合理。
- 程序架构还存在不合理的地方。有一些相对独立的功能可以独自拆分出一个类,使代码更简洁清晰。比如输入字符串的预处理,我是在Main类中直接进行的,可以提供专门进行字符串预处理的类,这样程序的组织架构将会更加合理清晰。
- 对未来设计留下的扩展性不足。第二次作业和第三次作业,我都在前一次作业的基础上进行了重构,这说明我的代码的可扩展性不强,以后写代码时一定要注意程序的功能扩展性,不能只顾解决眼前问题。所谓重构一时爽,
一直重构一直爽,呸,构错火葬场! - 关于正确性与性能。这次作业对我来说一个最大的教训就是,不能只考虑程序的正确性,却忽略了内存限制和运行时间限制。在将来思考代码结构时,不能把内存看作是一种无限的资源,而是要尽可能在保证正确性的情况下减小内存占用,并且要尽可能减少无意义的嵌套操作,满足运行时间限制。
- 仍然残留一些面向过程编码的风格习惯。写代码时仍然经常出现一些多重if...else嵌套的情况,导致复杂度难以降低。今后还需要大量的练习来适应面向对象的思想和风格。
- 第一单元的学习到此告一段落,今后还要更加努力!没有对象,就面向对象!