概述
第一单元的三次表达式求导作业,其实是面向对象 的一次比较系统的入门试炼。从作业想要我们达到的要求来说,从第一次作业我们就应该尝试开始搭建面向对象的整体架构,将表达式、项作为类,通过继承得到具体的项。事实上,在讨论区中,也能看到很多同学在第一次作业中就尝试构建出了合适的体系。而事先搭建了比较好的架构的前提下,后两次作业,则很明显是在第一次作业基础上的扩充:引入因子&加入三角函数类因子、加入嵌入处理和递归求导。
然而,从我自己的作业上来看,前两次针对第三次作业在面向对象上的铺垫是微乎其微的。这一方面源于在最开始还在努力适应java语言,同时自己针对面向对象的作用认识还不够深刻;另一方面,我对代码编写没有一个整体的工程化认识,对下一次作业可能出现的状况没有任何预判,编写时只关注于该次作业本身的任务上,导致代码毫无扩展性。可以说,在第三次作业中,我才真正地开始了面向对象编程,代码上有了显著变化。
下面我将逐次分析三次作业的作业要点、程序结构、出现的bug和互测策略。
第一次作业
第一次作业要求实现的是简单表达式的求导,因子只包含x幂次一类。又由于今年课程组在任务设计上取消了第一次作业的格式错误判断,所以在任务实现上十分单纯。
正是由于任务简单,加上如在概述中所说未对未来情况有任何预判,我的第一次作业是彻头彻尾的面向过程编程,一个多项式类,140行,一条路走到黑。
作业要点
- 正则表达式中捕获组与非捕获组的使用。
- 在储存表达式时,使用了Hash Map。在逐一读取表达式因子时,可以直接进行同项内的因子合并成为Hash Map中的一项,快速实现输出化简。
程序结构
由于采取了一个类走到黑的面向过程编程,以下只展示代码度量。(各参数含义见后:代码度量工具说明)
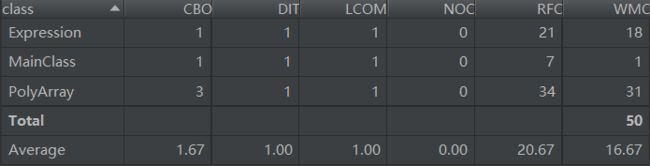
- 类度量:
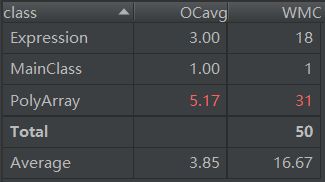
- 类复杂度度量:
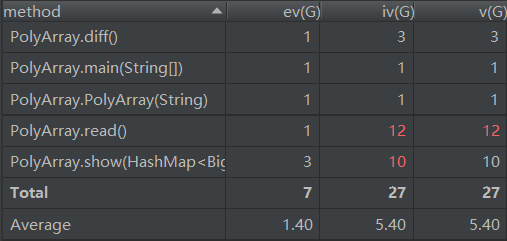
- 方法复杂度度量:
事实上,由于只有一个类,可以说几乎没有所谓高内聚低耦合的运用;复杂度方面,整个类的循环复杂度很高。同时,由于将表达式输入、识别全部放在read函数中,其方法的设计复杂度和结构复杂度都相当高。这次代码出去完成了应有的任务,在其结构上可以说除了思路简单,是一无是处的。
出现的bug&互测策略
由于任务简单以及在代码架构上实现的比较无脑,在强测中没有出现任何问题。但在互测环节,我被hack了14次;所幸,hack点全部集中在我画蛇添足加的一个错误的WRONG FORMAT!判定上。在删去之后,即全部解决。
互测策略上,我在一开始采用了讨论课上同学提示的对拍。然而,使用时发现,由于测试点随机生成,并不十分有效。于是,我的互测策略主要是自行构建较易出错的数据点以及通过阅读代码发现问题,并逐一手动测试。这样虽然效率也比较低,但在实操过程确实通过阅读其他同学的代码对自己的代码进行了反思,也在互测结果出来之前意识到了自己的bug;这也算是有效吧。
第二次作业
本次任务加入了三角函数类因子,制造了不同类别因子储存和乘法求导上面的障碍。
在本次作业中,我尝试将表达式类与项类从Main Class中区分出来,分别拥有一些属性;然而,具体的因子区分仍停留在函数层面。
作业要点
- 在具体储存时,仍然利用Hash Map,每个表达式中的项为Hash Map中的一项,于是Hash Map中的key成为一个包含三个Big Integer的数组(分别是x,sin(x),cos(x) 的幂指数),而Hash Map的value这是每项合并过后的常数因子。这样做的好处是在每一项求导时只用依照相同的格式进行展开,实现十分简单;缺点也显而易见,代码毫无扩展性。于是第三次加入嵌套之后,我进行了十分彻底的代码重构。/糟心
- 本次作业我认为实现上比较好的是利用正则表达式单独进行的表达式的拆分:通过识别+(实现对减号情况进行处理)拆分项、通过识别*拆分因子。这样做使我的表达式一开始就拥有了项的Array List、项拥有因子的Array List,使后续处理变的十分容易。(在第三次作业中我仍然沿用该拆分方法,但由于格式处理变得复杂,给自己制造了一些困难。)
程序结构
- 类度量:
- 类复杂度度量:
- 方法复杂度度量:
由于加入了表达式类和项类,复杂度上有了一些改善。由于输入处理、存储集中在Poly Array 类中,其平均循环复杂度高是必然的,解决方法就只有重构。match Term方法设计复杂度较高的原因还是由于将全部表达式识别集中于该方法。
出现的bug&互测策略
由于互测之中没有WRONG FORMAT!判断,我在互测过程中没有被发现任何bug。而在强测中出现了由于对space解读偏差,以及对\s概念的认知偏差,导致中测一个点格式错误。
互测策略上,由于第一次作业中效率较低,我在本次作业搭建时就有意识的记录所有易出现问题的数据点,并以此为基础对同组同学的代码进行有针对性的测试,hack到了5个点,算是有些进步。
第三次作业
本次任务主要加入表达式因子的组合嵌套。由于识别嵌套、递归复合求导上的实现困难,相较于前两次作业来说,第三次作业难度陡然加大。
难度的上升同时意味着需要有一个较为完善的代码架构才能比较容易的实现任务。(对我而言等于重构)于是,喜闻乐见,我在本次作业中终于开始了真正的面向对象编程。
作业要点
- 面向对象特点:构建了继承自因子类的三角函数类、常数类、x幂次类、表达式类,每个子类实现自己的求导方法,对因子父类的求导方法进行覆盖。
- WRONG FORMAT判定
- 输出化简!!!:这在本次作业中给我制造了最多的困难。由于我采用的主要是得到输出后化简的策略(表达式类输出会继续参与递归),在化简时重新用正则表达式读输出。在考虑不充分的情况下,导致很多化简情况考虑有偏差,影响结果的正确性,带来很多不必要的麻烦。
程序结构
在表达式类、因子类及其各个子类之外,我还构建了输出类,其与表达式类的结果交互,处理输出。各类关系如图所示。
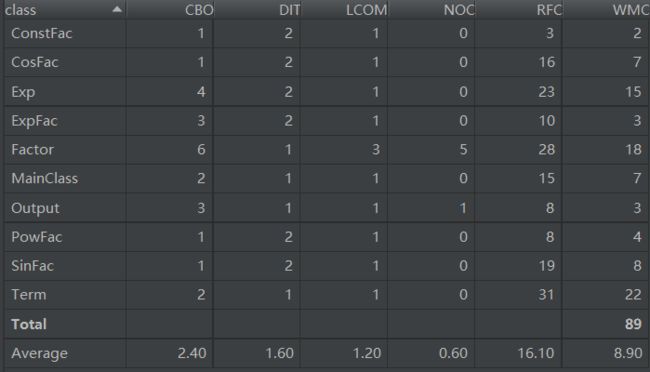
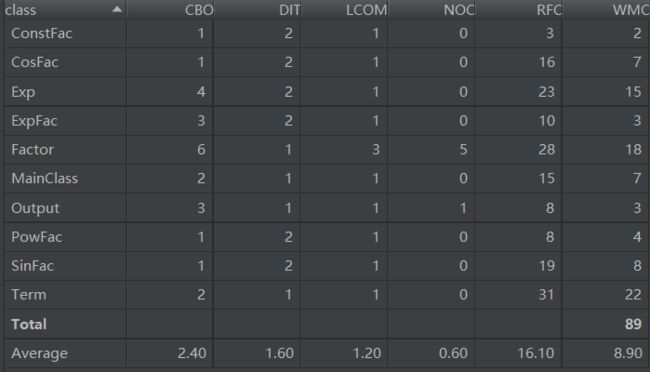
- 类度量:
- 类复杂度:
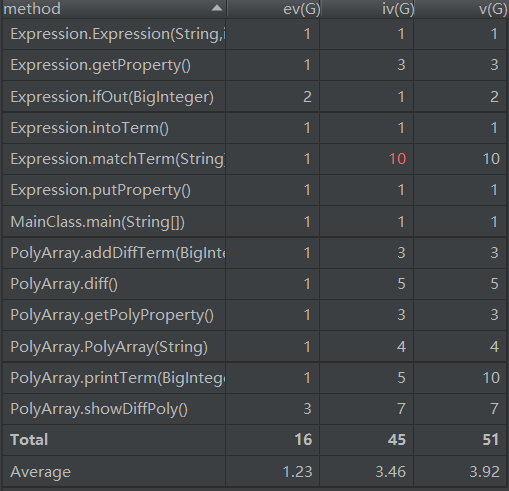
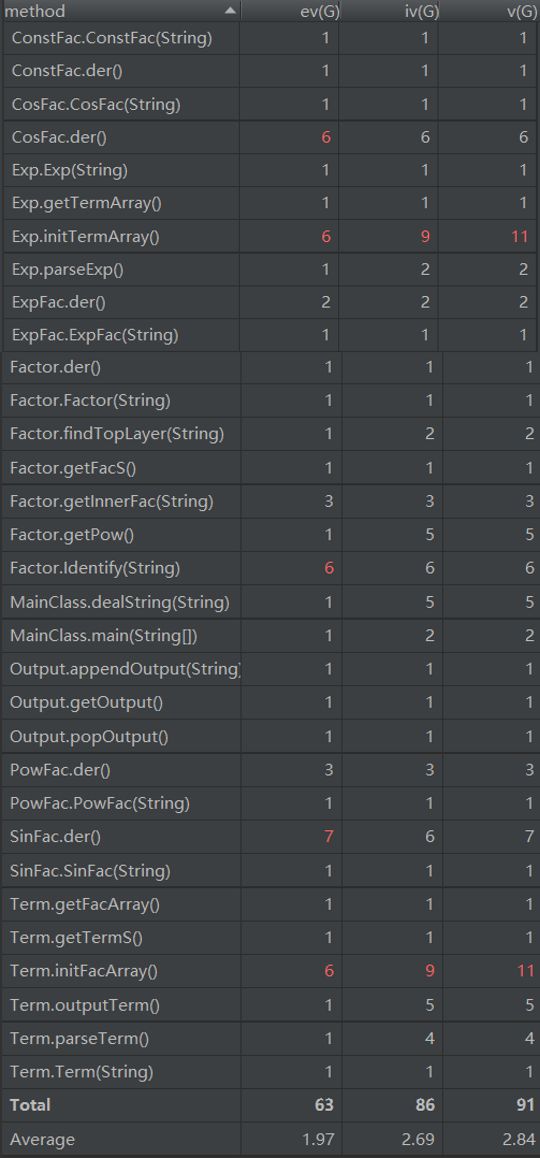
- 方法复杂度:
整体来看,第三次的代码在内聚上有了一些显著进步,不管是类复杂度还是方法复杂度均低于前一次作业,说明抽象层次的运用确实在一定程度提高了程序的“高内聚,低耦合”程度。
几个平均循环复杂度较高的类在递归下降方法的实现过程中可以进一步抽取逻辑降低复杂度,并且在解析-生成实例过程可以运用设计模式--工厂模式,以进一步降低类间耦合度。
出现的bug&互测策略
强测的问题主要集中在如上文所说的输出化简,包括针对0*、1*、常数项、冗余括号的化简。事实上,我所尝试的化简都十分初级,并未涉及到诸如表达式合并、拆括号等更有效的化简,对结果性能影响其实并不大;但却严重的阻碍了结果的正确性。bug修复环节,主要采用删去自己所有错误化简的方式,效果卓越(\傻眼)。
本次由于个人身体状况原因,在周六才恢复并开始写代码;同时也因为莫名其妙的输出化简耽搁了时间,导致最终一个中测点未能通过(也是因为化简原因),未进入互测。十分遗憾,下次再战。
总结
整体上来看,三次作业我的在代码上的改善是十分明显的,也终于拥有了面向对象编程的基本感觉。反思起来,三次作业其实就是逐渐加深面向对象编程思维的过程,重点在思维转换上,总体任务量不算很大,第三次作业比较繁琐且我的实现不够简洁的情况下也不过440行左右。
在做整个单元作业及阅读其他同学优秀代码的过程中,我有如下反思:
- 对于接口的运用还不够熟练
- 应该尝试工厂类等更为系统的的工程方法
- 第三次作业化简上有较多遗憾(部分是因为身体原因导致),没有在这方面进行有效的锻炼
以下是我参考相应书籍和网站资料,对在本单元作业中可以进行的设计模式进行的思考拓展。
关于设计模式的思考
- 设计模式原则--总原则:开闭原则
开闭原则就是说对扩展开放,对修改关闭。在程序需要进行拓展的时候,不能去修改原有的代码,而是要扩展原有代码。即是为了使程序的扩展性好,易于维护和升级。
-
- 单一职责原则
-
- 里氏替换原则
-
- 依赖倒转原则
-
- 接口隔离原则
-
- 迪米特原则(最少知道原则)
-
- 合成复用原则
- 设计模式初步--创建模式
-
- 下面列出了基本的创建模式。
-
- 简单工厂模式
-
- 工厂方法模式
-
- 抽象工厂模式
-
- 单例模式
-
- 建造者模式
-
- 原型模式
后续作业难度显然会进一步加大。针对多线程等即将面临的挑战,希望自己能在反思的基础上进一步提升,也希望自己能挺住(同时指身体和思维层面)。加油。
代码度量工具说明
- 使用工具
- IDEA 插件:Metric Reloaded
- 两类分析工具说明
- Chidamber-Kemerer metrics
- CBO: 类间耦合度
- Chidamber-Kemerer metrics
-
-
- DIT: 继承树深度
-
-
-
- LCOM: 类内聚度
-
-
-
- RFC:类响应度
-
Complexity metrics
-
- Class metrics
-
-
- OCavg : 类方法的平均循环复杂度
-
-
-
- WMC:类方法权重(可理解为方法数量等)
-
-
- Method metrics
-
-
- ev(G): 基本复杂度
-
-
-
- iv(G): 模块设计复杂度
-
-
-
- v(G): 模块判定结构复杂度
-