JAVA数据结构代码
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。
常用结构:数组、栈、队列、链表、树、图、堆、散列表
代码文件下载地址:JAVA数据结构代码
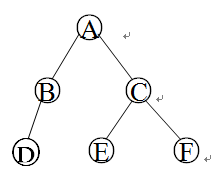
用链式存储结构表示以下的一棵树,并用前序、中序或后序算法输出该树的结点。
public class BinTree { // 二叉树类
private BinTreeNode root;
BinTree() { // 构造方法
root = null;
}
BinTree(Object item, BinTree left, BinTree right) { // 构造方法
BinTreeNode l = null, r = null;
if (left == null)
l = null;
else
l = left.root;
if (right == null)
r = null;
else
r = right.root;
root = new BinTreeNode(item, l, r);
}
public boolean root(Object x) { // 返回根结点元素函数
if (root != null) {
x = root.getData();
return true;
} else
return false;
}
public void MakeTree(Object x, BinTree left, BinTree right) { // 创建二叉树
if (root != null || left == right)
return;
root = new BinTreeNode(x, left.root, right.root);
left.root = null;
right.root = null;
}
public void BreakTree(Object x, BinTree left, BinTree right) { // 删除二叉树
if (root == null || left == right || left.root != null
|| right.root != null)
return;
x = root.getData();
left.root = root.getLeft();
right.root = root.getLeft();
// delete root;
root = null;
}
public static void PreOrder(BinTreeNode r, Visit vs) {// 前序遍历二叉树
if (r != null) {
vs.print(r.data);
PreOrder(r.getLeft(), vs);
PreOrder(r.getRight(), vs);
}
}
public static void InOrder(BinTreeNode r, Visit vs) {// 中序遍历二叉树
if (r != null) {
InOrder(r.getLeft(), vs);
vs.print(r.data);
InOrder(r.getRight(), vs);
}
}
public static void PostOrder(BinTreeNode r, Visit vs) { // 后序遍历二叉树
if (r != null) {
PostOrder(r.getLeft(), vs);
PostOrder(r.getRight(), vs);
vs.print(r.data);
}
}
public static void LevelOrder(BinTreeNode r, Visit vs) // 层次遍历二叉树
throws Exception {
java.util.Queue
if (r == null)
return;
BinTreeNode current;
q.add(r);
while (!q.isEmpty()) {
current = (BinTreeNode) q.remove();
vs.print(current.data);
if (current.getLeft() != null)
q.add(current.getLeft());
if (current.getRight() != null)
q.add(current.getRight());
}
}
}
public class BinTreeNode { // 二叉树结点类
private BinTreeNode lChild; // 左孩子结点对象引用
private BinTreeNode rChild; // 右孩子结点对象引用
public Object data; // 数据元素
BinTreeNode() { // 构造二叉树结点
lChild = null;
rChild = null;
}
BinTreeNode(Object item, BinTreeNode left, BinTreeNode right) { // 构造二叉树结点
data = item;
lChild = left;
rChild = right;
}
BinTreeNode(Object item) { // 构造二叉树结点
data = item;
lChild = null;
rChild = null;
}
public BinTreeNode getLeft() { // 返回左孩子
return lChild;
}
public BinTreeNode getRight() { // 返回右孩子
return rChild;
}
public Object getData() { // 返回数据元素
return data;
}
public void setLeft(BinTreeNode left) { // 设置左孩子
lChild = left;
}
public void setRight(BinTreeNode right) { // 设置右孩子
rChild = right;
}
}
public class Visit { //输出显示类
public void print(Object item) {
System.out.print(item + " ");
}
public static void main(String args[]) throws Exception {
BinTreeNode D = new BinTreeNode("D", null, null);
BinTreeNode B = new BinTreeNode("B", D, null);
BinTreeNode E = new BinTreeNode("E", null, null);
BinTreeNode F = new BinTreeNode("F", null, null);
BinTreeNode C = new BinTreeNode("C", E, F);
BinTreeNode A = new BinTreeNode("A", B, C);
Visit vs = new Visit();
System.out.print("前序遍历:");
BinTree.PreOrder(A, vs);
System.out.println();
System.out.print("中序遍历:");
BinTree.InOrder(A, vs);
System.out.println();
System.out.print("后序遍历:");
BinTree.PostOrder(A, vs);
System.out.println();
System.out.print("层次遍历:");
BinTree.LevelOrder(A, vs);
}
}