OO第一单元总结

BUAA_OO 第一单元表达式求导作业总结

一、    作业总结

这三次作业是关于表达式求导的一个层递式project。在通过pre初步了解了面向对象的思想之后的一次实践。以下是针对三次作业不同设计思路的总结。

第一次作业：

实现方法：

第一次作业是对一些简单的表达式进行求导。此次的表达式中只包含一些幂函数和常数进行相加减。由于是第一次作业，其对设计思路的要求不是很高，当时在做的时候重点放在了表达式的解析过程之上，即如何利用正则表达式来判断一个表达式的合法性并从合法的表达式中提取出各个项。对于这三次的作业，我都是按照设定的形式化表述来进行正则表达式的构造的。我首先从最底层的一些表述进行正则表达式的构造，再通过已经构造好了的表述进行迭代来完成对更高一层的表述的构造。这次作业中我是以项为基础进行了表达式的拆分。我设计了一个Poly类来表示项，这个类有两个参数coef来表示系数和index来表示指数。如果将常数看成指数为0的幂函数，那么全部的项和其求导后的结果则都可以由Poly类来描述。而另一个难点是针对表达式求导的结果进行化简。在这次作业中，我使用了HashMap来进行化简问题。其中，将求导后得到的项的指数作为key，将项作为value存放在HashMap中。在计算出新的项后，如果存在其key值，则将两个Poly类合并，即完成同类项合并。否则将新的键值对放入HashMap。最后是针对“+”的化简。因为此次的处理是将所有的“+”、“-”运算符放在了Poly类中，故如果第一项系数为正，则可以少输出一个“+”。我采取的方式为重写一个HashMap，将原有的HashMap按Poly类的系数按降序排列，如果这样得到的结果是以“+”开头则不将“+”输出来达到优化的目的。

 

代码度量：

ev(G)表示一个方法的结构化程度。

Iv(G)为表示一个方法和他所调用的其他方法的紧密程度。

v(G)为循环复杂度。

OCavg为平均循环复杂度。

WMC为总循环复杂度。

我这三次的作业在这个方面做的都不好，尤其是第三次作业各个类的平均循环复杂度很高。在以后写代码之前一定要注意这个方面。

 

 

 

 

 

 

 

第二次作业

实现方法：

第二次作业相较于第一次作业加入了三角函数sin(x)和cos(x)。由于此次作业没有加入嵌套，每一项只是多个函数相乘所得到的，所以我们可以用系数、sin(x)指数、cos(x)指数和x指数来确定一个项。此次化简我仍延续上一次的思路利用HashMap的方式来化简。为了便于合并同类项，我设计了一个HashKey的类用来保存sin(x)指数、cos(x)指数和x指数同时能够作为HashMap的key，而将其对应的系数作为HashMap的value，这样就能便于合并同类项。而针对此次作业，我将重点放在了三角函数的化简之上，多是利用sin(x)^2+cos(x)^2=1等式来进行化简。我通过遍历HashMap，对一个项，如果存在另一个项两者的系数互为相反数且其sin或cos的指数相差2，其余指数相等则两者就可以合并。

 

代码度量：

 

 

 

 

 

 

 

 

第三次作业

实现方法：

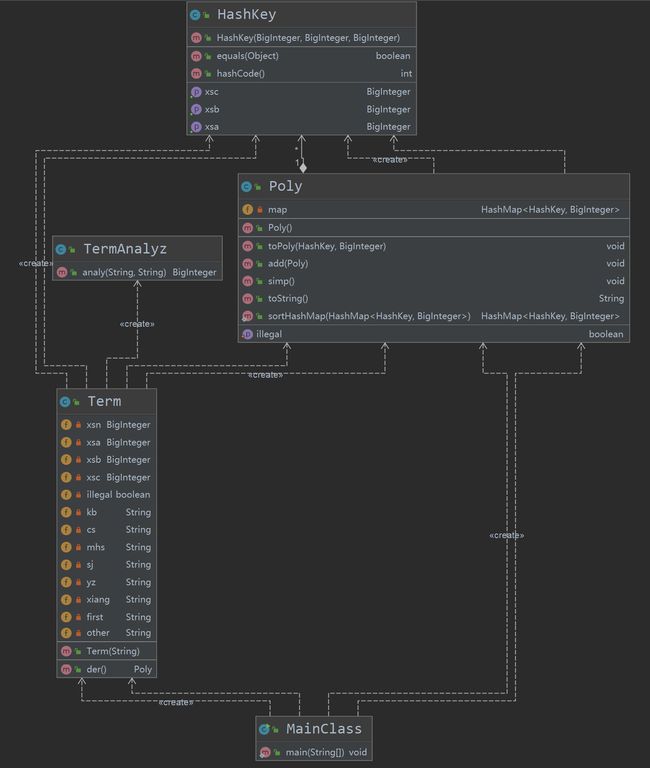
第三次作业在前两次的作业基础上加入了复合函数求导，这个改变让整个题目变得复杂起来。首先是在表达式的解析之上，因为出现了表达式因子这个特殊的因子，所以表达式也出现了递归定义。而java中的正则表达式之中是不能通过递归来定义的，所以这个就需要通过其他的方法来进行表达式的解析。而表达式因子带来的另一个问题是括号匹配的问题，这将会出现括号中嵌套有括号的情况出现。针对这情况，我采用了指导书中的方法，对运算建立了加减法类、乘法类和嵌套类，而对函数则建立了对应的常数类、幂函数类和三角函数类。而针对表达式则建立了表达式类、项类和因子类，并建立对应的mattch方法来进行合法性检查和build方法来进行表达式的构造。在处理表达式的开始就先进行括号匹配，我选择将三角函数的括号都替换成“[ ”、“]”，而将表达式因子的括号替换成“{”、“}”，这样就能通过对应的正则表达式来完成表达式的解析。而由于嵌套的存在，之前的求导方法就不能再使用了。这一次我采用了树形结构来进行表达式的存储。但是这样的弊端就是在化简上很是困难，由于这个的输出类型都是String，所以这一次我就只化简了“1*”、“**1”和“0”，所以性能分就有许多没有得到。

 

代码度量：

 

 

 

 

 

 

 

 

 

 

二、bug分析

强测

第一次作业强测中我没有出现bug。第二次作业的强测出现了一个关于空白符的问题。这个问题在第一次作业中就有提及，但是由于第一次的强测点没有涉及这个方面，故在第二次作业才发现这个问题。究其根本还是对正则表达式的理解不够深入，其中\\s是匹配的所有空白符，而题目的描述则是只能出现空白符和制表符。针对这个情况，我们可以通过其ASCII码来进行判断，而如果要用正则表达式的话则可用“ (space)|\\t”来进行表述。在第三次作业中则出现了对于表达式括号的替换出现了错误，只对“*”后的括号进行了替换，而忽视了对“+”和“-”后的表达式因子的括号进行替换所以出现了问题。这个同质bug在互测中也出现了多次。由此可见在对表达式进行解析的时候也得十分细致。

互测

由于是第一次接触互测这种模式，我对此没有太多经验。在这三次互测之中，有人通过脚本来寻找bug，有人则用一些易出现问题的数据进行测试。而我选择在自己写代码的时候将自己出现bug的数据记录下来用来寻找其他人的bug。而这样的销量不是很高，在之后的作业之中在这个方面可以多下功夫。

三、创建模式分析

这一次作业的主题是表达式求导。由于表达式的形式不断的复杂，求导的法则也更加的多样。最终我采取的是二叉树的结构来进行表达式的解析。此前也有提到一些关于类的创建，我此次的表达式树是通过计算类和函数类来构造的。这两个类中我对其分别实现了相应的输出方法和求导方法。而对每一个计算类都有两个子节点，这个子节点可以是计算类，也可以是函数类。而函数类则没有子节点，可以直接通过求导来进行运算。而在这一次作业中，我在互测中被hack了一个这个结构方面的bug，那就是多个幂函数相乘导致的嵌套次数太多而CPU运算超时的问题。后来我针对这个模式对其进行了改进，这接将两个幂函数相乘合并后返回一个幂函数类来化简，这样就能有有效的节省CPU运行的时间了。

四、心得体会

这三次作业虽然是层递式的作业，但是我每一次作业都要对上一次的作业来进行重构。从这一点看来，我对OO代码的这个可迭代性上做到不好，在进行一次作业时仅仅是将目标定在了这一次的任务而没有进行长远的考量。之后在做作业的时候一定要注意这个方面。再者就是关于代码度量方面的，在完成一次作业前，一定要先完成对其的构思，多多注意耦合度方面的问题。最后是关于互测方面，互测不仅仅是找bug的过程，其还能学习到别人许多优秀的代码。面对这些优秀的代码，我要学会从中学习，进一步体会面向对象的思维。