HW1
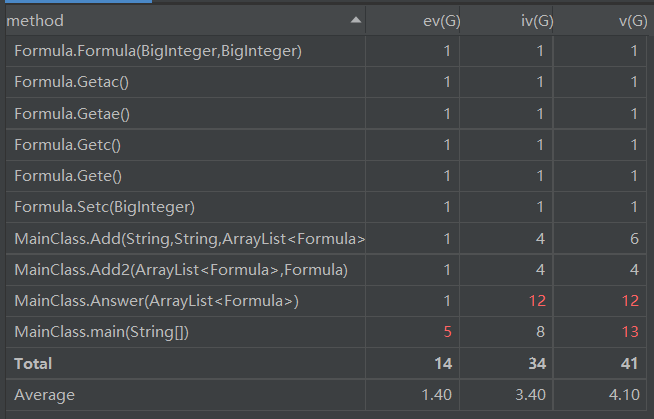
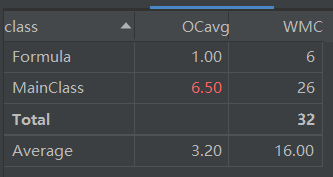
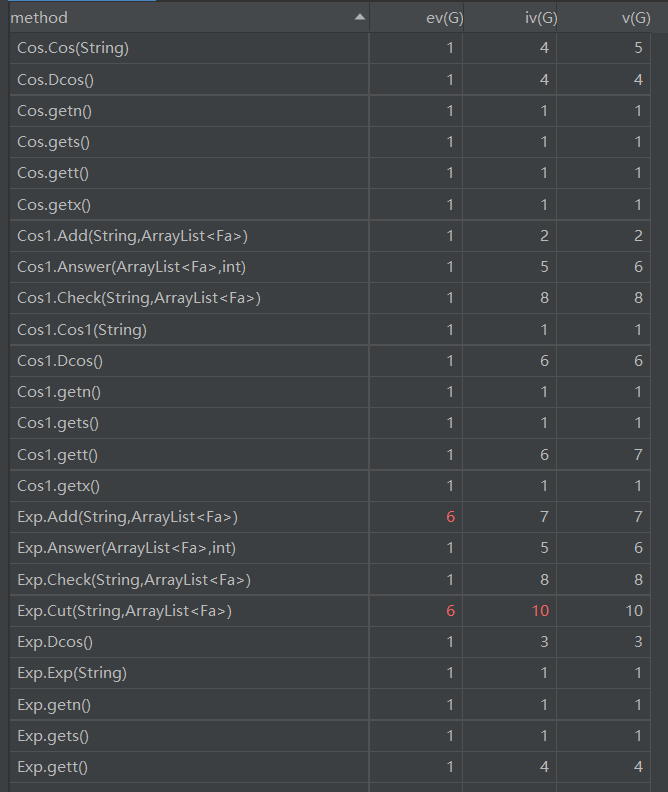
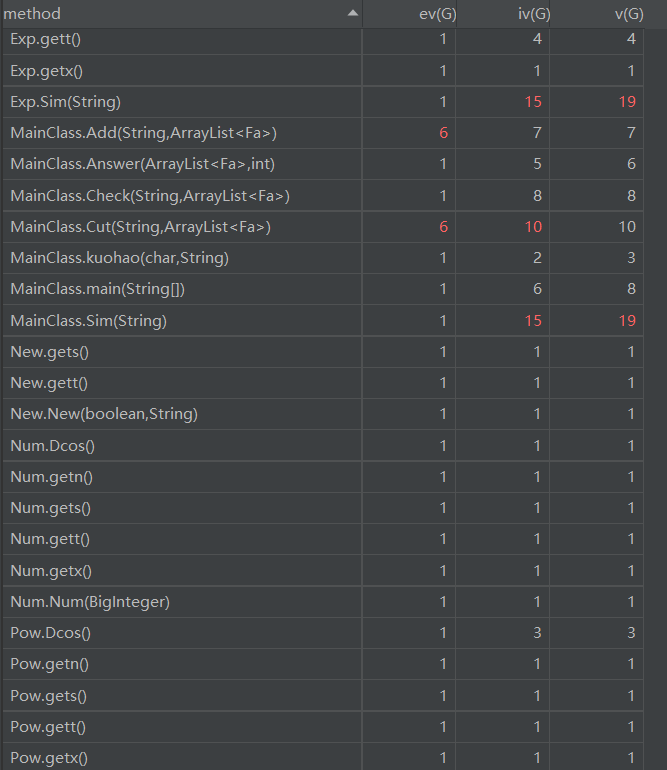
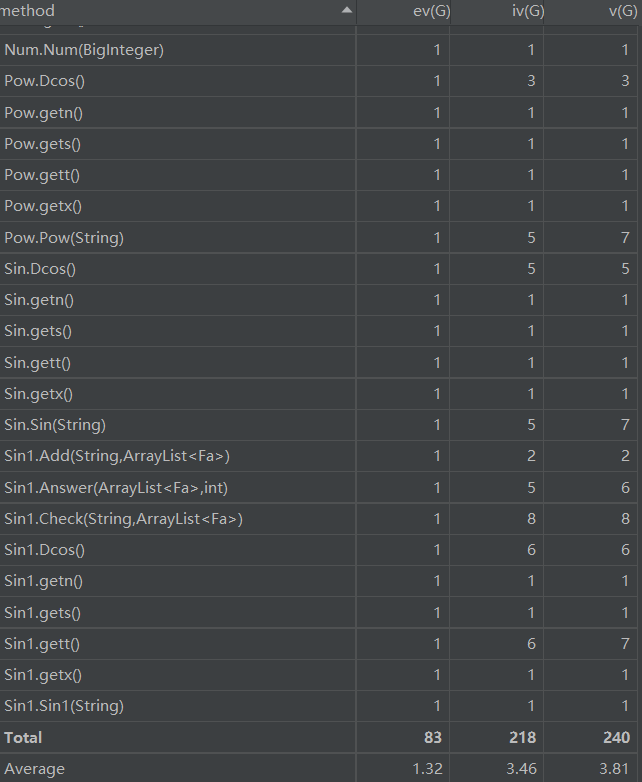
复杂度分析
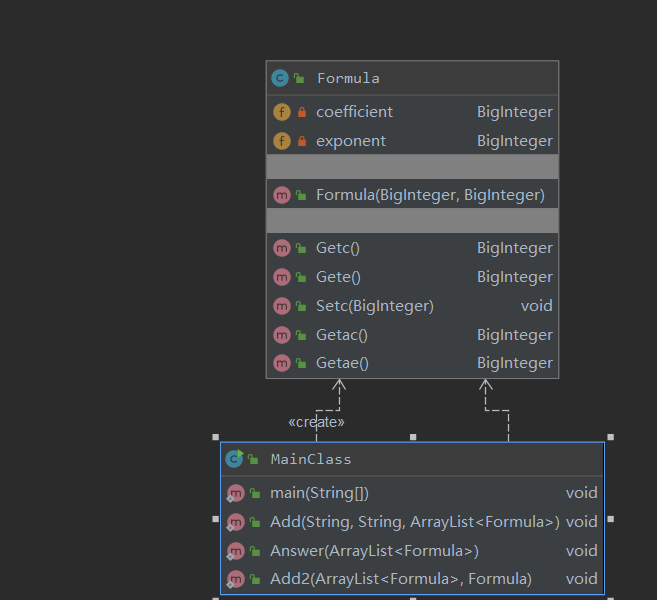
UML图
思路简介
在第一次作业中由于没有考虑格式错误,所以可以首先删去空白字符,然后将连续出现的加减号化简为一个运算符号(如+-化简为-)然后根据+-号对处理后的表达式进行分割,分割后装入Formula类中(格式为a*x**b)就可以轻松通过基本求导规则得出导数,然后将求导后系数为0的删去,指数为0的去除“*x**b”然后再进行输出。
结构分析
在第一次作业中值建立了一个类,用来存储幂函数,而在main中使用了大量方法来完成对表达式的处理和输出答案,这也就导致Main里行数特别多,而用来存储幂函数的类就比较简单,面向对象性体现的不充分。
HW2
复杂度分析
UML图
思路简介
在第二次作业中增添了sin和cos函数以及表达式错误的判断,由于本次作业并未在空格上做文章,所以还是可以先删去空格,然后使用正则表达式来判断输入的表达式格式是否错误,
然后扩展了上一次的Formula类(变为a*x**b*sin(x)**c*cos(x)**d)还是通过加减号配合正则表达式对原有表达式进行分割,然后用“*”来对处理后得到项进行分割并存入,求导过程与上一次类似。
结构分析
第二次作业是在第一次作业基础上完成的,为了解决幂函数次数的限制在解析时需要返回boolean变量所以新建了一个类来完成返回变量和字符串的工作。
HW3
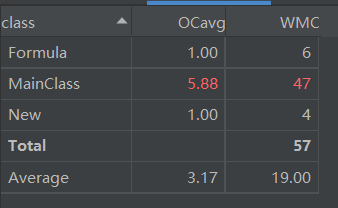
复杂度分析
UML
思路简介
首先判断空格的位置是否存在错误然后将空格删去,再判断表达式是否有错误然后新建了sin1(sin括号中为嵌套)之类的类并进行分割求导,嵌套类会去除外部的括号在分析其内部的表达式。
结构分析
第三次作业由于嵌套的出现导致前两次作业的的经验几乎不可借鉴,只能进行大范围的重构,在结构分布上非常复杂,首先设立了一个接口,然后有设立了sin、sin1、pow等类来实现这个接口,部分嵌套类中还需要像面中一样再次解析表达式。
BUG分析
在第一单元的学习中,主要BUG集中在第三次作业,其中最为严重的BUG就是对因子截取幂指数时直接对类中存储的表达式进行了剪切,导致了之后在想调用类中未进行求导的表达式时互发生错误,其次在考虑空格位置错误时漏掉了cos( - 1)这样的错误。第一次作业的BUG出现在调用对象时字母打错,第二次则未发现BUG。
寻找BUG策略
在寻找BUG主要是靠自行构造一些边界数据,或者根据对方的代码来有针对性的找出BUG(效率偏低),也有时候能通过对方的输出模式来推测对方输出时可能会出现什么问题来构造数据。
应用对象创建模式个人感觉
第一次和第二次主要就是建立了一个因子类。
第三次作业中使用了接口和工厂化方法,将可能出现的因子类型都建立了一个类,用接口来统一管理这些类。
心得与体会
在第一单元的学习主要的问题还是体现在“面对对象”体现的不够充分第一次和第二次作业更多的是像“面向过程”,第三次作业虽然使用了接口和工厂模式,但是逻辑和结构比较混乱导致BUG比较多,而且在自己DEBUG时很多情况都没有考虑到,有些特殊情况虽然考虑到了但是由于输出过于复杂没有细看导致没能成功发现BUG。个人感觉第一单元的三次作业难度提升的速度很大导致每次都要相当大面积的重构代码(我自己程序的可扩展性不够也是很重要的原因),在设计类上很多地方显得冗余,大量使用static方法这种“面向过程”的做法,导致感觉每次作业代码结构也显得很混乱。