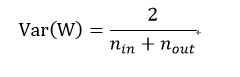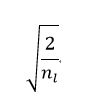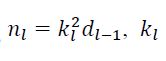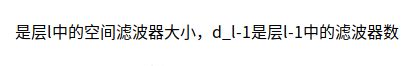权重初始化方法及适用情况

1. Gaussian

从具有固定均值（例如0）和固定2的标准差（例如0。01）的搞死分布中随机抽取权重，这是最常用的.

一般使用截断高斯。

2. Xavier

这种方法是但的缩放均值或者搞死分布进行初始化

在caffe,他通过从零均值和特定方差的分布中绘制他们来初始化网络中的权重。

其中w是所有讨论的神经元的初始化分布，而n_in是摄入神经元的神经元的数量，使用的分布通常是高斯均匀分布。

                                                  

其中n_out是结果被亏送到神经元的结果。

Reference:

[1] X. Glorot and Y. Bengio. Understanding the difficulty of training deepfeedforward neural networks. In International Conference on Artificial Intelligence and Statistics, pages 249–256, 2010.

[2] Y. Jia, E. Shelhamer, J. Donahue, S. Karayev, J. Long, R. Girshick, S.Guadarrama, and T. Darrell. Caffe: Convolutional architecture for fast featureembedding. arXiv:1408.5093, 2014.

3. MSRA

                                                  

Reference:
[1] Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification, Technical report, arXiv, Feb. 2015

4 .把权重初始化为0

把权重初始化为0的方式不可取的。 这是因为如果把w初始化0，那么每一层的神经元学到的东西都是一样的（输出是一样的），而且在反向传播的时候，他们的梯度相同。在这种情况下， 隐含层单元就会完全一样，因此他们完全对称。导致模型性能下降，还会出现梯度消失的情况。

5. 小随机数初始化

只要随机初始化W你就有不同的隐含单元计算不同的东西，因此打破对称性。 我们通常倾向于初始化为很小的随机数。因为如果你用tanh或者sigmoid激活函数，当 W很大，激活函数的输出值就会很大或者很小，因此这种情况下你很可能停在tanh/sigmoid函数的平坦的地方， 这些地方梯度很小也就意味着梯度下降会很慢，因此学习也就很慢。

.Xavier初始化（tanh）

尽可能的让输入和输出服从相同的分布，这样就能够避免后面层的激活函数的输出值趋向于0。 让信息可以在网络中均匀的分布一下。 输出值在很多层之后依然保持着良好的分布，有利于优化神经网络

权重分布：均值为0，方差为1 / n（输入的个数 ）的 均匀分布

 

缺点：对非线性函数不具有普适性

深度学习中神经网络的几种权重初始化方法

2018年04月25日 15:01:32 天泽28 阅读数 9225

版权声明：本文为博主原创文章，转载或者引用请务必注明作者和出处，尊重原创，谢谢合作 https://blog.csdn.net/u012328159/article/details/80025785

 

深度学习中神经网络的几种权重初始化方法

       在深度学习中，神经网络的权重初始化方法对（weight initialization）对模型的收敛速度和性能有着至关重要的影响。说白了，神经网络其实就是对权重参数w的不停迭代更新，以期达到较好的性能。在深度神经网络中，随着层数的增多，我们在梯度下降的过程中，极易出现梯度消失或者梯度爆炸。因此，对权重w的初始化则显得至关重要，一个好的权重初始化虽然不能完全解决梯度消失和梯度爆炸的问题，但是对于处理这两个问题是有很大的帮助的，并且十分有利于模型性能和收敛速度。在这篇博客中，我们主要讨论四种权重初始化方法：

• 把w初始化为0
• 对w随机初始化
• Xavier initialization
• He initialization

1.把w初始化为0
我们在线性回归，logistics回归的时候，基本上都是把参数初始化为0，我们的模型也能够很好的工作。然后在神经网络中，把w初始化为0是不可以的。这是因为如果把w初始化0，那么每一层的神经元学到的东西都是一样的（输出是一样的），而且在bp的时候，每一层内的神经元也是相同的，因为他们的gradient相同。下面用一段代码来演示，当把w初始化为0：

def initialize_parameters_zeros(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    parameters = {}
    np.random.seed(3)
    L = len(layers_dims)  # number of layers in the network
    for l in range(1, L):
        parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l - 1]))
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
    return parameters

我们可以看看cost function是如何变化的：

能够看到代价函数降到0.64（迭代1000次）后，再迭代已经不起什么作用了。

2.对w随机初始化
目前常用的就是随机初始化，即W随机初始化。随机初始化的代码如下：

 

def initialize_parameters_random(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.
    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    np.random.seed(3)  # This seed makes sure your "random" numbers will be the as ours
    parameters = {}
    L = len(layers_dims)  # integer representing the number of layers
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1])*0.01
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
    return parameters

 

 

乘0.01是因为要把W随机初始化到一个相对较小的值，因为如果X很大的话，W又相对较大，会导致Z非常大，这样如果激活函数是sigmoid，就会导致sigmoid的输出值1或者0，然后会导致一系列问题（比如cost function计算的时候，log里是0，这样会有点麻烦）。随机初始化后，cost function随着迭代次数的变化示意图为：

能够看出，cost function的变化是比较正常的。但是随机初始化也有缺点，np.random.randn()其实是一个均值为0，方差为1的高斯分布中采样。当神经网络的层数增多时，会发现越往后面的层的激活函数（使用tanH）的输出值几乎都接近于0，如下图所示：

顺便把画分布的图的代码也贴出来吧：

 

import numpy as np
import matplotlib.pyplot as plt

def initialize_parameters(layer_dims):
    """
    :param layer_dims: list,每一层单元的个数（维度）
    :return:dictionary,存储参数w1,w2,...,wL,b1,...,bL
    """
    np.random.seed(3)
    L = len(layer_dims)#the number of layers in the network
    parameters = {}
    for l in range(1,L):
        parameters["W" + str(l)] = np.random.randn(layer_dims[l],layer_dims[l-1])*0.01
        parameters["b" + str(l)] = np.zeros((layer_dims[l],1))
    return parameters

def forward_propagation():
    data = np.random.randn(1000, 100000)
    # layer_sizes = [100 - 10 * i for i in range(0,5)]
    layer_sizes = [1000,800,500,300,200,100,10]
    num_layers = len(layer_sizes)
    parameters = initialize_parameters(layer_sizes)
    A = data
    for l in range(1,num_layers):
        A_pre = A
        W = parameters["W" + str(l)]
        b = parameters["b" + str(l)]
        z = np.dot(W,A_pre) + b #计算z = wx + b
        A = np.tanh(z)
        #画图
        plt.subplot(2,3,l)
        plt.hist(A.flatten(),facecolor='g')
        plt.xlim([-1,1])
        plt.yticks([])
    plt.show()

还记得我们在上一篇博客一步步手写神经网络中关于bp部分导数的推导吗？激活函数输出值接近于0会导致梯度非常接近于0，因此会导致梯度消失。
3.Xavier initialization
Xavier initialization是 Glorot 等人为了解决随机初始化的问题提出来的另一种初始化方法，他们的思想倒也简单，就是尽可能的让输入和输出服从相同的分布，这样就能够避免后面层的激活函数的输出值趋向于0。他们的初始化方法为：

def initialize_parameters_he(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.

    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    np.random.seed(3)
    parameters = {}
    L = len(layers_dims)  # integer representing the number of layers
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(1 / layers_dims[l - 1])
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
    return parameters

来看下Xavier initialization后每层的激活函数输出值的分布：

r

能够看出，深层的激活函数输出值还是非常漂亮的服从标准高斯分布。虽然Xavier initialization能够很好的 tanH 激活函数，但是对于目前神经网络中最常用的ReLU激活函数，还是无能能力，请看下图：

当达到5，6层后几乎又开始趋向于0，更深层的话很明显又会趋向于0。
4.He initialization
为了解决上面的问题，我们的何恺明大神（关于恺明大神的轶事有兴趣的可以八卦下，哈哈哈，蛮有意思的）提出了一种针对ReLU的初始化方法，一般称作 He initialization。初始化方式为：

 

def initialize_parameters_he(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.

    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    np.random.seed(3)
    parameters = {}
    L = len(layers_dims)  # integer representing the number of layers
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(2 / layers_dims[l - 1])
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
    return parameters

来看看经过He initialization后，当隐藏层使用ReLU时，激活函数的输出值的分布情况：

效果是比Xavier initialization好很多。现在神经网络中，隐藏层常使用ReLU，权重初始化常用He initialization这种方法。

 

关于深度学习中神经网络的几种初始化方法的对比就介绍这么多，现在深度学习中常用的隐藏层激活函数是ReLU，因此常用的初始化方法就是 He initialization。

以上所有代码都放到github上了，感兴趣的可以看一波：compare_initialization.




参考文献
1. Xavier Glorot et al., Understanding the Difficult of Training Deep Feedforward Neural Networks
2. Kaiming He et al., Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classfication
3. Andrew ng coursera 《deep learning》课
4. 夏飞 《聊一聊深度学习的weight initialization》