汉诺塔的非递归实现及其思考

汉诺塔问题的非递归实现及其思考

有关问题的递归实现和非递归实现其实是我们理解计算机，或者说编程语言中关于函数调用的方式最好的方式之一，它让我们知道了某种编程语言在实现函数调用的方式，也是计算机进程切换的一种思想的体现。

我们先来说说汉诺塔问题：

汉诺塔问题是一个经典的问题。

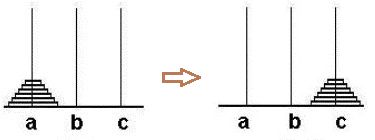
汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？

递归实现

我们先来看看汉诺塔问题的递归解决思路：

1. 将 a 上的 n-1 个盘子通过以 c 为辅助移动到 b
2. 将 a 上剩余的最大的盘子直接移动到 c
3. 将 b 上的 n-1 个盘子通过 a 为辅助移动到 c

这其实是我们说过无数次的递归思路，代码实现很简单：

// 递归实现汉诺塔
// n 为汉诺塔圆盘编号，从小到大为 1，2，3，……
void hanoi(int n, char A, char B, char C) {
    if(n == 1) {
        printf("%c -> %c\n", A, C);  // 如果只有一个盘子，从 A 直接移动到 C
    }else {
        hanoi(n-1, A, C, B);    // A 上的盘子，以 C 为辅助，移动到 B
        hanoi(1, A, B, C);      // 移动 A 上的最大的盘子到 C 上
        hanoi(n-1, B, A, C);    // 将 B 上的盘子以 A 为辅助，移动到 C
    }
}

递归时候的思路很清晰明了，我们可以通过 debug 看到函数栈的调用，每个函数帧保存了当前函数所需要的参数，当函数栈顶层的函数都执行完毕时，这个函数被弹出pop，然后根据所保存的信息来执行。

非递归实现

而非递归实现，其实也就是需要我们手动模拟出函数栈，需要用函数栈保存一些参数。
我们可以定一个结构体 Status 来保存当前状态的参数，随后当 pop 到这个函数时就可以直接读取使用。
不光是汉诺塔的非递归实现，包括我们的 BFS 的实现，其实也是使用栈来保存当前的状态信息，我们都可以使用一个 Status 来保存。

// 保存函数状态
struct Status {
    int n;
    char start, mid, end;   // 初始塔，辅助中间塔，最终要移动到的塔
    Status(int _n, char _A, char _B, char _C): n(_n), start(_A), mid(_B), end(_C) {}
};

而栈的使用又有一个特点，那就是 FILO，也就是先进后出，所以我们需要按照递归函数调用的反向来保存状态，也就是先调用的后 push 到栈中。
从而我们得到了非递归的实现。

// 采用非递归实现汉诺塔问题
// 由于栈的特殊性质，FILO，所以我们需要将原来函数的调用方式反过来进行
void hanoiStack(int n, char A, char B, char C) {
    stack<Status> myS;
    myS.push(Status(n, A, B, C));
    while (!myS.empty())
    {
        Status ns = myS.top();
        myS.pop();
        if(ns.n == 1) {
            printf("%c -> %c\n", ns.start, ns.end);
        }else {
            myS.push(Status(ns.n-1, ns.mid, ns.start, ns.end));    
            myS.push(Status(1, ns.start, ns.mid, ns.end));
            myS.push(Status(ns.n-1, ns.start, ns.end, ns.mid));   
        }
    }
}

思考

我们通过非递归解决方式得到了一种递归问题的另外一种解决方法，在我们手动去写递归函数的时候，其实是操作系统或者说编程语言帮助我们实现了函数栈，帮助我们保存了每次使用所需要的参数。
而且在很多时候，非递归的实现方式可以帮助我们节省系统资源，帮助我们节约宝贵的系统资源。