OO第一单元总结——惊蛰

前言

相传，战国时代，
雷神山有一对同门师兄弟——善逸 和 狯岳 。
他们正在切磋剑道，狯岳先出招：
狯岳：雷之呼吸，二之型，输入
狯岳：雷之呼吸，三之型，处理
狯岳：雷之呼吸，四之型，输出
善逸：雷之呼吸，一之型，面向对象！
狯岳（败）：苏卡布列！为啥这家伙只会这一招，速度却能比我快这么多！
善逸回答：集中一点，登峰造极

一、分析程序结构

第一次作业

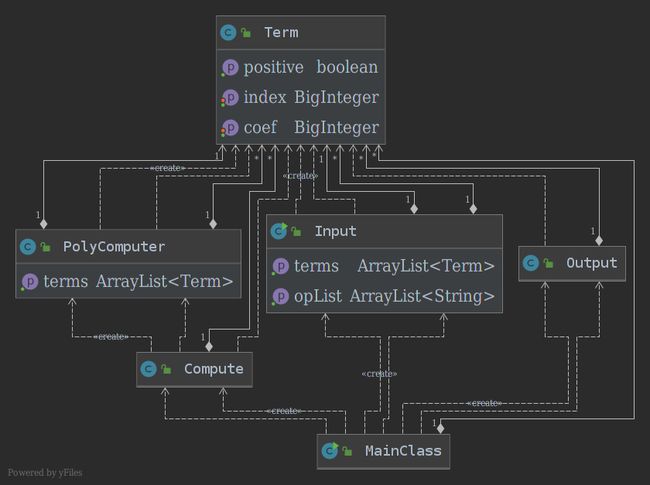
1. 度量类的属性个数、方法个数、每个方法规模、每个方法的控制分支数目、类总代码规模

类名	类的属性个数	类的方法个数	类总代码规模
Compute	0	2	14
Output	0	2	35
MainClass	0	6	30
Input	2	5	105
Term	3	8	71
PolyComputer	2	5	56

方法名	方法规模	控制分支数目	方法名	方法规模	控制分支数目
main.Compute.Compute()	4	0	poly.PolyComputer.PolyComputer()	4	3
main.Compute.run()	7	0	poly.PolyComputer.derivation()	18	0
main.Input.addTerm(Matcher)	34	5	poly.PolyComputer.getTerms()	3	3
main.Input.getOpList()	3	0	poly.PolyComputer.merge()	21	0
main.Input.getTerms()	3	0	poly.PolyComputer.run()	4	0
main.Input.main(String[])	6	0	poly.Term.Term(BigInteger,BigInteger)	4	2
main.Input.read()	31	4	poly.Term.compareTo(Term)	18	0
main.Input.store(String,String)	13	2	poly.Term.getCoef()	3	0
main.MainClass.MainClass()	2	0	poly.Term.getIndex()	3	0
main.MainClass.compute()	4	0	poly.Term.isPositive()	3	0
main.MainClass.input()	6	0	poly.Term.setCoef(BigInteger)	3	0
main.MainClass.main(String[])	4	0	poly.Term.setIndex(BigInteger)	3	0
main.MainClass.output()	4	0	poly.Term.toString()	32	7
main.MainClass.run()	5	0
main.Output.Output(ArrayList )	3	0
main.Output.run()	27	6

2. 分析类的内聚和相互间的耦合情况

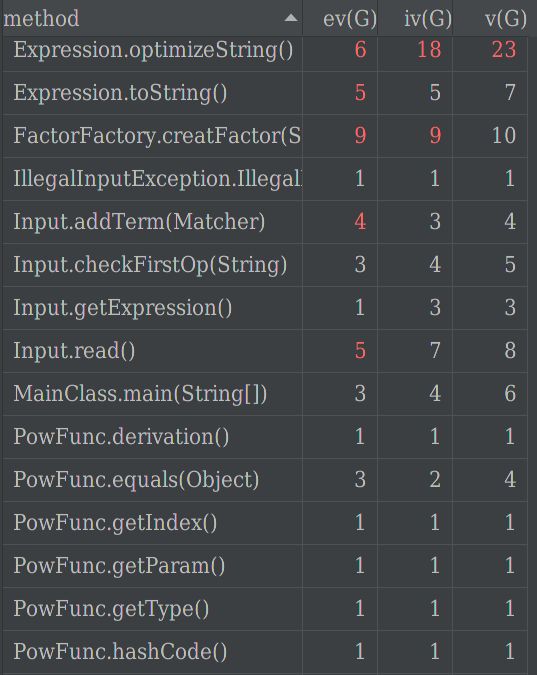
可以从下图看出，Term类的toString方法的基本复杂度、圈复杂度达到预警程度，非结构化程度过高，消除了一个错误有时会引起其他的错误。这正是导致我出bug的地方。

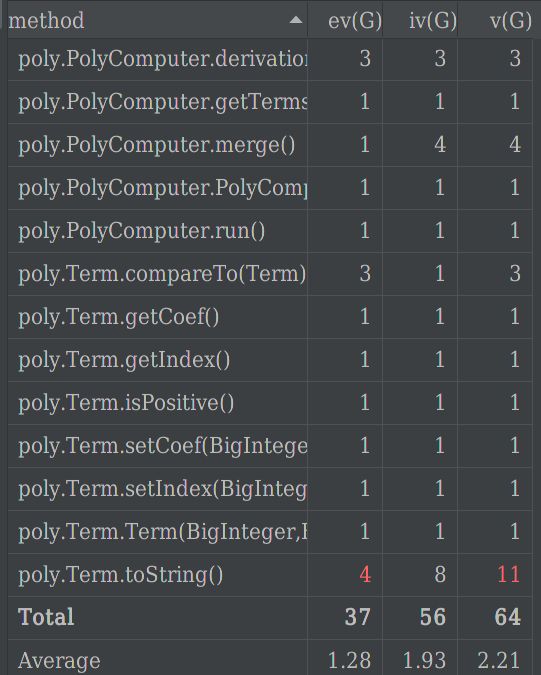
名词解释：

ev(G)基本复杂度，是用来衡量程序非结构化程度的，非结构成分降低了程序的质量，增加了代码的维护难度，使程序难于理解。因此，基本复杂度高意味着非结构化程度高，难以模块化和维护。实际上，消除了一个错误有时会引起其他的错误。

Iv(G)模块设计复杂度，是用来衡量模块判定结构，即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度，因此模块设计复杂度不能大于圈复杂度，通常是远小于圈复杂度。

v(G)圈复杂度，是用来衡量一个模块判定结构的复杂程度，数量上表现为独立路径的条数，即合理的预防错误所需测试的最少路径条数，圈复杂度大说明程序代码可能质量低且难于测试和维护，经验表明，程序的可能错误和高的圈复杂度有着很大关系。

3. DIT分析

因为本次作业的需求比较简单，只有幂函数和常数因子，就没有采用接口或者继承，抽象程度不够。

4. 类图

• 优点

  1. 把幂函数和常数因子归为一种形式，处理简单。
  2. 采用过程式思维，可以分模块测试。

• 缺点

  1. 把幂函数和常数因子归为一种形式，常数看成项的coef属性，抽象层次不够高，没有意识到常数因子是一种特殊的因子,以后的作业，项的形式变化后，就不能适用了。
  2. 采用过程式思维，竟然写了input、compute、output三个类分别处理输入、计算、输出。其实完全是冗余的代码，没有必要这么分。

第二次作业

1. 度量类的属性个数、方法个数、每个方法规模、每个方法的控制分支数目、类总代码规模

类名	类的属性个数	类的方法个数	类总代码规模
Const	5	11	52
CosFunc	4	10	63
Expression	1	12	145
Factor	3	5	7
FactorFactory	0	1	55
IllegalInputException	0	1	5
Input	1	4	96
MainClass	0	1	25
PowFunc	4	10	66
Regex	6	6	39
SinFunc	3	9	60
Term	1	22	316

方法名	方法规模	控制分支数目	方法名	方法规模	控制分支数目
Const.Const(BigInteger)	3	0	Expression.Expression()	2	0
Const.derivation()	8	0	Expression.Expression(HashSet )	3	0
Const.equals(Object)	14	2	Expression.addExp(Expression)	9	2
Const.getCoef()	3	0	Expression.addTerm(Term)	16	2
Const.getParam()	4	0	Expression.addTermWithout()	7	2
Const.getType()	4	0	Expression.allZeroTerm()	10	3
Const.hashCode()	4	0	Expression.cloneWithout(Term)	11	3
Const.isPositive()	3	0	Expression.derivation()	8	1
Const.isSpace()	4	0	Expression.getTermSet()	3	0
Const.merge(Factor)	9	1	Expression.multFactor(Factor)	7	1
Const.toString()	4	0	Expression.optimizeString()	70	17
CosFunc.CosFunc(BigInteger)	3	0	Expression.toString()	30	7
CosFunc.derivation()	13	0	FactorFactory.creatFactor(String)	45	8
CosFunc.equals(Object)	12	2	IllegalInputException.IllegalInputException()	3	0
CosFunc.getIndex()	3	0	Input.addTerm(Matcher)	24	4
CosFunc.getParam()	4	0	Input.checkFirstOp(String)	10	2
CosFunc.getType()	4	0	Input.getExpression()	13	2
CosFunc.hashCode()	4	0	Input.read()	40	7
CosFunc.isSpace()	4	0	MainClass.main(String[])	32	6
CosFunc.merge(Factor)	9	1	Term.Filt(Term)	9	2
CosFunc.toString()	12	2	Term.Term()	2	0
PowFunc.PowFunc(BigInteger)	3	0	Term.Term(HashSet )	3	0
PowFunc.derivation()	11	0	Term.addFactor(Factor)	17	3
PowFunc.equals(Object)	12	2	Term.addTerm(Term)	9	0
PowFunc.getIndex()	3	0	Term.canOptimize1(Term)	19	3
PowFunc.getParam()	4	0	Term.canOptimize2(Term)	18	2
PowFunc.getType()	4	0	Term.canOptimize3(Term)	17	2
PowFunc.hashCode()	4	0	Term.cloneWithout(Factor)	11	3
PowFunc.isSpace()	4	0	Term.contains(Factor)	4	0
PowFunc.merge(Factor)	9	1	Term.derivation()	29	2
PowFunc.toString()	16	3	Term.equals(Object)	11	2
Regex.getConstPolyTag()	3	0	Term.getConst()	8	2
Regex.getCosFuncTag()	3	0	Term.getState()	45	18
Regex.getFactorTag()	3	0	Term.hashCode()	4	0
Regex.getPowFuncTag()	3	0	Term.multTerm(Term)	6	1
Regex.getSinFuncTag()	3	0	Term.optimize1(Term)	15	0
Regex.getTerm()	3	0	Term.optimize2(Term)	16	0
SinFunc.SinFunc(BigInteger)	3	0	Term.optimize3(Term)	16	0
SinFunc.derivation()	13	0	Term.partEquals(Term)	20	6
SinFunc.equals(Object)	12	2	Term.setState()	8	0
SinFunc.getParam()	4	0	Term.toString()	72	15
SinFunc.getType()	4	0
SinFunc.hashCode()	4	0
SinFunc.isSpace()	4	0
SinFunc.merge(Factor)	9	1
SinFunc.toString()	12	2

2. 分析类的内聚和相互间的耦合情况

可以从下图看出，Term类的toString方法、getState方法和Expression类的optimizeString方法的基本复杂度、模块设计复杂度、圈复杂度达到预警程度。

• Term类的toString方法会遍历因子集合，并且根据不同的情况，需要通过Factor接口调用不同类型的因子类的转换为字符串的方法，故耦合度很高。
• 另一块耦合度过高的地方是优化最后输出的表达式。由于我的项类采用的是hashset来存储因子，表达式类采用hashset来存储项，导致最后要进行sin**2+cos**2优化的时候，必须先用getState方法遍历项的因子集合，找出常数因子以及三角函数因子，这个过程会调用大量的非Term类的方法，导致耦合度过高。此外，最后去除、合并二次三角函数的过程在Expression类的optimizeString方法中完成，这又需要调用很多Term类的方法，耦合度很高。（数据结构设计的不好是根本原因）

3. DIT分析

因为本次作业加入了三角函数求导的需求，因子种类增加了。于是就设计了Factor接口，统一因子层次的求导、合并等方法，便于项类调用。

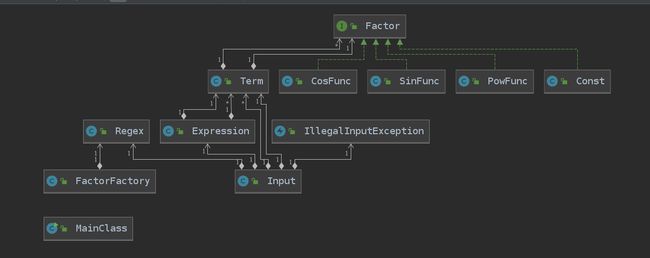
4. 类图

• 优点

  1. 把所有因子都实现一个接口，在项类的处理变得简单。
  2. 表达式树设计成了三层 Expression（表达式）--> Term （项）--> Factor（因子），层次清晰，符合常人的逻辑。
  3. 采用try -catch捕捉非法输入异常，减少冗余代码。
  4. 主类写的很简单，删掉了不必要的过程式compute类，output类。

• 缺点

  1. 优化三角函数的过程的getState方法其实就是把最后的表达式树结构转化成了4维向量结构，还不如一开始就把数据结构设计成四维向量。
  2. 采用的是hashset作为容器，其实完全是没有必要的，可以用泛型实现更优雅的数据结构。

第三次作业

1. 度量类的属性个数、方法个数、每个方法规模、每个方法的控制分支数目、类总代码规模

类名	类的属性个数	类的方法个数	类总代码规模
Regex	0	0	36
CosFunc	4	11	95
Term	2	24	317
Expression	1	18	157
Const	5	12	55
FactorFactory	0	2	109
PowFunc	4	11	59
ExpParser	1	6	126
SinFunc	4	10	92
ExpFunc	5	13	84
Factor	3	6	8
MainClass	0	2	40
IllegalInputException	0	1	5
Input	1	1	11

方法名	方法规模	控制分支数目	方法名	方法规模	控制分支数目
Const.Const(BigInteger)	3	0	Expression.hashCode()	4	0
Const.canMerge(Factor)	4	0	Expression.multExp(Expression)	12	2
Const.derivation()	8	0	Expression.multFactor(Factor)	7	1
Const.equals(Object)	14	2	Expression.multFactorRow(Factor)	6	1
Const.getCoef()	3	0	Expression.multTerm(Term)	8	1
Const.getParam()	4	0	Expression.toString()	9	1
Const.getType()	4	0	FactorFactory.check(String)	37	10
Const.hashCode()	4	0	FactorFactory.creatFactor(String)	58	14
Const.isPositive()	3	0	IllegalInputException()	3	0
Const.isSpace()	4	0	Input.getExpression()	10	1
Const.merge(Factor)	9	1	MainClass.better(String)	25	5
Const.toString()	4	0	MainClass.main(String[])	16	1
CosFunc.CosFunc(BigInteger,Factor)	4	0	PowFunc.PowFunc(BigInteger)	3	0
CosFunc.canMerge(Factor)	9	2	PowFunc.canMerge(Factor)	4	0
CosFunc.derivation()	15	0	PowFunc.derivation()	11	0
CosFunc.equals(Object)	13	2	PowFunc.equals(Object)	12	2
CosFunc.getIndex()	3	0	PowFunc.getIndex()	3	0
CosFunc.getParam()	4	0	PowFunc.getParam()	4	0
CosFunc.getType()	4	0	PowFunc.getType()	4	0
CosFunc.hashCode()	4	0	PowFunc.hashCode()	4	0
CosFunc.isSpace()	4	0	PowFunc.isSpace()	4	0
CosFunc.merge(Factor)	9	1	PowFunc.merge(Factor)	9	1
CosFunc.toString()	34	12	PowFunc.toString()	8	1
ExpFunc.ExpFunc(Expression)	18	6	SinFunc.SinFunc(BigInteger,Factor)	4	0
ExpFunc.canMerge(Factor)	4	0	SinFunc.canMerge(Factor)	9	2
ExpFunc.derivation()	8	0	SinFunc.derivation()	15	0
ExpFunc.equals(Object)	12	2	SinFunc.equals(Object)	13	2
ExpFunc.getBase()	3	0	SinFunc.getParam()	4	0
ExpFunc.getExpression()	3	0	SinFunc.getType()	4	0
ExpFunc.getParam()	5	0	SinFunc.hashCode()	4	0
ExpFunc.getType()	4	0	SinFunc.isSpace()	4	0
ExpFunc.hashCode()	4	0	SinFunc.merge(Factor)	9	1
ExpFunc.isSpace()	7	1	SinFunc.toString()	34	12
ExpFunc.merge(Factor)	13	1	Term.Filt(Term)	9	2
ExpFunc.setBase(Expression)	3	0	Term.Term()	2	0
ExpFunc.toString()	4	0	Term.Term(ArrayList )	3	0
ExpParser.ExpParser(String)	3	0	Term.addFactor(Factor)	58	14
ExpParser.addTerm(Matcher)	25	4	Term.addFactorRow(Factor)	3	0
ExpParser.checkFirstOp(String)	22	6	Term.addTerm(Term)	9	0
ExpParser.getExpression()	13	2	Term.addTermRow(Term)	9	0
ExpParser.parse(String)	36	7	Term.canOptimize1(Term)	12	3
ExpParser.parseOuterParentheses(String)	19	5	Term.canOptimize2(Term)	11	2
Expression.Expression()	2	0	Term.canOptimize3(Term)	10	2
Expression.Expression(ArrayList )	3	0	Term.checkConst()	26	6
Expression.addExp(Expression)	9	2	Term.cloneWithout(Factor)	11	3
Expression.addExpRow(Expression)	9	2	Term.contains(Factor)	4	0
Expression.addTerm(Term)	41	9	Term.derivation()	29	2
Expression.addTermRow(Term)	10	1	Term.equals(Object)	11	2
Expression.addTermWithout()	7	2	Term.getConst()	8	2
Expression.allZeroTerm()	10	3	Term.getFactorSet()	3	0
Expression.cloneWithout(Term)	13	4	Term.getState()	45	18
Expression.derivationWholeExp()	8	1	Term.hasExpFunc()	8	2
Expression.equals(Object)	11	2	Term.hashCode()	4	0
Expression.getTermSet()	3	0	Term.multTerm(Term)	6	1
			Term.multTermRow(Term)	5	1
			Term.partEquals(Term)	23	7
			Term.toString()	24	9

2. 分析类的内聚和相互间的耦合情况

其实第三次作业的输出相比第二次作业有所改变，把最后进行sin**2+cos**2优化部分删去了，这部分的耦合度本来是很高的，所以第三次作业少了一些耦合度高的部分。

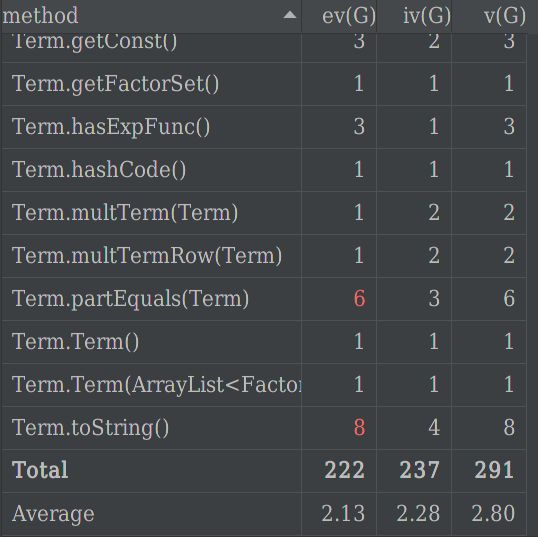
可以从下图看出，Term类的toString方法和addFactor方法,CosFunc和SinFunc类的toString方法的基本复杂度、模块设计复杂度、圈复杂度达到预警程度。

addFactor方法要完成合并同类项的过程，要调用判断、合并等属于Factor类的方法，会造成高耦合的现象。

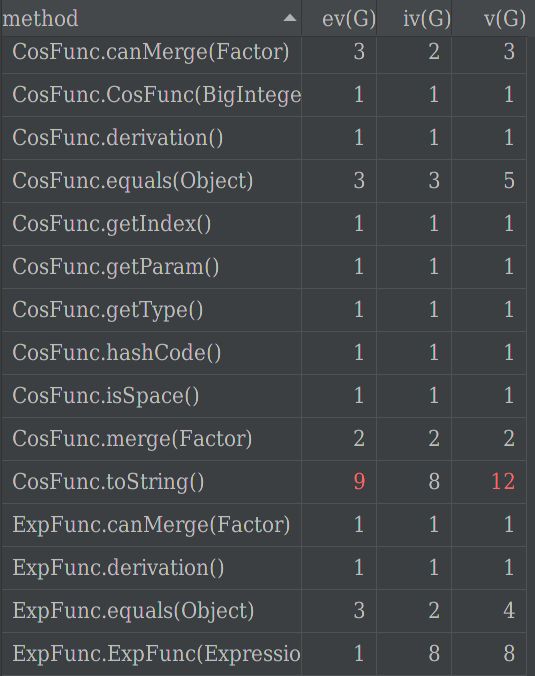
4. 类图

• 优点

  1. 使用的是ArrayList容器存储一切对象，项的成员变量是一个存储因子的ArrayList,表达式的成员变量是一个存储Term的ArrayList。表达式层次实现的是加法规则，即表达式类的ArrayList存储的对象视为相加。项层次实现的是乘法规则，项类的ArrayList存储的对象视为相乘。相比第二次作业用的HashSet,ArrayList可以存储相同的元素，可以应对多样的需求。
  2. 在因子类，实现求导的链式法则。在项类，实现求导的乘法法则。表达式类，实现求导的加法法则。求导的结果最终会由表达式树的低端依次向上传递，直至传递到最高层的表达式中。这样就可以用正常的逻辑，按部就班地挨个实现求导法则。
  3. 合并同类因子的操作：每次向项类的ArrayList中add因子时，先遍历整个ArrayList，查看是否有可以合并的因子。在Factor接口定义boolean CanMerge（Factor factor2）方法判断两个因子是否可以合并，如果是表达式因子，则返回true(因为表达式因子乘其他因子是一定可以合并的)，如果不是表达式因子，则比较是否是同类型的因子，是的话就可以根据乘法合并。在Factor接口定义Factor Merge(Factor factor2)，就是每个因子合并的时候调用的函数，返回值是合并后的Factor。最终达到在每一个表达式中只存储不能合并的项以及在每个项中存储不能合并的因子。
  4. 输入的时候就可以化简的表达式，利用加法和乘法法则，先化简好，再进入下一步的求导。这样可以减轻之后求导运算的计算负担。而且可以得到较短的结果。

• 缺点

  1. 每次向容器里添加的时候都合并同类项，这样操作的复杂度过高。所以我只在输入的时候合并同类项，求导的过程中没有合并同类项。这样可以节省很多运行时间。
  2. 表达式树是嵌套结构的，需要进行很多次递归，一旦结构设计不慎，就会出现运行时间错误或者栈溢出等错误。

二、分析自己程序的bug

第一次作业

bug位置

在输出的时候，没有考虑周全。

项的toString方法把系数为0的项都变成空字符。但是项全是0的时候，要输出“0”，我的做法会导致项全是0的时候输出空字符。本来在写output类的时候，我想到了会出现这种情况，于是就打算先把terms里面的空字符过滤掉，再判断terms是不是空，是空就输出“0",不是空，就正常输出。

结果后来忘记写过滤空字符的方法了。

自己测试的时候也忽略了系数为0的项的边界测试，仅仅是用了室友分享的一些测试用例，覆盖性不够。

最终导致互测被找出4次错误。

设计的问题

我的设计问题在于：不仅写了多项式的toString方法，还专门写了一个output类处理输出。结果本该在项类的toString方法里完成的空字符过滤被割裂在两个类里，导致自己单看一个类的时候意识不到错误。

这是面向对象思想和面向过程思想杂糅导致程序的逻辑混乱。

自己对多项式这个对象的抽象程度还不够高，应该遵循高内聚的思想，放弃以前过程式的思维。

感想

经历了第一次作业，我对自己的记性产生了严重怀疑。于是能够变颜色的注释//TODO成为了我代码里不可或缺的一部分。每次写一个情况比较多的方法，都会加一个//TODO注释，警告自己有那些遗漏的情况没有考虑。每次提交前，我都会在检查一遍那些//TODO注释的地方。

在之后的两次作业里，我开始重视自己的测试。用自动评测机进行随机测试，结合0指数、0系数、系数上下界等边界条件做手动测试。

第二次作业

bug位置

判断空白字符出现错误。会漏判WF。

由于第二次作业指导书降低了难度，不会由空白字符带来格式错误，于是我打算先把空白字符过滤掉。

对于输入的原始表达式，我会先调用一个String.replaceAll("\\s","")过滤。

然而这是不对的，正则表达式里定义的\s并不是指导书定义的空白字符。

指导书定义空白字符是 空格|\t，但是\s 其实是[ \f\n\r\t\v]，所以会把非法字符\f\r\v全都过滤掉，导致发现不了非法字符导致的WF。

设计的问题

我的设计问题在于：在过滤的时候没有考虑后果。

其实对于输入格式的判断有更好的方法。那就是：先检查是否含有非法字符，再过滤掉非法字符。我在第三次作业里就采用了这个思路。

感想

要好好阅读指导书，对于形式定义要严谨，不能想当然。

第三次作业

bug位置

常数因子解析过程漏了空白符。会错判WF。

设计的问题

我处理输入的方法是：对于输入的String，先用ExpParser进行预处理（把最外层括号替换掉），再解析预处理好的字符串，在表达式中根据+-截断，在项中根据*截断，并最终给因子进行因子匹配，如果任何一个过程匹配失败，就抛出异常，由主类捕捉，报WF。

匹配到了括号就利用String.substring(1，str.length()-1)将外层的两个括号去掉，创立一个新的表达式因子，再次利用ExpParser解析括号里的内容，相当于表达式树深度增加一层，最终递归到最底层（即没有括号，就真的是作业二类型的表达式了）。

这样的方式要求每个因子的匹配都是完全匹配，所以我对着指导书，把每个因子的形式表示都写成正则表达式。空白字符也是在能加上的地方就加上。虽然和指导书定义不同，我在因子末尾我都加了空白字符。当时认为常数因子比较特殊，按照指导书来才好，所以唯独常数因子末尾没有加空白符。

最后问题出在：匹配与捕获的内容不同，我在项的Pattern里面会把因子末尾的空格匹配到。但是捕捉的时候，是按因子的Pattern捕捉的，由于常数因子末尾没有加空白符，所以捕捉不到完整的常数因子，会在末尾留下空格。再次匹配的时候，空格是无法匹配的，就会报WF。

感想

要注意统一正则表达式匹配和捕获的内容。

三、发现别人程序bug所采用的策略

自动评测机

借鉴了讨论区任杰瑞同学的脚本写作思路，以及陈天异同学的判断正误的方法，感谢你们的分享！

用python的xeger包自动生成表达式，并且用sympy.diff对生成的表达式求导，再把同学的java程序的求导结果输入judge.py程序进行一定范围内逐个数据点的比较，错误的时候就把原表达式写入一个WA.txt文件。

我写了一个linux shell脚本，python3 generate.py生成一个表达式作为测试数据写入input.txt，并且把8个人的代码都用IDEA打包为jar包，利用for循环遍历，python3 judge.py判断表达式正误。所以一次性会测所有人代码，只需要等这WA.txt出现内容就好。

#directory list
p[0]=./Saber
p[1]=./Lancer
p[2]=./Archer
p[3]=./Rider
p[4]=./Caster
p[5]=./Assassin
p[6]=./Berserker
p[7]=./Alterego

for ((j=0; j<5000; ++j))
do
echo -e "test case${j}:"
python3 generate.py

    for ((i=0; i<8; ++i))
    do
        cd ${p[i]}
        echo -e "\n" ${p[i]} "'s result is:"
        cat  ../input.txt | java -jar Test.jar >../output.txt
        cd ..
        out=$(cat output.txt)
        echo $out
        if [ "$out" == "WRONG FORMAT!" ];then
        	continue
        else
            python3 judge.py
        fi
        
    done
done

一般我就是把程序挂在后台，每隔2-3个小时去看一眼。

这个过程就像一个猎人把捕兽夹放在森林里，每隔一两天去看一下有无猎物被夹住。

手动评测机

自动生成的测试数据没有针对性，有时还是需要对症下药的。shell脚本还是与自动评测机差不多的思路，只是把自动生成测试数据，改为手动输入罢了。只需要把python3 generate.py改成read case，echo $case > input.txt 就可以手动测试了，一次性由终端输入一个表达式，测试8个同学是否正确。

四、应用对象创建模式

本单元的作业主要运用的是工厂模式。

由于第一次作业我把对象只分成了一类，没有使用工厂模式，导致第二次作业进行了大量重构。

第二次作业就开始有三角函数加入，对象的类型变得多起来，运用工厂模式可以很好地解决创建对象的困难。

第三次作业沿用第二次的工厂模式，并改进了工厂的流程。

五、对比和心得体会

对比优秀代码

在周三的研讨课听了各位同学的分享，收获很多。

• 第二次作业其实本来term可以不用hashset,简单的数组就可以了

• 本来可以用泛型，不用把put的逻辑再写一遍

• junit test 文件夹，可以测试单个public方法

心得体会

如果把OO四次作业比作一年四季，那么第一次作业就是惊蛰啦。

♪♫♬新的希望已经出现，怎么能够停止不前♪♫♬

咳咳，心得体会：

经历了三周oo作业的洗礼，在讨论区看帖子、和同学讨论、听研讨课的过程中，收获了很多新知识，接受了面向对象的设计理念。

• 我意识到了设计的重要性，磨刀不误砍柴工，写代码之前先自己在纸上画一画流程图、进行数学推演之类的。

• 我意识到了测试的重要性，不仅要黑盒测试，还要白盒测试，尽量覆盖代码的每个分支。

• 逐渐从过程式程序的思维向转变面向对象思维。