数据结构内排序之惨死攻略（二）

接上回合《数据结构内排序之惨死攻略（一）》

听闻今天还要学数据结构，心中堵着一片乌云。

就算受低潮情绪影响也要坚持学下去啊。

目录

5 归并排序

5.1 栗子

5.2 代码实现

5.3 归并算法优化

5.3.1 R.Sedgewick优化

5.3.2 R.Sedgewick代码实现

5.4 算法分析

​

6 分配排序和索引排序

6.1 桶式排序

6.1.1 栗子

6.1.2 代码实现

6.1.3 算法分析

6.2 基数排序

6.2.1 栗子1

​

6.2.2 栗子2

​

6.2.3 LSD(低位优先)-基于顺序存储

6.2.4 LSD(低位优先)-基于链式存储

​

7 总结

---

5 归并排序

简化下高考一本，二本，专科分数线的划分方式

5.1 栗子

• 划分为两个子序列
• 分别对每个子序列归并排序
• 有序子序列合并

5.2 代码实现

template

void MergeSort(Record Array[],Record TempArray[],int left,int right){
    //Array为待排序数组，left,right两端
    int middle;
    if(left < right){//序列中只有0或1个记录，不用排序
        middle = (left + right)/2;   //平分为两个子序列
        //对左边一半进行递归
        MergeSort(Array,TempArray,left,middle);
        //对右边一半进行递归
        MergeSort(Array,TempArray,middle+1,right);
        Merge(Array,TempArray,left,right,middle);//归并
    }

}

归并函数

//两个有序子序列都从左向右扫描，归并到新数组
template

void Merge(Record Array[],Record TempArray[],int left,int right,int middle){
    int i,j,index1,index2;
    //将数组暂存入临时数组
    for(j=left;j<=right;j++)
        TempArray[j] = Array[j];
    index1 = left;        //左边子序列的起始位置
    index2 = middle + 1;  //右边子序列的起始位置
    i = left;             //从左开始归并
    
    while(index1 <= middle && index2 <= right){
        //取较小者插入合并数组中
        if(TempArray[index1] <= TempArray[index2])
            Array[i++] = TempArray[index1++];
        else
            Array[i++] = TempArray[index2++];
 
    }
    while(index1 <= middle)  //只剩左序列，可直接复制
        Array[i++] = TempArray[index1++];
    while(index2 <= right)   //与上个循环互斥，复制右序列
        Array[i++] = TempArray[index2++];

}

5.3 归并算法优化

1. 对基本已排序的序列进行直接插入排序，小序列不递归
2. R.Sedgewick优化：拆分方式不变，归并时从两端开始处理，向中间推进，简化边界判断

5.3.1 R.Sedgewick优化

优化前

优化后

还是看不懂？没事，接着解析。先对左边子序列进行归并

归并时应该为

此时对右边子序列32,45进行倒置

接着

对右边子序列进行归并

对右边的子序列34'，64进行倒置

........剩下步骤同上，最终为12   34’     64  78

继续合并

右边子序列进行倒置

.......最终

5.3.2 R.Sedgewick代码实现

template

void ModMergeSort(Record Array[],Record TempArray[],int left,int right){
    //Array为待排序数组，left，right指向两端
    int middle;
    if(right-left+1 > THRESHOLD){//长序列递归,threshold阈值，临界点
        middle = (left + right)/2;
        ModMergeSort(Array,TempArray,left,middle);//左
        ModMergeSort(Array,TempArray,middle+1,right);//右
        //对相邻的有序序列进行归并
        ModMerge(Array,TempArray,left,right,middle);//归并 
    }
    else InsertSort(&Array[left],right-left+1);//小序列插入排序
}

优化的归并函数

template void ModMerge(
Record Array[],Record TempArray[],int left,int right,int middle){
    int index1,index2//两个子序列的起始位置
    int i,j,k;
    for(i = left; i <= middle; i++)
        TempArray[i] = Array[i];  //复制左边的子序列
    for(j = 1; j <= right-middle; j++)  //颠倒复制右序列
        TempArray[right-j+1] = Array[j+middle];
    for(index=left,index2=right,k=left; k<=right; k++)
        if(TempArray[index1] <= TempArray[index2])
            Array[k] = TempArray[index1++];
        else
            Array[k] = TempArray[index2--];
}

 

5.4 算法分析

漫画乱入，自娱自乐。

6 分配排序和索引排序

• 不需要进行记录间的两两比较
• 需要事先知道记录序列的一些具体情况，关键码的分布

6.1 桶式排序

• 事先知道序列中的记录都位于某个小区间段[0,m]内
• 将具有相同值的记录都分配到同一个桶中，再依次按照编号从桶中取出记录，组成一个有序序列

6.1.1 栗子

6.1.2 代码实现

template void BucketSort(Record Array[],int n,int max){
    Record *TempArray = new Record[n]; //临时数组
    int *count = new int[max]; //桶容量计数器
    int i;
    for(i=0; i=0; i--)       //局部开始，保证稳定性
        Array[--count][TempArray[i]] = TempArray[i];
}

6.1.3 算法分析

6.2 基数排序

桶式排序只适合m很小的情况。

基数排序：当m很大时，可以将一个记录的值分为多个部分来比较。

还是直接看例子吧，概念神马的先再见。

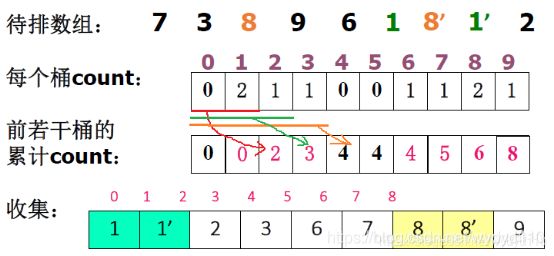
6.2.1 栗子1

---

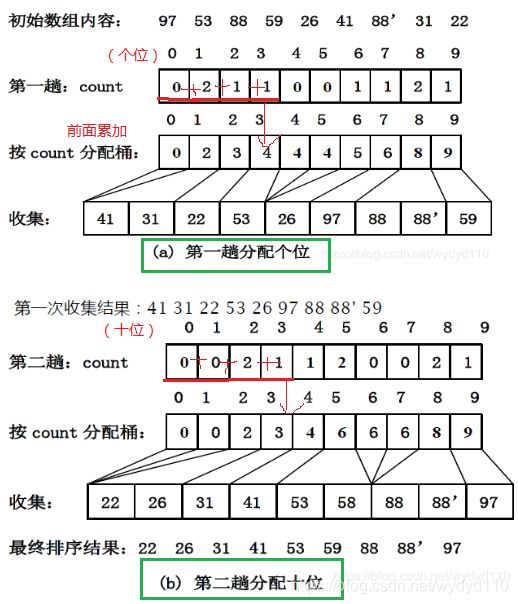
6.2.2 栗子2

---

6.2.3 LSD(低位优先)-基于顺序存储

原始输入数组 R 的长度为 n，基数为 r，排序码个数为 d

代码实现

template 

void RadixSort(Record Array[], int n, int d, int r) {
    Record *TempArray = new Record[n];
    int *count = new int[r]; 
    int i, j, k;
    int Radix = 1; // 模进位，用于取Array[j]的第i位
    for (i = 1; i <= d; i++) { 
        // 对第 i 个排序码分配 
        for (j = 0; j < r; j++) 
            count[j] = 0;   // 初始计数器均为0 
        for (j = 0; j < n; j++) { // 统计每桶记录数 
            k = (Array[j] / Radix) % r; // 取第i位 
            count[k]++; // 相应计数器加1 
         }
        for (j = 1; j < r; j++) // 给桶划分下标界 
            count[j] = count[j-1] + count[j]; 
        for (j = n-1; j >= 0; j--) { // 从数组尾部收集 
            k = (Array[j] / Radix ) % r; // 取第 i 位 
            count[k]--; // 桶剩余量计数器减1 
            TempArray[count[k]] = Array[j]; // 入桶 
        } 
        for (j = 0; j < n; j++) // 内容复制回 
            Array 中 Array[j] = TempArray[j]; 
        Radix *= r; // 修改模Radix 
     } 
}

算法分析

6.2.4 LSD(低位优先)-基于链式存储

原始输入数组 R 的长度为 n，基数为 r，排序码个数为 d

链式存储避免了空间浪费情况

代码实现（后续补）

算法分析

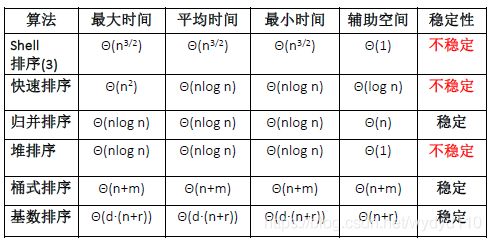
7 总结

 

4) 元素的移动次数与关键字的初始排列次序无关：基数排序

    元素的移动次数与关键字的初始排列次序有关：直接插入排序，冒泡排序，快速排序

5) 快速排序每一躺结束后都将至少一个元素放在最终位置。

 

内排序暂时告一段落了，然而仙气已经耗竭。

---

学习自：

张铭《数据结构》

程杰《大话数据结构》

陈越，何钦铭《数据结构》

 

附加：排序算法的舞蹈

冒泡排序：http://t.cn/hrf58M

希尔排序：http://t.cn/hrosvb，

选择排序：http://t.cn/hros6e

插入排序：http://t.cn/hros0W

快速排序：http://t.cn/ScTA1d

归并排序：http://t.cn/Sc1cGZ