第一单元博客作业

基于度量的程序结构

指标解析

由于第一次使用MetricsReloaded等分析工具，故首先列举一些评价指标

project层次

• v(G)avg平均圈复杂度

• v(G)tot总圈复杂度

• CF整个project的耦合程度

class层次

• OCavg代表类的方法的平均循环复杂度

• WMC代表类的方法的总循环复杂度。

• LOC类的总行数

• CBO类的耦合程度

• LCOM类的内聚程度

method层次

• ev(G)基本复杂度，是用来衡量程序非结构化程度的，非结构成分降低了程序的质量，增加了代码的维护难度，使程序难于理解。因此，基本复杂度高意味着非结构化程度高，难以模块化和维护。实际上，消除了一个错误有时会引起其他的错误。

• Iv(G)模块设计复杂度，是用来衡量模块判定结构，即模块和其他模块的调用关系。软件模块设计复杂度高意味模块耦合度高，这将导致模块难于隔离、维护和复用。模块设计复杂度是从模块流程图中移去那些不包含调用子模块的判定和循环结构后得出的圈复杂度，因此模块设计复杂度不能大于圈复杂度，通常是远小于圈复杂度。

• v(G)圈复杂度，是用来衡量一个模块判定结构的复杂程度，数量上表现为独立路径的条数，即合理的预防错误所需测试的最少路径条数，圈复杂度大说明程序代码可能质量低且难于测试和维护，经验表明，程序的可能错误和高的圈复杂度有着很大关系。

第一次作业

project层次

project	v(G)avg	v(G)tot	CF
project	2.21	42.0	0.5

class层次

class	OCavg	WMC	LOC	CBO	LCOM
Test	1.0	1.0	7.0	0.0	1.0
Term	2.1	21.0	98.0	2.0	1.0
MainClass	1.0	1.0	8.0	2.0	1.0
Polynomial	2.5	10.0	49.0	3.0	1.0
Read	3.0	9.0	45.0	3.0	1.0
Total		42.0	207.0
Average	2.21	8.4	41.4	2.0	1.0

method层次

method	ev(G)	iv(G)	v(G)
MainClass.main(String[])	1.0	1.0	1.0
Polynomial.addTerm(Term)	1.0	2.0	2.0
Polynomial.Derivative()	3.0	2.0	3.0
Polynomial.Polynomial()	1.0	1.0	1.0
Polynomial.print()	1.0	3.0	4.0
Read.getPolynomial(String)	3.0	3.0	4.0
Read.isNeg(String)	3.0	1.0	4.0
Read.main(String[])	1.0	1.0	1.0
Term.addCo(BigInteger)	1.0	1.0	1.0
Term.compareTo(Term)	2.0	2.0	2.0
Term.getCo()	1.0	1.0	1.0
Term.getDeg()	1.0	1.0	1.0
Term.getString()	5.0	6.0	8.0
Term.isNeg()	1.0	1.0	1.0
Term.setCo(BigInteger)	1.0	1.0	1.0
Term.setDeg(BigInteger)	1.0	1.0	1.0
Term.Term(BigInteger,BigInteger)	1.0	1.0	1.0
Term.Term(String,String,boolean)	1.0	2.0	4.0
Test.main(String[])	1.0	1.0	1.0
Total	30.0	32.0	42.0
Average	1.58	1.68	2.21

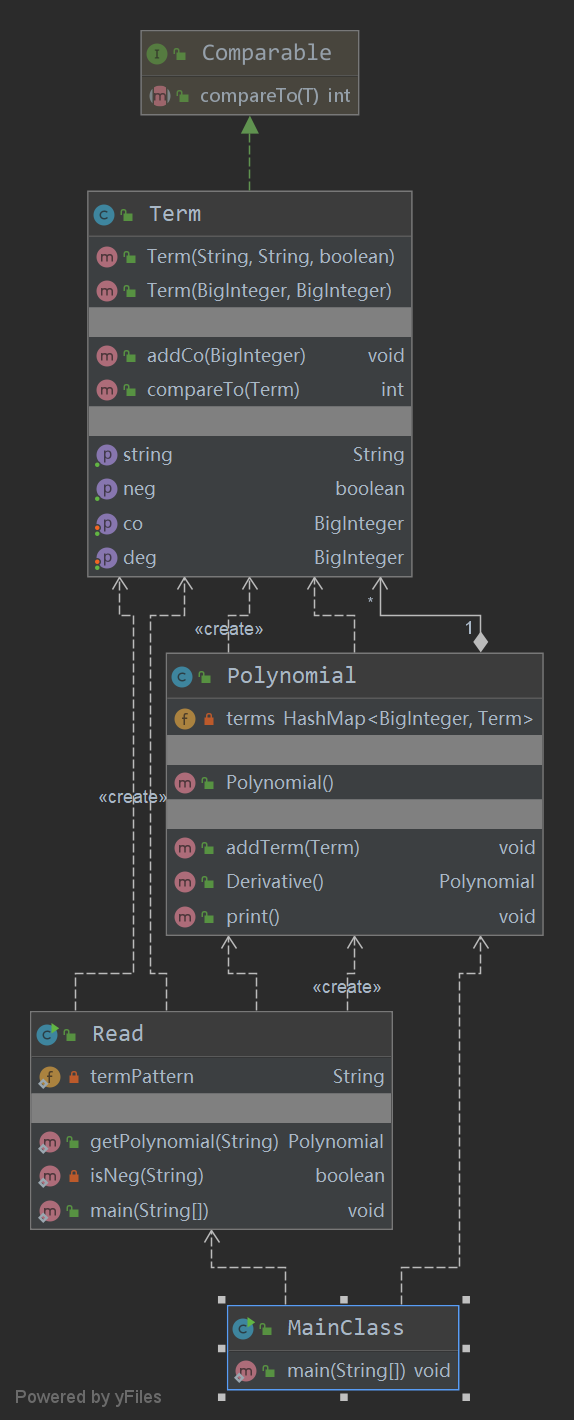
类图

 

 

• 其中Term.getString()的ev(G)基本复杂度指标偏大被标红，主要是由于我将输出的化简逻辑放在其中，直接输出化简后的字符串。这种不改变结构直接改变输出的化简方式在第一次作业中其实是可取的，但确实逻辑较复杂，模块化和维护效果不好，可以对这一块的逻辑进行拆解，分成几个方法。更好的方法是加一个化简类进行化简和输出，这样可以让输出的逻辑聚合度更高。

• 从类图可以看出整个结构还是比较清晰。

第二次作业

project层次

project	v(G)avg	v(G)tot	CF
project	3.19	99.0	0.67

class层次

class	OCavg	WMC	LOC	CBO	LCOM
Tuple	1.0	3.0	14.0	1.0	2.0
MainClass	2.0	2.0	21.0	3.0	1.0
Polynomial	2.3	23.0	95.0	4.0	2.0
Term	2.6	26.0	133.0	3.0	1.0
Simplify	3.75	15.0	103.0	4.0	1.0
Read	7.33	22.0	136.0	3.0	1.0
Total		91.0	502.0
Average	2.94	15.17	83.67	3.0	1.33

method层次

method	ev(G)	iv(G)	v(G)
MainClass.main(String[])	2.0	2.0	2.0
Polynomial.addPolynomial(Polynomial)	1.0	2.0	2.0
Polynomial.addTerm(Term)	3.0	4.0	4.0
Polynomial.clone()	1.0	2.0	2.0
Polynomial.Derivative()	1.0	2.0	2.0
Polynomial.getLength()	1.0	1.0	1.0
Polynomial.getSize()	1.0	1.0	1.0
Polynomial.getTerms()	1.0	1.0	1.0
Polynomial.Polynomial()	1.0	1.0	1.0
Polynomial.removeTerm(Term)	1.0	1.0	1.0
Polynomial.toString()	7.0	5.0	8.0
Read.getFactor(String,String,String,String)	9.0	5.0	10.0
Read.getPolynomial(String)	7.0	8.0	11.0
Read.isNeg(String)	2.0	1.0	3.0
Simplify.findRelation(Polynomial)	5.0	7.0	8.0
Simplify.Merge(Polynomial)	1.0	4.0	4.0
Simplify.onePass(Polynomial)	2.0	4.0	4.0
Simplify.work(Polynomial,Tuple)	1.0	1.0	1.0
Term.clone()	1.0	1.0	1.0
Term.Derivative()	1.0	4.0	4.0
Term.getCoefficient()	1.0	1.0	1.0
Term.getIndexCos()	1.0	1.0	1.0
Term.getIndexSin()	1.0	1.0	1.0
Term.getIndexX()	1.0	1.0	1.0
Term.isSimilarItem(Term)	1.0	3.0	3.0
Term.Multiply(Term)	1.0	1.0	1.0
Term.Term(BigInteger,BigInteger,BigInteger,BigInteger)	1.0	1.0	1.0
Term.toString()	4.0	15.0	16.0
Tuple.getLeft()	1.0	1.0	1.0
Tuple.getRight()	1.0	1.0	1.0
Tuple.Tuple(int,int)	1.0	1.0	1.0
Total	63.0	84.0	99.0
Average	2.03	2.71	3.20

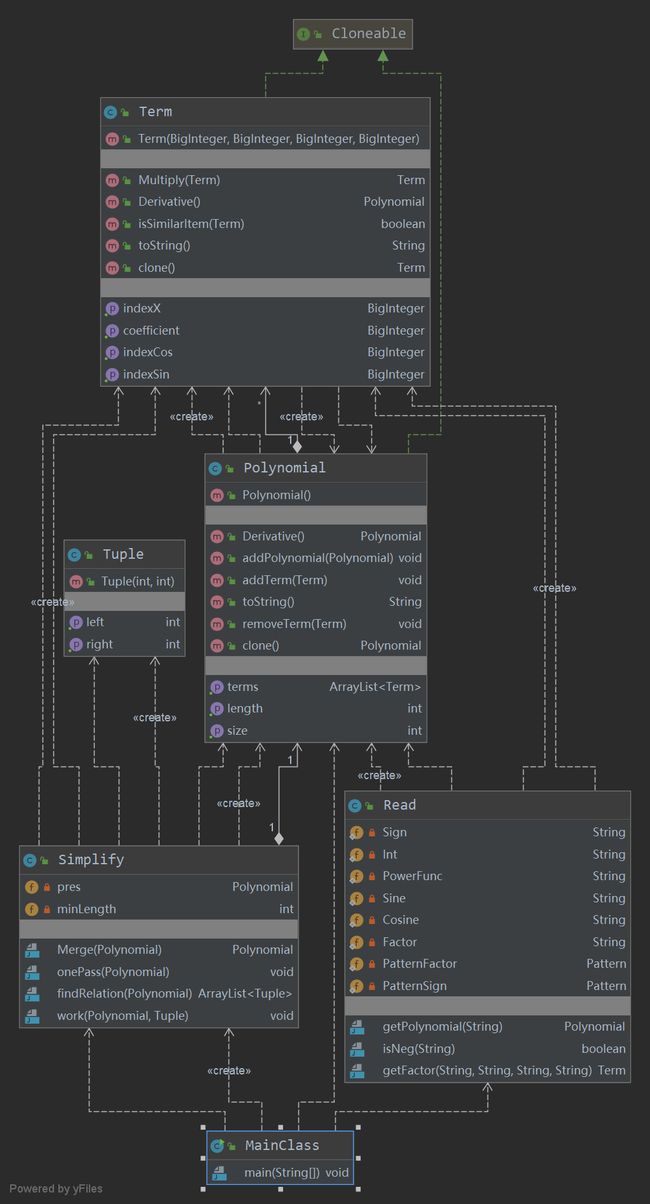
类图

 

 

• 本次作业中Polynomial.toString()和Term.toString()方法的复杂度明显较高，其目的都是化简并输出结果，延续了第一次作业的思路。修改思路同上。

• 另外Read.getPolynomial(String)和Read.getFactor(String,String,String,String)方法的复杂度也很高。原因在于解析字符串自身的复杂性，以及在分配每个方法时没有很好的遵循高内聚低耦合的原则。getFactor事实上包含了得到幂函数因子，常数因子，三角函数因子的所有可能情况，可以考虑将其分开来进行重构。

• Simplify.findRelation(Polynomial)复杂度较高，这个方法用于在化简时寻找可以化简的两项，如10*x*sin(x)**2和9*x*cos(x)**2两项存在化简可能，于是存在Relation，被这个方法找出。其设计满足高内聚低耦合的理念，结构化程度较低是由于化简本身的逻辑繁琐决定。

• 与第一次作业相比，平均圈复杂度提升，project耦合程度提高，结合类图分析，主要是由于化简模块较复杂，需要不停地创建其他类的对象，故虽然复杂度提高，结构上仍然可以接受。

第三次作业

project层次

project	v(G)avg	v(G)tot	CF
project	3.06	159.0	0.54

class层次

class	OCavg	WMC	LOC
Tuple	1.0	3.0	14.0	2.0	2.0
MainClass	2.5	5.0	39.0	3.0	1.0
Sum	2.0	8.0	34.0	4.0	1.0
Factor	1.0	2.0	10.0	4.0	1.0
Power	1.25	5.0	25.0	6.0	1.0
Constant	1.0	4.0	18.0	7.0	2.0
Sine	1.6	8.0	39.0	7.0	1.0
Cosine	1.6	8.0	39.0	7.0	1.0
Product	2.25	9.0	39.0	8.0	1.0
Simplifier	5.86	41.0	173.0	9.0	2.0
Read	4.58	55.0	280.0	10.0	1.0
Polynomial		0.0	4.0	12.0	1.0
Total		148.0	714.0
Average	2.85	12.33	59.5	6.58	1.25

method层次

method	ev(G)	iv(G)	v(G)
Simplifier.mergeProduct(ArrayList)	1.0	3.0	3.0
Read.isValidIndex(BigInteger)	1.0	2.0	2.0
Constant.Constant(BigInteger)	1.0	1.0	1.0
Sine.getGx()	1.0	1.0	1.0
Power.getIndex()	1.0	1.0	1.0
Product.getPolynomials()	1.0	1.0	1.0
Tuple.Tuple(String,Polynomial)	1.0	1.0	1.0
Simplifier.Recursive(ArrayList)	1.0	2.0	2.0
Sum.getPolynomials()	1.0	1.0	1.0
Cosine.Cosine(BigInteger,Polynomial)	1.0	1.0	1.0
Cosine.getGx()	1.0	1.0	1.0
Read.ParseConstant(String)	1.0	1.0	1.0
Read.getGx(String)	1.0	7.0	7.0
Factor.toString()	1.0	1.0	1.0
Read.ParseSinCos(String,String,Polynomial,String)	1.0	4.0	6.0
Tuple.getPolynomial()	1.0	1.0	1.0
Sine.toString()	1.0	4.0	4.0
Read.isNeg(String)	1.0	1.0	2.0
Constant.getValue()	1.0	1.0	1.0
Sum.Sum(ArrayList)	1.0	1.0	1.0
Read.ParsePower(String)	1.0	2.0	3.0
Sine.Sine(BigInteger,Polynomial)	1.0	1.0	1.0
Power.Derivative()	1.0	1.0	1.0
Factor.Derivative()	1.0	1.0	1.0
Sine.getIndex()	1.0	1.0	1.0
Cosine.getIndex()	1.0	1.0	1.0
MainClass.printPolynomial(Polynomial)	1.0	2.0	2.0
Constant.toString()	1.0	1.0	1.0
Cosine.toString()	1.0	4.0	4.0
Product.Derivative()	1.0	2.0	2.0
Read.leadingSign(String)	1.0	4.0	5.0
Tuple.getString()	1.0	1.0	1.0
Cosine.Derivative()	1.0	1.0	1.0
Sine.Derivative()	1.0	1.0	1.0
Product.Product(ArrayList)	1.0	1.0	1.0
Power.Power(BigInteger)	1.0	1.0	1.0
Constant.Derivative()	1.0	1.0	1.0
Simplifier.mergeSum(ArrayList)	1.0	3.0	3.0
Sum.Derivative()	1.0	2.0	2.0
Read.hasIllegalChar(String)	1.0	1.0	1.0
Power.toString()	2.0	1.0	2.0
Sum.toString()	2.0	5.0	5.0
Simplifier.Sum(Polynomial)	3.0	5.0	6.0
MainClass.main(String[])	3.0	4.0	4.0
Simplifier.Product(Polynomial)	4.0	8.0	9.0
Product.toString()	4.0	6.0	6.0
Read.findEnd(String,int)	5.0	2.0	6.0
Simplifier.degrade(Polynomial)	6.0	6.0	6.0
Read.getFactorSinCos(String,int,String,String)	7.0	3.0	7.0
Read.getFactor(String)	8.0	7.0	9.0
Read.getPolynomial(String,boolean)	10.0	11.0	14.0
Simplifier.modify(Polynomial)	12.0	7.0	12.0
Total	106.0	133.0	159.0
Average	2.04	2.56	3.06

类图

 

 

• 复杂度较大的方法依然在解析字符串的Read类和化简的Symplify类中，由于化简和解析逻辑进一步复杂，复杂度上升难以避免。

• 由于对于表达式因子的理解不够深刻，并没有将表达式因子作为因子中的一类，而是将其与运算类并列，造成某些类中的toString方法复杂度变高，出现了一系列特判，这是在设计时思考不周导致的。

• 平均复杂度和project的耦合程度对比与第二次作业有所降低。一方面是由于第三次作业进行了重构，舍弃了第二次作业中一些投机取巧的做法，对类的布局更加合适。

 

分析自己程序的bug

1. 对于合法字符集的处理bug

   出现在第二次作业中，bug表现为当输入出现非法的空白字符时，没有输出WF，而是当做合法空白字符来处理。问题所在的类是Read类的Read.getPolynomial(String)方法，在此方法中直接将空白字符删去，造成错误。此方法是复杂度第二高的方法，位于复杂度第一的类。问题主要源于：对于指导书的阅读不够仔细，忽略了可能有空白非法字符出现的情况；由于第一次作业也是这么做的，思维惯性导致。由于理解错误也直接导致测试时忽略了这个问题。

2. 对于三角函数嵌套表达式因子化简产生的bug

   出现在第三次作业中，表现为当输出包含sin(x**2)形式的因子时化简为sin(x*x)产生错误。问题所在类为Sine类和Cosine类，出错方法为toString方法，其复杂度不高。这次错误并没有出现在逻辑密集区，我认为主要是因为设计不足造成的实现困难造成的。如前面的分析，设计上有如下漏洞：没有将表达式因子作为因子中的一类，而是将其与运算类并列；在化简时只化简输出，不改变结构。尤其第二点给了我很大的启发，当输出已经脱离结构时，很难发现问题。另外，由于手动编测试集，手动检验的局限性，在自行测试时没有测出这个问题。

3. 部分化简造成的TLE

   出现于第三次作业，表现为面对特定的输入会超时，如-x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x-(x))))))))))))))递归层数较多，出现问题。经过分析，问题主要在于Symplify化简类，此类复杂度较高，容易出现漏洞。分析主要原因如下：没有将表达式因子作为因子中的一类，而是将其与运算类并列，在化简时特殊处理，造成sin和cos嵌套递归没有出现问题，()递归出现问题的情况；由于在设计化简时比较宽松，考虑了一部分，没考虑一部分，当没考虑的那一部分反复运行不需要的那一部分的化简代码时可能会出现超时情况，若不化简则没有这类问题；测试时覆盖不够完全。

分析自己发现别人程序bug所采用的策略

测试策略

• 三次作业都采用了手动构造测试数据并手动验证的方法。第二第三次作业用到了python辅助，但总体来讲仍是手动。

• 对于每一次作业，结合指导书中的每一个语言细节和形式化描述，尽可能多地从以下多个维度来构造样例：

  1. 正确识别输入维度

     • 合法字符集是否定义正确

     • 空白字符位置是否考虑到位

     • 特殊形式与一般形式是否考虑完善

     • 输入的特殊限制（指数范围等）

     • WrongFormat是否能正确识别

  2. 正确求导维度

     • 每个因子求导是否正确（常数因子，幂函数因子，sin因子，cos因子）

     • 求导因子的组合求导是否正确（乘积，和，表达式因子嵌套）

  3. 正确化简维度

     • 分析化简过程，找到漏洞。

     • 测试可能TLE的数据

  4. 操作维度

     • 针对代码中出现的特殊操作设置测试点（如合并同类项操作测试）

分析

• 手动构造测试数据

  • 优势：如果题目要求清晰，逻辑顺畅，手动构造能较好地针对边界数据，特殊情况。如果被测代码出现了测试集中没有涉及的操作，可以针对。

  • 劣势：构造花费时间长。全覆盖难度高。考验对题目的理解，如果理解有误，测试自然无效。

• 手动测试

  • 优势：只需目测，适应任何情况

  • 劣势：遇到五花八门的化简难以判断正确性，需要程序辅助。速度慢。

小结

• 总体上来讲，运用手动构造测试数据+手动测试的方法可以达到还不错的找bug效果。对于中等质量的代码，这种方法似乎比一些针对性不强的自动生成测试集+自动测试的方法要好。在第三次作业中，由于遇到的代码质量不高，共互测出44个bug。

• 从另一个角度，自动生成测试数据有其优势，比如我自己的化简错误。当没有挖掘到隐藏的易错点时，自动生成测试数据+自动测试可以很好地弥补这一点

• 但自动测试往往编写有一定难度，且真实状况中很难有一个第三方来验证正确性，三角函数的计算是一个特例，有很多现成的工具。所以在未来的测试中，主要考虑加入自动生成测试集的方法，视情况自动测试。

应用对象创建模式来重构

• 在三次作业中均没有使用工厂模式，虽然学习了简单工厂，工厂方法和抽象工厂模式，但是对其具体的优势体会并不深入。

• 我认为工厂模式的优势

  1. 解耦合，将对象创建与使用分开

  2. 创建对象需要参数太多时，用于隐藏参数

  3. 创建对象的参数准备过于复杂时，可以给工厂管理

  4. 仅仅关心返回的接口方法,不必关心实现细节

  5. 修改时更加方便

• 因此，当需求不断变动时，使用工厂模式可能更有优势

应用简单工厂模式的重构说明：

• 以第三次作业为例，由于作业代码量不大，且由单人完成，故只考虑使用简单工厂模式

• public class polyFactory{
      public static Polynomial createPolynomial(String type, Object ...args){
          Polynomial mPolynomial = null;
          switch (type) {
              case "Constant":
                  mPolynomial = new Constant((BigInteger)args[0]);
                  break;
              case "Sine":
                  mPolynomial = new Constant((Polynomial)args[0], (BigInteger)args[1]);
                  break;
             ......
         }
          return mPolynomial;
     }
  }

   

   

对比和心得体会

• 可以创建更多的类和方法，减少耦合。在我的代码中仍然存在复杂逻辑难以分割的情况，一个复杂的方法可能包含100行，最后再拆分成不同的方法。对于化简，解析这种非实体的类，可以将逻辑进一步细分，甚至创建更多的类以达到逻辑上的简洁。高手的方法似乎都很短。

• 第一单元的作业看似简单，但深究其细节多而杂，在上手写代码之前需要进行周密的设计，每实现一部分测试一部分。

• 在以后的测试中可以考虑用自动生成+测试。手动测试+肉眼debug在本单元的作业中太累了。

• 可以在以后的代码中加入工厂模式，万一好用呢。

• 化简需慎重，引入bug就不好了