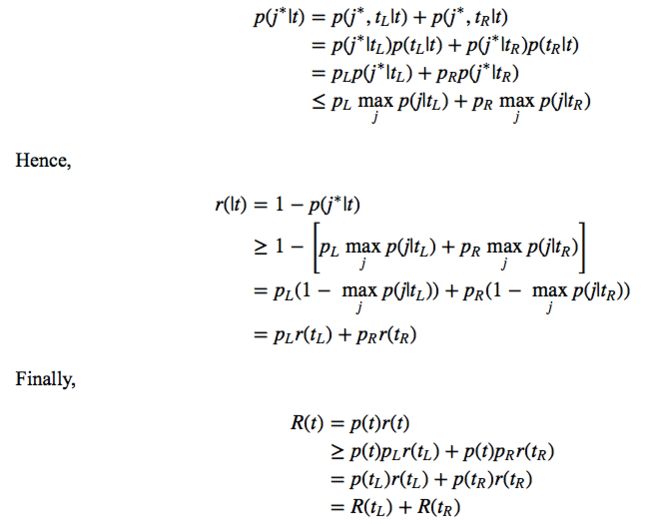第10章-基于树的方法(1)-生成树
原文参考:https://onlinecourses.science.psu.edu/stat857/node/22
一,本章简介
1,本章主要学习目标
- 理解决策树的基本概念
- 理解构成决策树的三个基本元素
- 理解’不纯度’及其他度量公式的定义
- 知道如何估计每个树节点的各个所属分类的后验概率
- 理解基于树的分类方法的优点
- 理解训练误差(或称再代入误差) 和 代价复杂度测量方法,知道它们的区别,以及为什么要介绍这种方法
- 理解 weakest-link pruning (等价代价复杂度剪枝)
- 理解剪枝后的最优子树都是互相嵌入的,可以被递归地获取
- 理解基于交叉验证来选择复杂性的参数和最终子树的方法
- 理解的model averaging目的
- 理解装袋法(bagging)的步骤
- 理解随机森林(random forest)的步骤
- 理解提升法(boosting)的步骤
决策树既可以解决回归问题也可以解决分类问题。下面我们主要关注分类问题。
分类树是与如k近邻等原型法不同的一种方法。原型法的基本思想是对空间进行划分,并找出一些具有代表性的中心。决策树也不同于线性方法,如线性的判别分析、二次判别分析和logistic回归。这些方法是用超平面作为分类边界。
分类树是对空间进行层级的划分。从整个空间开始递归地划分成小区域。最后,被划分出来的每个小区域都被赋予了一个类标签。
2,介绍(CART:Classification and Regression Trees)算法
一个医疗案例:
决策树的一个巨大的优点就是构造的分类器具有高度的可解释性。这对于医生来说是一个非常吸引人的特点。
在这个例子中,病人被分为两类:高风险vs低风险。基于最初的24小时的数据,预测为高风险的病人可能无法存活超过30天。每个病人第一个24小时内都有19个测量指标,如血压、年龄等。
下图是一个树形分类器,规则及解释如图所示:
这个分类器只关注了三个测量指标。对于一些病人,用一个指标就可以确定最终结果。所以,分类树对医生来说检验过程很简单。
10.1 构建树
我们要牢记:树代表了对空间的递归地划分。因此每一个感兴趣的节点都对应原空间的一个子区域中的节点。两个子节点占据了不同的区域,如果合并两个子节点,则合并后的区域也与父节点对应的区域相同。最后,每个叶节点都会被赋予一个分类。
树形分类器的构造就是从X空间自身开始,不断的划分出越来越小的子空间。
定义:
我们用X定义特征空间。X是多维欧式空间。然而有些时候,一些变量可能是分类变量,如性别。CART算法的优点,就是可以用统一的方法处理数值型变量和分类型变量。而对于大多数其他分类方法来说并不具备这种优势,如LDA。
- 假设输入变量表示为:X∈X,包含p个特征, X 1 , X 2 , . . . , X p X_1,X_2,...,X_p X1,X2,...,Xp
- 用 t 表示节点, t L t_L tL代表左子节点, t R t_R tR代表右子节点。
- 树种所有节点的集合用 T 表示,所有叶节点的结合用 T̃
- 一次划分用s表示,划分的集合用S表示
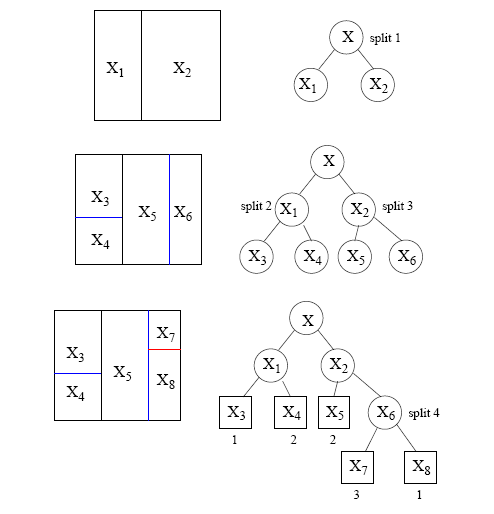
根据下图看一下,空间树如何被划分出来的:
三个基本要素
- 空间划分的选择,如在哪个节点上进行划分,以及如何划分?
- 当我们知道如何划分生成树的时候,又在何时可以确定一个终结点并停止进行划分呢?
- 我们必须对每一个终结点赋予一个类标签。那么我们又何如赋予这些标签呢?
- 标准问题集- 划分空间节点的准备
如之前所述,假定输入向量 X=(X1,X2,⋯,Xp),既包含了分类变量也包含了定序变量特征。CART算法使事情变得简单,因为每次划分仅从一个变量入手。
如果我们有定序变量,如Xj — 那么此处拆分问题可以转化为比较Xj是否小于或等于一个阈值。因此,对于任意定序变量Xj,问题集Q的统一形式如下:
{Is Xj ≤ c ?},对于任何实数 c.
当然也有其他形式的划分方法,比如,你可能想问,是否可以形如 X1+X2≤ c ? 这种情况下,划分线不是平行于坐标轴的(划分线是斜率为-1,截距为c的线)。因此,这里我们可以限制问题格式。每个问题均是取一个特征 Xj 与阈值进行比较。
因为训练集是有限的,因此只有有限多个阈值 c 对数据点进行划分。
如果 Xj 是分类变量, 取值于{1, 2, … , M}, 那么问题集Q 形如:
{Is Xj ∈ A ?},其中,A 是 {1, 2, … , M} 的子集.
所有p个特征向量的划分或问题构成了划分的候选集合。
综上,第一步就是先确定所有的候选问题。以便在下一步构建树的时候,可以挑选在哪个节点上用哪个问题来进行划分。
- 确定划分优度-‘goodness of split’
当我们选择问题进行划分的时候,我们需要测量该问题下每一个划分的’goodness of split’。这既取决于问题的选择也取决于被划分的节点。这个’goodness of split’ 是用“不纯度”公式来测量的。
直觉地,当我们划分节点时候,我们想要使得每个叶节点的区域都更“纯”。换句话说,就是使这个划分区域中的点都尽可能多的属于同一个分类,即,该类占有绝对主导地位。
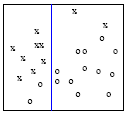
来看下面的例子。图中有两个分类,x 和 o 。划分的时候我们先检查水平变量是否高于或低于一个阈值,如下图
划分被蓝线标注。切记我们候选划分的特性,划分区总是被平行于坐标轴的线所分割的。就上面的例子说,我们会觉得是个好的划分,因为左手边比较“纯”了,基本都是 x 类,只有2列属于 o 。右手边同样比“较纯”。
直觉上选择每个划分节点的时候我们都想生成“纯”的节点。如果我们再往更深一层次探索,我们会再多两个划分,如下图
现在,如您所见,坐上区域叶节点仅包含 x 类。因此纯度是100%的,没有其他的分类出现。一旦我们达到这个水平,我们就不必再进行更近一步的划分了。因为所有的划分都是100%的纯度。在此训练集上,更多的划分不再有更好的结果,尽管可能在测试集上会有所不同。
###10.2 不纯度的测量公式
不纯度公式是用来测量包含不同分类点划分区域的“纯的程度”的。假设有K个不同的类别,那么就会有 P 1 , . . . , P k P_1,...,P_k P1,...,Pk个不纯度的测量,衡量区域中每个点归属于一个分类的概率。训练当中,我们不知道真实的概率,我们只能得到在训练集下的点属于每个分类点百分比。
不纯度的测量公式可以被定义成不同的形式,但是最基本的要要素是要满足下面的三个要素。
定义:一个不纯度的测量公式 Φ ,对于所有K 元组( P 1 , . . . , P k P_1,...,P_k P1,...,Pk),满足 ( P j > = 0 , j = 1 , . . . , K , ∑ j P j = 1 P_j>=0, j=1,...,K, \sum_j{P_j}=1 Pj>=0,j=1,...,K,∑jPj=1),且:
- Φ 值对于均匀分布将达到最大值,即当所有 P j P_j Pj 都相等时;
- Φ 值将达到最小值,当点属于某分类的概率是1,属于其他分类概率为0;
- Φ 对于( P 1 , . . . , P k P_1,...,P_k P1,...,Pk)是对称的,置换 P j P_j Pj,Φ 值不变;
定义:给定一个不纯度的测量公式 Φ ,对于 t 节点不纯度为 i(t) :
i(t)=Φ( p(1|t),p(2|t),…,p(k|t) )
式中,p(j|t) 是给定节点t中的一个点为 j 类的后验概率估计。一旦我们知道了i(t),我们就可以定义对于节点 t ,划分优度,定义为 Φ(s, t):
Φ ( s , t ) = △ i ( s , t ) = i ( t ) − P R ∗ i ( t R ) − P L ∗ i ( t L ) Φ(s, t)=△i(s,t) = i(t)-P_R *i(t_R)-P_L *i(t_L) Φ(s,t)=△i(s,t)=i(t)−PR∗i(tR)−PL∗i(tL)
式中,可以看出 Δi(s, t) 是节点 t 的不纯度,与左右子节点不纯度加权求和之间的差值。权值 P R , P L P_R ,P_L PR,PL是节点t中样本被各自划分到左右子节点的比例。
假设紫色阴影的左侧区域要被继续划分,上半部分(x)是左侧子节点,下半部分(o)是右侧子节点。那么此时左侧子节点的比例为8/10,右侧为2/10.
分类树算法会遍历所有候选划分集,找到最大△i(s,t)对应的最优划分。
接下来我们定义 I(t) = i(t) p(t), 即,节点t 的加权不纯度值。 p(t)与上述中左右子节点的权值定义一致。当然如果节点t 是总体的第一个划分得到的子节点,那么权值是总体的样本中被被划分到节点t 的样本的占比。
那么对于一个树T,不纯度的总测量定义为 , I(T):
I ( T ) = ∑ t ∈ T ′ I ( t ) = ∑ t ∈ T ′ i ( t ) ∗ p ( t ) I(T)=\sum_{t∈T'}{I(t)} = \sum_{t∈T'}{i(t)*p(t)} I(T)=∑t∈T′I(t)=∑t∈T′i(t)∗p(t)
这是所有叶节点的加权求和,注意不是所有节点,是叶节点集合T’。
且对于任何节点有:
p ( t L ) + p ( t R ) = p ( t ) p(t_L)+p(t_R)=p(t) p(tL)+p(tR)=p(t)
p L = p ( t L ) / p ( t ) ; p R = p ( t R ) / p ( t ) p_L=p(t_L)/p(t) ; p_R=p(t_R)/p(t) pL=p(tL)/p(t);pR=p(tR)/p(t)
p L + p R = 1 p_L+p_R=1 pL+pR=1
进而,我们定义一个父节点与两个子节点之间的不纯度之差:(我们得到了一个递归公式)
△ I ( s , t ) = I ( t ) − I ( t L ) − ( t R ) △I(s,t)=I(t)−I(t_L)-(t_R) △I(s,t)=I(t)−I(tL)−(tR)
= p ( t ) i ( t ) − P t L i ( t L ) − P t R i ( t R ) p(t)i(t)−P_{t_L}i(t_L)-P_{t_R}i(t_R) p(t)i(t)−PtLi(tL)−PtRi(tR)
= p ( t ) i ( t ) − p ( t ) P L i ( t L ) − p ( t ) P R i ( t R ) p(t)i(t)−p(t)P_Li(t_L)-p(t)P_Ri(t_R) p(t)i(t)−p(t)PLi(tL)−p(t)PRi(tR)
= p ( t ) △ i ( s , t ) p(t)△i(s,t) p(t)△i(s,t)
最后,我们揭开了不纯度度量的神秘面纱…
要知道,不论我们如何定义不纯度公式,我们在分类树种使用它的过程是保持一致的。所以,唯一不同的就是具体的不纯度度量公式。
不纯度的公式也分别对应不同的决策树算法
| 不纯度公式 | 对应的决策树算法 | 说明 |
|---|---|---|
| 熵: ∑ j = 1 k − p j ∗ l o g ( p j ) \sum_{j=1}^k{-p_j*log(p_j)} ∑j=1k−pj∗log(pj) 条件熵: H ( Y H(Y H(Y| X ) = ∑ i = 1 n − P ( x = x i ) ∗ H ( Y X)= \sum_{i=1}^n{-P(x=x_i)*}H(Y X)=∑i=1n−P(x=xi)∗H(Y| X = x i ) X=x_i) X=xi) 信息增益: g ( D , A ) = H ( D ) − H ( D g(D,A)=H(D)-H(D g(D,A)=H(D)−H(D| A ) A) A) |
ID3 | 用信息增益选择属性时偏向于选择分枝比较多的属性值,即取值多的属性 |
| 信息增益率: g r ( D , A ) = g ( D , A ) / I V ( A ) gr(D,A)=g(D,A)/IV(A) gr(D,A)=g(D,A)/IV(A) I V ( A ) = IV(A)= IV(A)= |
C4.5 | 对ID3算法的改进 (1)用信息增益比来选择属性 (2)在决策树的构造过程中对树进行剪枝 (3)对非离散数据也能处理 (4)能够对不完整数据进行处理 |
| Gini: ∑ j = 1 k p j ∗ ( 1 − p j ) = 1 − ∑ j = 1 k p j 2 \sum_{j=1}^k{p_j*(1-p_j)}=1-\sum_{j=1}^k{p_j^2} ∑j=1kpj∗(1−pj)=1−∑j=1kpj2 | CART | |
| 错分率: 1 − m a x j ( p j ) . 1−max_j(p_j). 1−maxj(pj). |
另一种方法:The Twoing Rule
另一种分类树的分裂方法是“the Twoing Rule”. 与上述的不纯度度量公式不同。
直觉上看,在两个子节点的类别的分布应该尽可能的不同,并且落到子节点中的数据占比应该比较均衡。
The twoing rule: 对于节点 t, 选择一个分裂是使下面值最大的情况:
P R P L 4 ∗ [ ∑ j = 1 k ∣ P ( j ∣ t L ) − P ( j ∣ t R ) ∣ ] 2 \frac{P_RP_L}{4}*[ \sum_{j=1}^k{ |P(j|t_L)-P(j|t_R)| ]^2} 4PRPL∗[∑j=1k∣P(j∣tL)−P(j∣tR)∣]2
当我们把一个节点分裂成两个子节点时,我们希望每个分类的后验概率尽可能的不同。如果差异达到最大,则每个分类都是趋于更纯的。
如果每个子节点分类的后验概率与父节点几本一致,说明子节点的划分并没有使得纯度比父节点更好,因此不是一个好的划分。
总的来说,我们既可以用划分优度也可以用twoing rule方法,在一个节点处,我们可以使用所有的方法,然后选择最好的。
10.3 每个节点下分类的后验概率估计
不纯度的测度是关于k个分类先验概率的函数,这一节,我们要回答如何估计先验概率。
我们先来定义:
- 样本个数为N,样本的有K个分类, N j N_j Nj 是属于j类的样本个数,其中, 1≤j≤K. 如果把所有的 N j N_j Nj加起来,将得到N。
- 对于节点t,t中的样本个数为 N(t),其中,属于j类的样本数为 N j N_j Nj
于是,对于节点t,如果把所有的分类加起来,我们得到:
∑ j = i k N j ( t ) = N ( t ) \sum_{j=i}^k{N_j(t)}=N(t) ∑j=ikNj(t)=N(t)
并且,对于分类j,如果我们把左右子节点的样本数加起来,应该等于父节点的样本数:
N j ( t L ) + N j ( t R ) = N j ( t ) N_j(t_L)+N_j(t_R)=N_j(t) Nj(tL)+Nj(tR)=Nj(t)
接下来我们定义类的先验概率为 π j \pi_j πj. 此先验概率通常通过计算数据中没个分类的占比得到。举例,如果我们想知道类别1的先验概率,我们只需要简单的计算属于类1的数量占总体数量的百分比, N j / N N_j/N Nj/N. 这个比例又叫做类的经验频率。
上述数计算先验概率的一种方式,有时也可能是预先给定的。比如说,在医疗的例子中,研究者收集患有某一疾病的病人了大量的数据。在收集数据中,患有某一疾病的样本比例可能远高于总体的实际比例。这种情况下,就不太适合使用实际数据计算得到的经验频率。但如果数据是总体中的随机样本,则是可行的。
j 类样本属于节点 t 的条件概率估计为, p ( t ∣ j ) = N j ( t ) / N j p(t|j)=N_j(t)/N_j p(t∣j)=Nj(t)/Nj
显然,
N j ( t L ∣ j ) + N j ( t R ∣ j ) = N j ( t ∣ j ) N_j(t_L|j)+N_j(t_R|j)=N_j(t|j) Nj(tL∣j)+Nj(tR∣j)=Nj(t∣j)
假设我们知道如何得到 p ( t ∣ j ) p(t|j) p(t∣j),我们将得到类别 j 和 节点 t 的联合概率:
p ( j , t ) = π j p ( t ∣ j ) = π j N j ( t ) / N j p(j,t)=\pi_j p(t|j)=\pi_j N_j(t) / N_j p(j,t)=πjp(t∣j)=πjNj(t)/Nj
那么在节点t下的样本的概率为:
p ( t ) = ∑ j = 1 k p ( j , t ) = ∑ j = 1 k π j N j ( t ) / N j p(t)=\sum_{j=1}^k{p(j,t)}= \sum_{j=1}^{k}{\pi_j N_j(t) / N_j} p(t)=∑j=1kp(j,t)=∑j=1kπjNj(t)/Nj
现在我们就需要知道如何计算 p(j|t) 了,即节点t下的一个样本属于 j类的条件概率:(注意,此处的条件概率是翻转的,不是p(t|j) )
p ( j ∣ t ) = p ( j , t ) / p ( t ) p(j|t)=p(j,t)/p(t) p(j∣t)=p(j,t)/p(t)
.
决定节点所属分类的规则
假设我们已经构建了一个树,那么这个决策树是如何对新的样本点进行分类点呢,步骤如下:
我们先让样本点根据决策树的规则判断该点会落到哪个叶节点(终节点)。叶节点的类就会赋给这个新的样本点。所有落在一个叶几点的样本点都会被赋予同一个类,这点有点像 k-means 和 其他原型方法。
那么,构建决策树的时候是如何确定一个叶节点(终节点)的类别的呢,步骤如下:
如果我们用0-1损失,那么类的确定规则会很像k均值-我们选择叶节点样本中,出现频次最多的类或者具有最大后验概率的类作为该节点的类:
k ( t ) = a r g m a x P ( j ∣ t ) k(t)= argmax P(j|t) k(t)=argmaxP(j∣t)
假设我们已经有了一个树,而且没个叶节点上也都赋予了分类。现在我们就需要估计这个树的分类错误率了。 在这个例子中,我们需要介绍错分概率的再代入估计 r(t),给定一个落到节点t 的样本,则:
r ( t ) = 1 − m a x p ( j ∣ t ) = 1 − p ( k ( t ) ∣ t ) r(t)=1− max p(j|t)=1−p(k(t)|t) r(t)=1−maxp(j∣t)=1−p(k(t)∣t)
定义 R ( t ) = r ( t ) p ( t ) R(t)=r(t)p(t) R(t)=r(t)p(t),则全体错分概率的再代入估计 R(T)为
R ( T ) = ∑ t ∈ T ′ R ( t ) R(T)=\sum_{t∈T'}{R(t)} R(T)=∑t∈T′R(t)
接下来,我们要花点时间证明如果我们把节点拆分成子节点,那么错分率一定是又提升的。换句话说,如果用再代入估计计算错误率,那么节点的拆分越多,错误率越小。这就导致了再代入误差的一个问题:偏向更大的树。
证明,对于任何节点t,拆分成子节点 t l 和 t R t_l 和 t_R tl和tR 后,均有
R(t)≥R(tL)+R(tR)
10.4 例子(略)
10.5 树结构方法的优点
- 如同我们多次提到的,树结构的方法能以简单的方式处理分类变量和定序变量;
- 分类树有时能够自动的分步骤的进行筛选变量和降低复杂度
- 分类树对于测试的样本点提供了错分类估计
- 分类树对于有序变量的单调变换是不变的。分类树的划分是根据阈值,而单调变换并不改变划分节点的阈值
- 分类树对于异常值和误分类点相对稳健。因为除了数据本身,并不需要计算如平均值等其他指标
- 分类树很容易解释, 特别是在医学领域的应用
10.6 变量合并
目前为止,我们假设分类树只是平行坐标轴地对空间进行划分。对于这样严格地划分,会带来什么结果呢?
让我们来看一下下面这个例子:
如图中所示,我们可能更想要把所有的点按照对角线划分成两类。平行于坐标轴的划分对于这个数据集似乎并没那么有效,还需要更多的步骤去划分。
而且对于分类树的延伸方法也是有许多的,比如并不是按照每个独立变量阈值逐一去划分的线性判别分类(划分一次就使用了样本点的所有信息)。
再或者说,我们用更复杂的问题,如,线性变量的线性组合 (显然增加了计算量):
∑ a j x j < = c ? \sum{a_jx_j}<= c ? ∑ajxj<=c?
研究似乎表明,使用更灵活(复杂)的问题即使没有使结果变坏,也往往不会导致明显更好的分类结果。而且,更灵活的问题更容易导致过拟合问题。
并且,似乎使用正确规模的分类树 相比于 在各自节点上划分的好坏 更重要。
10.7 缺失变量
在一些训练样本中,有些变量可能会有缺失值。测试样本中可能也会有。决策树有个很好的办法处理缺失值——替代分裂(surrogate splits)。
假设对于节点t ,最优的划分是t,该划分用到了 X m X_m Xm变量。那么如果这个变量缺失了怎么办。
分类树将会通过找到一个替代分裂点处理这个问题。通过另一个变量找到另一个划分。遍历所有变量,找到最接近最优划分的替代。如果替代划分同样存在缺失值,那么继续找次优的代替分裂,以此类推。
当搜寻代替分裂时,需要注意一个事项。分类树并不是根据分类优度的测量而找到第二个最好的划分,而是找到尽量接近最优划分结果的代替。“此处接近,个人理解为是结构上的接近”。
下一节:第10章-基于树的方法(2)-树的剪枝