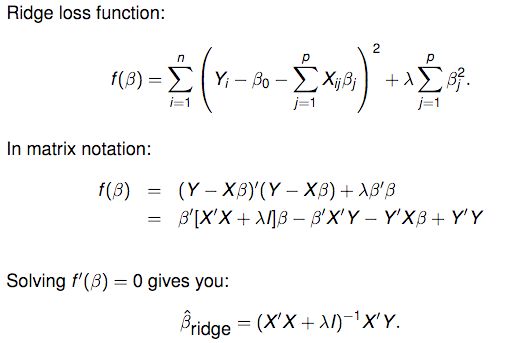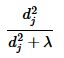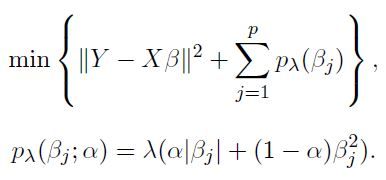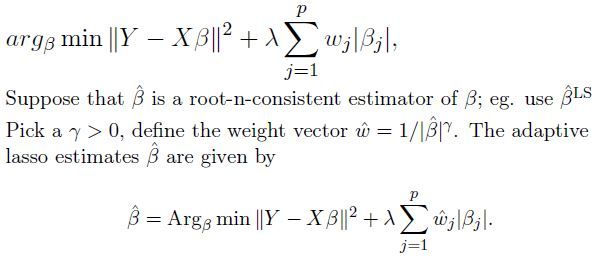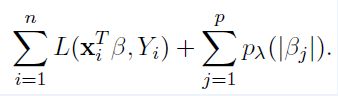第4章-模型中特征子集的选择
原文参考:
https://onlinecourses.science.psu.edu/stat857/node/137
扩展参考:
http://sites.stat.psu.edu/~jiali/course/stat597e/notes2/lreg.pdf
https://etd.ohiolink.edu/!etd.send_file?accession=case1300817082&disposition=inline
田茂再老师上课内容;
http://blog.csdn.net/zouxy09/article/details/24971995/
高维复杂数据分析已经变得越来越常见,并且也越来越重要。它给当代统计学带来了很多问题,样本增加,维度以指数的速度增加。
“Statistical accuracy, model interpretability and computational complexity are three important pillars of any statistical procedure.”
— Fan and Lv (2010).
维度的复杂性加大了计算的复杂性,也影响着模型的可解释性,如何解决这些问题?—这就引出了特征子集的选择问题(subset selection).
子集的选择,实质就是对变量进行选择。不同特征(变量)的组合构成了模型的全部集合,而最优的模型就存在于我们要找到的特征子集中。
寻找特征(变量)时,该是以改善、提高模型预测效果为目标的。
当然,还需要考虑模型的过拟合的问题,所以,变量选择的过程同样要遵循—balance between bias and variance.
一,经典统计方法:
(1)基于假设,通过系数t、f值的判断
Two ways: forward selection and backward elimination.
(2)基于规则的判断,通过结合AIC、BIC、LRT、拟合优度等准则来进行变量的筛选
缺点:无法处理高维数据,且该方法不稳健。这种方法筛选变量的时候,需要遍历2^p个候选模型去进行两两比较。
(3) Resampling,抽样结合上述2中方法
在不同变量选择所形成的不同模型之间的比较阶段,一般是采用逐步回归,加上上述三种方法进行的。
三,正则化方法:
为了克服传统经典方法的缺点,对应高维数据的变量筛选出现了一些新的技术—正则化(Regularization)。
正则化项是在机器学习中经常使用的方法,谈起正则化项,应该先从经验风险开始说起:
机器学习本质上是一种对问题真实模型的逼近。估计的模型与真实模型之间的误差的累积,就是“风险".
真实的误差或者说风险是无法得到的,只能去估计,这种使用样本得到的结果与真实结果之间的差值就是,“经验风险”—对风险的估计
以前的机器学习方法,都是把经验风险最小化作为努力的目标,但是后来发现某些准确率100%的模型,其泛化能力可能非常差。
统计学因此引进了 “泛化误差界” 的概念,就是指真实的风险应该有两部分构成,一部分是"经验风险",另一部分是"置信风险"。
置信风险代表了,能够在多大程度上信任分类器在未知样本上的分类结果。显然,第二部分也是无法精确计算的,只能给出区间。这也使得整个误差只能计算上界,而无法计算精确的值。
“置信风险” 与两个量有关,一是样本量,二是分类函数的VC维。显然样本量越大,置信风险越小,而VC维越大置信风险会变大。
泛化误差界的公式为:
R(w)≤Remp(w)+Ф(n/h)
公式中R(w)就是真实风险,Remp(w)就是经验风险,Ф(n/h)就是置信风险。统计学习的目标从经验风险最小化变为了寻求经验风险与置信风险的和最小,即结构风险最小。
正则化是结构风险最小化策略的实现,是在经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化项就越大。
综述,我们有两个大角度来看待变量选择的问题,一个是概率统计的角度(经典统计方法与贝叶斯方法),一个是机器学习中的算法模型的角度(正则化)。
本章主要学习目标:
- 知道如何实现岭回归;
- 知道如何实现LASSO;
知识回顾:
(1) 线性回归
- 线性回归: E(Yj|X)=Xβ;
- 更一般的回归: E(Yj|X)=f(X);
- 最小二乘估计得 β ^ = ( X T X ) − 1 X T Y \hat{β}=(X^TX)^{-1}X^TY β^=(XTX)−1XTY
- 拟合值为 Y ^ = X β ^ = X ( X T X ) − 1 X T Y \hat{Y}=X\hat{β}=X(X^TX)^{-1}X^TY Y^=Xβ^=X(XTX)−1XTY
- 帽子矩阵(hat matrix): X ( X T X ) − 1 X T X(X^TX)^{-1}X^T X(XTX)−1XT
- 几何意义:正交投影

(2) 变量选择
- 对精简模型复杂性的诉求
- 对提高预测精准性的诉求
- 如何确定变量是重要的一个解释就是(Breiman,2001):如果去掉这个变量将严重影响预测的准确性,那么该变量就是重要的
- 建模过程中筛选变量是一个非常复杂的问题,对于一些方法,如似然比检验、F检验、AIC、BIC等,这些指标本身有时会给出相互矛盾的意见
(3) 逐步回归
- 向后剔除法:先选入所有变量,然后逐步提出重要性最低的变量;
- 向前选择法:逐步选入最重要的变量加入到模型中;
- 混合型:结合上述两种
- 前向分段/分步算法(Forward-Stagewise)
(4) 逐步回归的评价
- 无法保证逐步回归选择的变量是稳定的,甚至说是最好的
- 当变量个数大于样本个数时 (p > n), 后向剔除法会变得不可行
- 对于变量选择问题,逐步发只产生一个结果,尽管可能有其他变量子集会产生同样好的回归结果
- 在R中,用step()/regsubsets()方法,很容易能实现逐步回归。然而,对于如何选择一个最优的结果,你必须知道用什么样的推断工具去实现
- Scott Zeger 针对如何错误地选择模型时说过:不要把科学问题转化成计算问题,只知道选择一个最好的AIC、BIC等,而不知道其背后隐藏的科学问题
3.1 岭回归
岭回归的动机:特征变量太多
- 变量个数比观察个数多很多的情况下,如环境污染研究等
- 变量太多时,不加惩罚的拟合模型时,将会导致预测区间很大,最小二乘估计值将不会产生唯一结果
岭回归的动机:病态的X矩阵
- 因为最小二乘估计的解会依赖矩阵 ( X ′ X ) − 1 (X′X)^{-1} (X′X)−1, 如果矩阵X′X 不满秩,即为奇异矩阵,则计算参数β时将会出现问题。
- 在这种情况下,X 中元素的微小波动,都会导致 ( X ′ X ) − 1 (X′X)^{-1} (X′X)−1的剧烈变化
- 最小二乘估计 β L S β_LS βLS 可能对训练集可以得到一个较好的估计,但是对于测试集仍不满足
岭回归:
Hoerl and Kennard (1970) 建议,对潜在不稳定的最小二乘估计
β ^ = ( X ′ X ) − 1 X ′ Y \hat{β}=(X′X)^{-1}X′Y β^=(X′X)−1X′Y
在求逆之前,可以先在矩阵X′X的对角线添加一个很小的常量λ,形成"岭回归"估计
β ^ r i d g e = ( X ′ X + λ I p ) − 1 X ′ Y \hat{β}_{ridge}=(X′X+λI_p)^{-1}X′Y β^ridge=(X′X+λIp)−1X′Y
岭回归在参数的求解过程中加入了一个特别形式的限制,即最小化带有惩罚项的误差平方和:
从上述推倒中,可以看出,β的平方正则化项与岭回归是等价的。
因此,岭回归进一步的限制了参数。在上述公式中,对于f(β)最小化的目标公式不仅仅是残差平方和,还有惩罚项。
等价于,最小化RSS![]() ,同时满足一个条件,即,对于c>0有,
,同时满足一个条件,即,对于c>0有,![]()
这意味着如果 β的求解值很大,那么对应的代价也很大。所以,最终结果倾向于选择较小的或者接近零的 β,以便限制惩罚项具有更小的值。
模型求解的复杂度,也取决于c和λ的值。
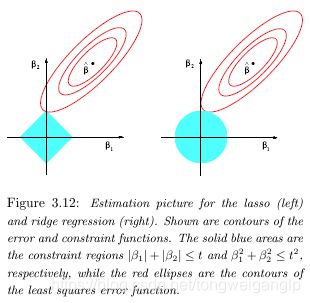
椭圆对应的等高线轮廓代表着残差平方和(RSS):轮廓越小代表着残差平方和越小,在最小二乘估计下,残差平方和最小。
当维度p=2时,岭回归估计受限于条件: ∑ j = 1 p ( β j 2 ) < c \sum_{j=1}^p(β_j^2)<c ∑j=1p(βj2)<c
岭回归中我们试图同时使得椭圆和圆达到最小规模。岭回归估计就是椭圆与圆的交点。
我们要权衡惩项和RSS之间的值,且惩罚项中(λ和c之间是对应的),λ越大(c越小), β j β_j βj 就越接近零。极端情况下,当λ=0时,那么岭回归将退化成普通的线性回归。相反,如果λ接近无穷大那么所有的 β j β_j βj 都接近零。
岭回归估计的特点:
(1) β的最小二乘估计是无偏的,而β的岭回归估计是有偏的。
(2) 对于正交协变量, X ′ X = n I p , β ^ R i d g e = n n + λ β ^ L s X'X=nI_p,\hat{β}_{Ridge}=\frac{n}{n+λ}\hat{β}_{Ls} X′X=nIp,β^Ridge=n+λnβ^Ls
因此,岭回归估计倾向于把参数压缩成0,λ 控制着压缩的程度。
(3) 有效自由度

其中,d是X的奇异值。
对于有效自由度,如果λ=0,我们有p个参数(无惩罚项),即有效自由度为p;如果λ非常大(λ→∞),参数将受很大限制,且有效自由度将变得很小,趋于0.
另一个角度看岭回归的几何解释(选学):
(1) 奇异值分解中, X = U D V T X=UDV^T X=UDVT,其中u是n*p正交矩阵,v是p*p正交矩阵,D是X的奇异值,
( X X X的奇异值为 X T X X^TX XTX的特征根的平方值)
D = d i a g ( d 1 , d 2 , . . . , d p ) , d 1 ≥ d 2 ≥ . . . ≥ d p ≥ 0 D=diag(d_1,d_2,...,d_p),d_1≥d_2≥...≥d_p≥0 D=diag(d1,d2,...,dp),d1≥d2≥...≥dp≥0
(2) 主成分分解中,协方差矩阵S,
S = E ( ( X − E ( X ) ) T ∗ ( X − E ( X ) ) ) S=E((X-E(X))^T*(X-E(X))) S=E((X−E(X))T∗(X−E(X)))
则对于,已经中心化的输入X, S = X T X / N S=X^TX/N S=XTX/N
结合奇异值分解,我们可得:
X T X = V D U T ∗ U D V T = V D 2 V T X^TX=VDU^T *UDV^T =VD^2V^T XTX=VDUT∗UDVT=VD2VT
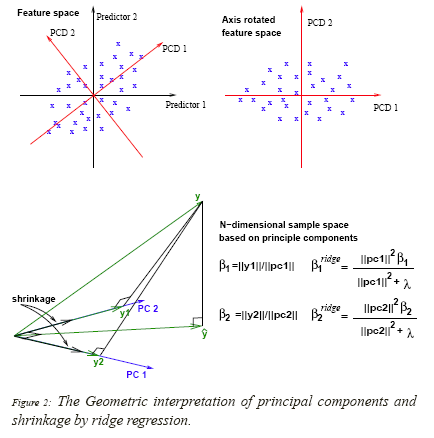
(3) 岭回归几何含义
首先,输入X要中心化 (目的:去掉常数项 β 0 β_0 β0);
接下来,考虑相应变量:

其中, u j u_j uj是的X的标准化后的主成分
(主成分实质上是变换后的另一组正交基/坐标)
我们可得结论:
(1) 岭回归是对主成分形成的正交基进行维度压缩的;
(2) 主成分中的方差越小,对应的坐标就越会被压缩;
(3) 如果我们不再用X作为输入,而是新的输入矩阵 X ^ = U D \hat{X}=UD X^=UD(注X的完整的奇异值分解为 X = U D V T X=UDV^T X=UDVT),则我们得到
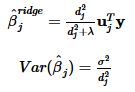
其中, σ 2 σ^2 σ2是表示线性模型中的残差项的平方
我们可以看出,λ越大,在 u j u_j uj上的投影被压缩的也越大,所以形成了上述结论中的第二点。
3.2 LASSO
岭回归的结果可能仍然很难解释,因为β只是接近零,而不没有被压缩等于零。那么如果我们把损失方差中的限制条件变为从二范式变为一范式,会发生什么呢?
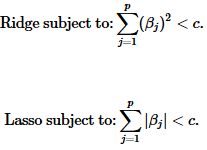
这是一个微小的,但却十分重要的变化。一些系数会被完全压缩为零值。
1996年,Robert Tibshirani 发表了这项变量压缩的技术,该算法全名为,The least absolute shrinkage and selection operator, 简称 lasso。
lasso是用一范式进行限制压缩的,所以在限制阈中,是存在"直角"的。以二维情况下为例,值域与限制阈相交的点被压缩到了坐标轴上(意味着与坐标轴垂直的维度上的值可能被压缩为零了)。
lasso实际上是一种"软阈值"方法,当参数变化时,估计参数的变化路径是连续的趋于零的。
与岭回归不同,因为其在Y轴是非线性的,所以没有解析解。但是可以用2003年,Efron发明的最小角向量算法(LARS)进行求解。
3.3 岭回归和LASSO的比较
用下面数据举例说明:
PGA data (Anderson, Sweeney and Williams, 2003)
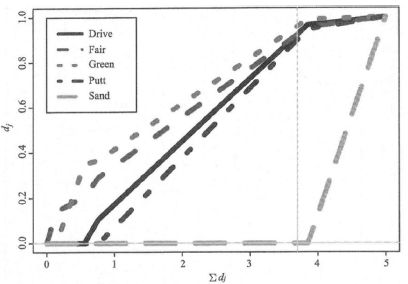
运用ten fold cross validation生成下图
由上图可知,随着Σd=M的不同,权重d也在变化,M=p=5时,d=1相当于权重没有影响,所以,一般选取M≤p即可。而如果M=3~4之间(图中竖线位置),则Sand这个变量的d=0,这个维度就被剔除了。
(2) LASSO and Bridge Regression
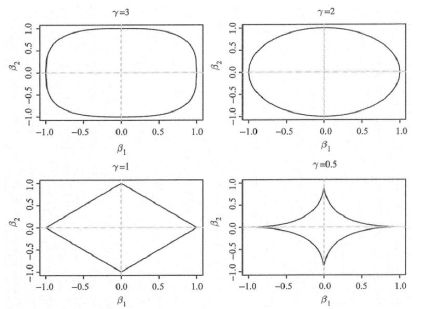
仍以PGA数据举例,并通过ten fold cross validation生成
2维下,桥回归,不同r对应的可行域及beta值如下
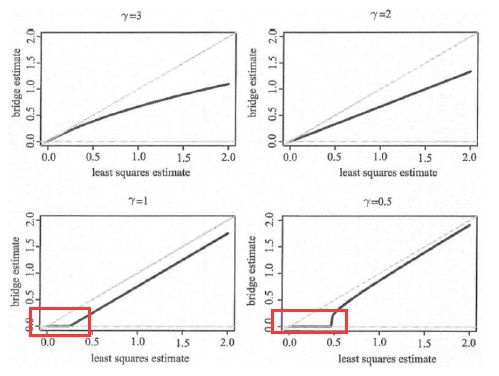
下图是最小二乘的beta系数与桥回归beta系数之间的对应关系
可见只有r≤1时,压缩效果才好,“encourages sparsity”很小的beta值对应的变量会被剔除掉。
3.4 其他方法
(1) smoothly clipped absolute deviation (SCAD)
–(Fan and Li, 2001)
(2) elastic net-(Zou and Hastie, 2004)
LASSO的局限:
- p > n, lasso selects at most n variables;
- Group variable, select only one;
- n > p, if there are high correlations between predictors, the prediction performance of Lasso is dominated by ridge regression (Tibshirani, 1996).
elastic net 结合了lasso与岭回归的惩罚项(正则项)
(3) Adaptive LASSO–(Zou, 2006)
对LASSO的惩罚加权
Motivation:
- The lasso shrinkage produces biased estimates for the large coefficients;
- The optimal for prediction gives inconsistent variable selection results.
(4) 更一般的方法
除了改变惩罚项,结合不同的模型,选择不同的损失函数也是可以的。
比如说,结合分位回归:
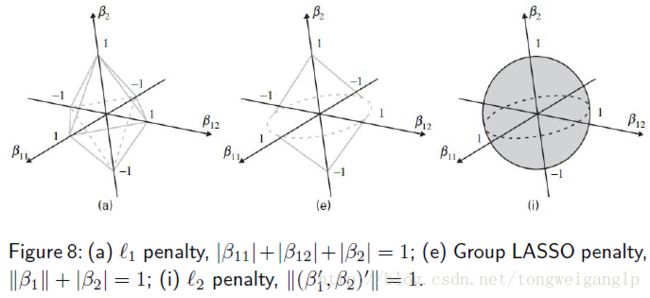
(5) 组变量筛选(Group variable selection)
当模型中的变量有名义变量或有序变量的时候(需要虚拟化的时候),变量选择会出现一类问题。如,变量间有交互作用的时候,变量虚拟化后,以不同的类别值作为基组(即,虚拟变量均为0时对应的类别)时得到的beta值也会有很大不同。
以上述问题为背景,引出了组变量的筛选:
Group LASSO (Yuan & Lin, 2006)
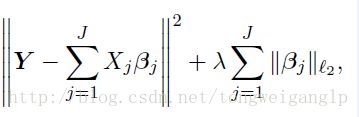
与LASSO的区别是,事先分组,J是组数,此处的beta值也是向量,即该组对应的向量值。
(6) 继承原则
其他情况下,当模型中出现交互作用时,如,x1,x2的beta系数已压缩成0, 但是其交互作用x1*x2却是显著的。
此时,就要考虑到继承性问题。
3.5 结构风险最小化策略
我们衍生地讲一下更一般的结构风险最小化策略。机器学习的大部分带参模型都基本都是这种策略形式:定义不同的"损失函数+正则化项"。
其中,对于损失函数
如果是Square loss,那就是最小二乘了;
如果是Hinge Loss,那就是SVM了;
如果是exp-Loss,那就是Boosting了;
如果是log-Loss,那就是Logistic Regression了;等等。
接着对于正则化项,也有很多种情况:零范数、一范数、二范数、迹范数、Frobenius范数和核范数等等。
L0范数是指向量中非0的元素的个数。L1范数是指向量中各个元素绝对值之和。L2范数即平凡平方和。核范数(Nuclear Norm)||W||*是指矩阵奇异值的和,用来约束Low-Rank(低秩)。
如果X是一个m行n列的数值矩阵,rank(X)是X的秩,假如rank (X)远小于m和n,则我们称X是低秩矩阵。低秩矩阵每行或每列都可以用其他的行或列线性表出,可见它包含大量的冗余信息。利用这种冗余信息,可以对缺失数据进行恢复,也可以对数据进行特征提取。
正则化项除了有上述所说的不同的范数特征外,一般都带有一个参数—叫hyper-parameters(超参),形如λΩ(w)。它的取值很大时候会决定我们的模型的性能,主要是平衡loss和规则项这两项的。
确定超参λ,一种最常见的方法就是交叉验证Cross validation了。先把我们的训练数据库分成几份,然后取一部分做训练集,一部分做测试集,然后选择不同的λ用这个训练集来训练N个模型,然后用这个测试集来测试我们的模型,取N模型里面的测试误差最小对应的λ来作为我们最终的λ。