第10章-基于树的方法(2)-树的剪枝
10.8 通过剪枝得到最优规模的树
之前我们讨论的都是如何生成树,接下来我们要讲解的是如何进行剪枝。
我们令一个树 T 的误分类误差的期望为 R ∗ ( T ) R^*(T) R∗(T).
回想一下,我们是用再代入误差估计,估计的 R ∗ ( T ) R^*(T) R∗(T),即
R ( T ) = ∑ t ∈ T ′ R ( t ) = ∑ t ∈ T ′ p ( t ) r ( t ) R(T)=\sum_{t∈T'}{R(t)}=\sum_{t∈T'}{p(t)r(t)} R(T)=∑t∈T′R(t)=∑t∈T′p(t)r(t)
再来想一下,10.3中所讲的,r(t)是叶节点t的误分类概率,等于
1-‘基于训练集得到的叶节点t的频率最大的类别点对应的概率’, 即
r ( t ) = 1 − m a x p ( j ∣ t ) = 1 − p ( k ( t ) ∣ t ) r(t)=1− max p(j|t)=1−p(k(t)|t) r(t)=1−maxp(j∣t)=1−p(k(t)∣t)
对于整个树,对叶节点的误分类比例进行加权累计求和,就得到了总的误分类概率。
并且,在10.3中,我们提到过,再代入误差是有趋于更小的,即树倾向生成更大的规模。我们证明了,父节点的误分类概率一定大于等于子节点误分类概率加权求和。
R ( t ) ≥ R ( t L ) + R ( t R ) R(t)≥R(t_L)+R(t_R) R(t)≥R(tL)+R(tR)
以上说明,如果我们用再代入误差最小化为策略时,我们总是倾向于选择更大的树,且无法解决减轻过拟合的影响。
(例子 略)
10.8.1 剪枝的预备知识
首先,我们先要生成最大的树,用 T m a x T_{max} Tmax来表示。
其次,设置停止生成树的阈值并不是那么重要。因为,只要树足够大,何时停止生成树影响不大。最后,树也都会在剪枝过程中被修减。下面列出几种决定何时停止生成树的方法:
- 一直生成树,直到所有的叶节点都是"纯的"(只属于一类)
- 一直生成树,直到所有的叶节点之和都不超过给定的阈值
- 只要树足够大,原始树的大小就会变得不那么重要
以上,重点就是要确保剪枝之前树要生成的足够大。
最后,我们需要预先进行一些定义:
- Descendant: 如果一个节点 t′ 可以从一个节点 t 沿着一个连续路径向下派生出来,我们就说,t’是t的派生节点(Descendant)
- Ancestor: 在1中的情况中,反过来说,t 是 t’的Ancestor节点
- A branch T t T_t Tt: 在一个树T 中,以一个节点t(t∈T)为根节点衍生出来的所有子(叶)节点,包括t点本身,构成了 T t T_t Tt
- 从树T 中剪枝去掉 T t T_t Tt,意味着从T中去掉t节点以及t节点派生出来的所有节点,可用 T − T t T−T_t T−Tt表示。
- 如果T′ 是树T 已经剪枝成功后的状态,那么T’ 被称为T的剪枝后的子树,且 T ′ < T T'<T T′<T
即使对于适中规模的树来说,子树的数量都是非常巨大的。因此,我们无法穷尽遍历所有子树找到最优的情况。而且,我们通常也没有独立的测试集为有偏的选择提供服务。
我们需要更聪明的办法,这个办法需要满足以下两点:
- 某种程度上看,子树要是最优的
- 且,最优子树的搜索,计算量要保证简单易行
10.8.2 最小代价-复杂度的剪枝
如之前讨论的,再代入误差 R(T) 并不是一个很好选择子树的度量方式,因为它会倾向选择更大的树。我们需要加入对复杂度的惩罚,惩罚项要倾向于更小的树,以此来平衡再代入误差 R(T)。
代价-复杂度的定义:
对于任一子树 T < T m a x T<T_{max} T<Tmax , 定义树的复杂度为 ∣ T ∗ ∣ |T^*| ∣T∗∣, 表示树的叶节点(终节点)的个数。定义实数 α≥0,被称作复杂度参数 ,则定义代价-复杂度 R α ( T ) R_α(T) Rα(T)为
R α ( T ) = R ( T ) + α ∣ T ∗ ∣ R_α(T)=R(T)+α|T^*| Rα(T)=R(T)+α∣T∗∣
叶节点越多,复杂度也就越大,因为我们把空间划分成子区域的方式会有更多,所以,会有更大的可能性更适合训练集的数据。除了复杂度,树的规模也是非常重要的。而这些问题都转化为用复杂度参数 α 来进行调整了。
最后,我们就说用上述的代价复杂度公式进行树的剪枝的。当 α=0 时,复杂度相当于被去掉,退化成再代入误差。所以,公式会选择生成最大规模的树。当 α 接近无穷大时,树的规模将为1,只有单一根节点。
通常,如果预先给定α 后,就能够找到子树T(α),使得代价复杂度 Rα(T) 最小。
R α ( T ( α ) ) = m i n ( R α ( T ) ) , T ≤ T m a x R_α(T(α))=min(R_α(T)), T≤T_{max} Rα(T(α))=min(Rα(T)),T≤Tmax
那么,对于任意一个 α,最小化子树总是可解的。因为只有有限多个子树。
两个问题:
- 存在一个唯一的子树 T < T m a x T<T_{max} T<Tmax,满足 R α ( T ) R_α(T) Rα(T) 最小么?
- 在最小化子树的序列中,T1,T2,⋯每个子树能否通过对上一个子树剪枝得到,即,这些子树是嵌套的么?
如果最优的子树都是嵌套的,那么计算量将会大幅下降。我们先找到 T 1 T_1 T1,然后找 T 2 T_2 T2时,不需要再从头开始,而是直接从 T 1 T_1 T1开始(因为T2是T1的子树,是嵌套的)。随着 α 的增加,我们将对越来越小的树进行剪枝。
定义:对于参数α,最优最小树 T α T_α Tα:
- R α ( T ( α ) ) = m i n ( R α ( T ) ) , T ≤ T m a x R_α(T(α))=min(R_α(T)), T≤T_{max} Rα(T(α))=min(Rα(T)),T≤Tmax
- 如果 R α ( T ) = R α ( T ( α ) ) R_α(T)=R_α(T(α)) Rα(T)=Rα(T(α)),那么 $ T(α)≤T$,即,如果对于同样的 α , 存在其他的树的代价复杂度同样也达到最小,那么其他树的规模一定是小于等于 T ( α ) T(α) T(α).
根据上述定义,如果T(α)存在,那么一定是唯一的。之前我们也讨论过最小子树总是存在的,因为只有有限个子树。更近一步,我们可以证明最小子树总是存在的。这点是很重要的,因为一个树比另一个树小,说明它是是嵌套在大一点的树中的。
剪枝的开始点不是 T m a x T_{max} Tmax(所有叶节点都是纯的), 而是 T 1 = T ( 0 ) T_1=T(0) T1=T(0), T 1 T_1 T1 是 T m a x T_{max} Tmax的最小子树(最小损失复杂度),且满足:
R ( T 1 ) = R ( T ( 0 ) ) = R ( T m a x ) R(T_1)=R(T(0))=R(T_{max}) R(T1)=R(T(0))=R(Tmax)
得到 T 1 T_1 T1的步骤如下:
首先,先来看最大树 T m a x T_{max} Tmax,然后从同一个父节点划分出两个叶节点 t L , t R t_L,t_R tL,tR,如果这两个叶节点的再代入误差和与父节点的再代入误差相等,那么需要把这两个节点剪掉。即,当 R ( t ) = R ( t L ) + R ( t R ) R(t)=R(t_L)+R(t_R) R(t)=R(tL)+R(tR)时,剪去左右子节点。
这个过程是递归实现的。当我们把一对子节点剪掉时,树的规模缩小了一点。然后,根据这个更小规模的树,同样进行递归,直到不满足等式为止。这样生成得到的树,就是从 T 1 T_1 T1得到的。
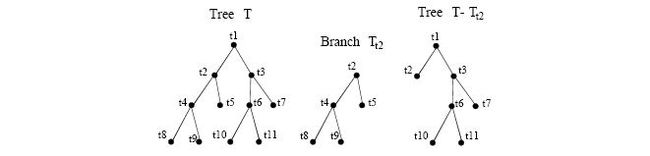
我们来看一个例子---如何得到 T m a x T_{max} Tmax
(图中,可以剪枝掉 t 8 , t 9 t_8,t_9 t8,t9,所以从 T 1 T_1 T1得到的剪枝应该树不包含这两个子节点的。满足: R ( T 1 ) = R ( T ( 0 ) ) = R ( T m a x ) R(T_1)=R(T(0))=R(T_{max}) R(T1)=R(T(0))=R(Tmax),且小于等于 T m a x T_{max} Tmax.)
我们定义 T t T_t Tt是以t为根节点的派生出来的树。对于 T t T_t Tt,我们定义这个树的再代入误差, R ( T t ) R(T_t) R(Tt),为:
R ( T t ) = ∑ t ′ ∈ T t ′ R ( t ′ ) R(T_t)=\sum_{t' ∈ T_t'}{R(t')} R(Tt)=∑t′∈Tt′R(t′)
其中, T t ′ T_t' Tt′ 为树的所有叶节点的集合。
可以证明,如果节点t 不是树 T 1 T_1 T1 叶节点,是中间节点,那么节点t的再代入误差一定大于该节点下的树的再代入误差,即 R ( t ) > R ( T t ) R(t)>R(T_t) R(t)>R(Tt)。如果我们把节点t 下的树剪掉,那么总体的再代入误差一定是增加的。
Weakest-Link Cutting
weakest link cutting 方法不仅能找到下一个最优子树对应的复杂度参数 α 的值,还能确定这个最优子树。
对于任意的t∈T1, 定义 Rα(t)=R(t)+α*1
对于任意的以t节点衍生出的分支 Tt, 定义 Rα(Tt)=R(Tt)+α|T̃t|
则当α=0时, R 0 ( T t ) < T 0 ( t ) R_0(T_t)<T_0(t) R0(Tt)<T0(t),当α保持足够小时,不等式都会成立。
当逐渐增大α时,因为Rα(Tt)的增速会更快,当α达到一个特定值,我们将会有等式 R α ( T t ) = R α ( t ) R_α(T_t)=R_α(t) Rα(Tt)=Rα(t) .
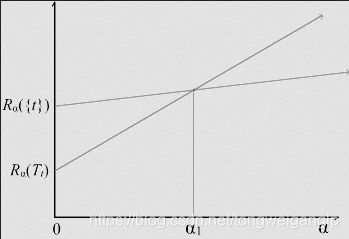
如上图,当 α 继续增加,则不等式将出现反转,得到 Rα(Tt)>Rα(t)。
对于一些节点t 可能比其它节点更容易达到等式(所满足的条件)。以最小 α 值达到等式所满足条件的节点-被称为 weakest link. 可能会出现若干点同时满足等式得到 weakest link 节点的情况.
解不等式 R α ( T t ) < R α ( t ) R_α(T_t)<R_α(t) Rα(Tt)<Rα(t),得到
α < R ( t ) − R ( T t ) T ~ t − 1 α < \frac{R(t)-R(T_t)}{T̃_t-1} α<T~t−1R(t)−R(Tt)
不等式右边是再代入误差的差值与复杂度差值的比值,因为分子分母均为正,所以值是正数。
定义函数 g 1 ( t ) , t ∈ T 1 g_1(t),t∈T_1 g1(t),t∈T1
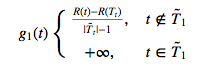
定义分支 T 1 T_1 T1 中的最弱链节点 t ¯ 1 t¯_1 t¯1 为 g 1 ( t ) g_1(t) g1(t) 的最小值.
![]()
然后令 α 2 = g 1 ( t ¯ 1 ) α_2=g_1(t¯_1) α2=g1(t¯1)
为了根据 $α_2 $得到最优子树,可以简单的移除掉 t ¯ 1 t¯_1 t¯1 分支.如果有若干节点都达到了使 g1(t) 最小, 我们就把这些节点衍生出的子树都剪掉。
α2 是 α1=0 之后的第一个值,使得最优树比 T 1 T_1 T1规模要小. 对于所有满足 α1≤α<α2 的α,最优树都是 T 1 T_1 T1.
令 T 2 = T 1 − T t ¯ 1 T_2=T_1-Tt¯_1 T2=T1−Tt¯1
重复之前的步骤,从 T2 而不是 T1 作为搜索最优树的开始,找到T2中的最弱链节点,剪掉对应的分支得到下一个最优子树。(递归思想)
所需计算
计算的时候,我们需要在每个节点存储一些值:
- R(t) -节点 t 的再代入误差. 只需计算一次.
- R(Tt)-节点 t 衍生的分支对应的再代入误差. 剪枝后需要重新计算
- |Tt| -节点 t 衍生分支下的叶节点数量. 剪枝后需要重新计算
(上述三个值要如何计算-略)
α k α_k αk 的法则
法则认为,对于递增序列 {αk} , αk<αk+1,k≥1,where α1=0
对于任意 k≥1,αk≤α<αk+1,最优树都满足 T(α)=T(αk)=Tk ,与 αk 下得到的最优子树一致。这就说明,最优子树Tk在αk≤α<αk+1时,对于连续的 α 来说,最优子树都是Tk。
在剪枝的初始步骤中,算法倾向于快速的剪去包含许多叶节点的大分支。然后,剪枝速度会随着树的变小而越来越慢,算法倾向于剪掉更少的点。
10.8.3 最优的剪枝后的子树
有两种方法来选择最优的剪枝后的子树:
(1) 使用测试集
如果我们有一个很大的测试集,我们就可以用测试集来计算所有子树的误差,以此找出使得误差率最小的子树。然而,实际中,我们很少能有一个很大的测试集。即使我们有一个很大的测试集,我们宁愿用它来训练一个更好的树,而不是去测试。当样本缺少时,我们更不愿意拿太多的数据去进行测试。
(2) 使用交叉验证
当决策树的生成结果都是不稳定的,又如何进行交叉验证呢?如果训练数据变动一点,则结果可能导致结果变化很大。因此,交叉验证中的树与用全部数据生成的树可能很难相匹配。
然而,尽管我们说树的结果本身可能是不稳定的,但是这不意味着每个树的分类结果是不稳定的。我们可能最后有两棵看似不同的树,但是它们对于分类的结果却是相似的。
决策树的关键策略是选择正确的复杂参数α. 决策树试图找到最优的参数,而并不是评判哪个树最优。
基于交叉验证的剪枝
让我们考虑下 V折交叉验证
我们将原始训练样本L,随机分成V份子样本。 L v , v = 1 , . . . , V L_v, v=1,...,V Lv,v=1,...,V. 同时,定义每一折训练样本 L ( v ) = L − L v L^{(v)}=L-L_v L(v)=L−Lv.
然后,我们定义基于原始数据集生成的树为 T m a x T_{max} Tmax, 那么我们重复每一折交叉验证的步骤,得到基于 L ( v ) L^{(v)} L(v) 的 T m a x ( v ) T_{max}^{(v)} Tmax(v).
对于每一个复杂度参数 α ,我们令 T ( v ) T^{(v)} T(v) 是 L ( v ) ( α ) L^{(v)}(α) L(v)(α) 下对应的最优代价复杂度子树 .
对于每个最大树,我们得到严格递增的 α 值,α1<α2<α3⋯<αk<⋯
然后,基于 α 找到最小代价复杂度。如序列中对于 αk≤αk+1,αk 的最优子树就是 α 的子树。
树T(α) 的交叉验证的错误率通过下式计算:

分母:每一个Lv样本中的个数
分子:每一个Lv样本中的错分类个数
T(v)(α) 是基于Lv样本中的树 T(v)max 剪枝后的最优子树。
尽管 α 是连续的,但基于总体样本L,有有限多个最小代价复杂度的树. 考虑每个基于样本L 剪枝后的子树,令 T k = T ( α k ) T_k=T(α_k) Tk=T(αk).
为了计算 T k T_k Tk的交叉验证错误率,令 α ′ k = ( α k ∗ α ′ k + 1 ) 0.5 α′_k=(αk*α′_{k+1})^{0.5} α′k=(αk∗α′k+1)0.5.(这个公式没太懂)
得到
R C V ( T k ) = R C V ( T ( α ′ k ) ) R^{CV}(T_k)=R^{CV}(T(α′k)) RCV(Tk)=RCV(T(α′k))
根据上述公式,得到最小值的 T k T_k Tk将被选中。
(10.8.4将与10.11-10.13写到一起)
10.9 R Scripts
1) 获取数据
糖尿病数据,数据集是从 UCI 机器学习 数据库获取的,地址:
http://archive.ics.uci.edu/ml/datasets/Pima+Indians+Diabetes.
- 样本中有768个数据
- 8个数值型变量
- 2种类别:是否有糖尿病标记
把数据加载到R中,如下:
其中,RawData 的最后一列是因变量(响应变量) ,其余列均是自变量。
# set the working directory
setwd("C:/STAT 897D data mining")
# comma delimited data and no header for each variable
RawData <- read.table("diabetes.data",sep = ",",header=FALSE)
responseY <- as.matrix(RawData[,dim(RawData)[2]])
predictorX <- as.matrix(RawData[,1:(dim(RawData)[2]-1)])
data.train <- as.data.frame(cbind(responseY, predictorX))
names(data.train) <- c("Y", "X1", "X2", "X3", "X4", "X5", "X6", "X7", "X8")
2)分类与回归树
构建分类树模型分为两步:生成树以及剪枝。
2.1) 生成树
rpart(formula, method=“class”) 表示响应变量是分类型的;
rpart(formula, method=“anova”) 表示响应变量是连续数值型的;
library(rpart)
set.seed(19)
model.tree <- rpart(Y ~ X1 + X2 + X3 + X4 + X5 + X6 + X7 + X8, data.train, method="class")
下面代码可以画出树,plot(result, uniform=TRUE) 画出树的节点,且是垂直等距的;然后 text(result, use.n=TRUE) 是把决策规则画在节点上。
plot(model.tree, uniform=T)
text(model.tree, use.n=T)
上图中,显示了分类树的每个节点上的预测条件和决策的阈值,并在每个叶节点上显示了样本不同分类的数量。符号’/’ 左侧显示的是 0-类 样本点数量,右侧显示的是1-类 样本点数量。
在每个节点处,如果判断条件是真,则从左侧分支向下延伸,如果为假,则从右侧分支向下延伸。rpart 包的函数画出的树的规则是:让左侧分支属于0-类的响应变量的比例要高于右侧分支。所以,一些决策规则包含“小于”另一些会包含“大于等于”的符号。相比之下,tree 包的函数画出来的树中,所有的决策规则都是“小于”,所以有的分支下对应的0-类响应变量的比例高,有的则小。
2.2) 剪枝
为了避免过拟合进而得到最优规模的决策树,可以使用 rpart 包生成的cptable 中的元素。
model.tree$cptable
结果如下:
cptable 提供了对于所有适合的模型的一个概要。数据从最小的树(没有分裂),一直到最大的树。
cp : 表示复杂度参数;
nsplit:表示分裂节点的数量;
xerror:表示交叉验证得到的错误率;
xstd:表示交叉验证得到的错误率的标准差;
通常,我们选取最小xerror值对应的树。
通过下面的代码可以自动的获取最优子树:
opt <- model.tree$cptable[which.min(model.tree$cptable[,"xerror"]),"CP"]
opt 存储着最优复杂度参数。然后根据我们选取的这个参数值可以进行剪枝,做法很简单:根据prune函数进行剪枝,该函数把原始为剪枝的树作为第一个参数,把选取的最优复杂度参数作为第二个参数。
model.ptree <- prune(model.tree, cp = opt)
可以用summary() 函数,以获取剪枝后的树的更多信息
上一节:第10章-基于树的方法(1)-生成树
下一节:第10章-基于树的方法(3)-树的改进-集成方法