第2章-回归模型(1)-线性回归模型与估计
简介
最早接触线性回归,是在计量经济学中。最简单最基础的即是一元线性回归模型。通过一元线性回归可以衍生出了许多模型,所以学好一元线性回归是非常有必要的,是目前所有回归模型的基础。即使跳出统计、计量的领域,到了数据挖掘、人工智能的领域,线性回归模型也是打好基础的重中之重。
谈到模型之前,样本数据的类型也是值得探讨的。按照数据截取的方向划分,有三类:
- 横截面数据(cross section data)
- 时间序列(time series)
- 两者混合的面板数据(panel data)也叫纵面数据(longitudinal section data)
不同的数据类型,对应的模型选择也大不相同,比如有专门的时间序列模型参见后续将要写的第二十二章内容,面板数据模型,参见第八章。
线性回归,一般研究的都是横截面数据(简称截面数据),数据挖掘、人工智能重点模型大都也都是选择截面数据。
第二、三、八等章均是主要从统计的回归模型或者说计量经济学的模型角度来讨论的。第九章以后主要是从数据挖掘、人工智能的角度来讨论。
回归模型偏向对数值型变量的估值,而挖掘模型更偏向判别离散结果,如这个图片中的数字是0-9中的哪一个。
正文
一,建立回归模型的方法论
| 步骤 | 名称 | 说明 |
|---|---|---|
| 1 | 理论或假说的陈述 | 凯恩斯设想:边际消费倾向 |
| 2 | 数学模型的设定 | 准确的确定性的模型: Y = β 1 + β 2 X , ∥ β 2 ∥ < 1 Y=β_1+β_2X,\|β_2\|<1 Y=β1+β2X,∥β2∥<1 |
| 3 | 回归模型(或计量经济学模型)的设定 | 非确定性模型-随机变量(误差项): Y = β 1 + β 2 X + μ Y=β_1+β_2X+μ Y=β1+β2X+μ 模型设置错误会产生选择性偏误 |
| 4 | 获得数据 | 自然科学来自于实验、社会科学来自于非实验 |
| 5 | 模型的估计 | 运用统计回归分析方法 |
| 6 | 模型的检验 | 统计学检验:拟合优度、显著性 计量经济学检验:误差项的正态性 、序列相关,异方差,多重共线性等 预测检验:主要是检验参数估计量的稳定性以及对样本容量变化时的灵敏度,即所谓超样本特性。 |
| 7 | 预测或预报 | 结构分析,经济预测,政策评价,检验与发展经济理论 |
| 8 | 利用模型做出决策 | 根据结果给定建议或方案 |
备注1:预测检验的具体检验方法为:
-
利用扩大了的样本重新估计模型参数的新估计值,与原来估计值比较,并检验二者差异的显著性;
-
将模型用于样本以外预测,将预测值与实际观测值进行比较,并检验二者差异的显著性
备注2:结构分析的方法:
-
弹性分析,某一变量的相对变化引起的另一变量的相对变化,即变量的变化率之比,比率关系
-
乘数分析,某一变量的绝对变化引起的另一变量的绝对变化,即变量的变化之比,倍数关系
-
比较静力分析,经济系统不同平衡位置之间的联系
二,一元线性回归模型
1,总体回归函数
(1) 总体回归函数 (又叫条件期望函数)
E ( E( E(Y| X i ) = f ( X i ) X_i)=f(X_i) Xi)=f(Xi)
表示,给定 X i X_i Xi的条件下,总体Y的均值与 X i X_i Xi存在着某种函数关系f()。
该函数关系f()的形式是一个重要问题,一般依照某种理论假设或实际经验等给出。
备注:回归、回归方程、回归函数、回归模型不加以区分,均代表相同意思。
(2) 当f()为一元线性假设时,总体回归函数如下:
E ( E( E(Y| X i ) = β 0 + β 1 X X_i)=β_0+β_1X Xi)=β0+β1X
β 0 、 β 1 β_0、β_1 β0、β1分别是线性函数的截距、斜率,统称回归系数。
(3) 对于线性的解释
| 线性举例 | 非线性举例 | |
|---|---|---|
| 对变量为线性 | Y = β 0 + β 1 X Y=β_0+β_1X Y=β0+β1X | Y = β 0 + β 1 X 2 Y=β_0+β_1X^2 Y=β0+β1X2 |
| 对参数为线性 | Y = β 0 + β 1 X Y=β_0+β_1X Y=β0+β1X | Y = β 0 + β 1 2 X Y=β_0+β_1^2X Y=β0+β12X |
两种解释中,我们定义所讨论的“线性回归模型”中的“线性”是指的针对于参数为线性,即回归系数为一次方出现的模型,因此对于解释变量X为非线性、可多次方出现的情况,即后续要讨论的广义线性模型。
(4) 误差项
我们可以得到,样本值与总体回归函数的差值
u i = Y i − E ( u_i = Y_i -E( ui=Yi−E(Y| X i ) = Y i − ( β 0 + β 1 X ) X_i)=Y_i -(β_0+β_1X) Xi)=Yi−(β0+β1X)
则
Y i = E ( Y_i = E( Yi=E(Y| X i ) + u i = β 0 + β 1 X + u i X_i) + u_i =β_0+β_1X+u_i Xi)+ui=β0+β1X+ui
如何理解上述方程?
将其理解为两个组成部分
- E ( E( E(Y| X i ) X_i) Xi)表示给定X后Y的平均值,代表系统性的或确定性的部分
- u i u_i ui表示所有可能会影响到Y但是有没有包括进回归模型中的那些变量的代替或代理变量,代表随机或非系统性的部分
- 如果这些没有包括进模型的变量,与X不相关,且对于模型起不到决定性作用,那么上述方程没有什么问题;如果相反,则会出现omitted variables bias的情况
把等式两边取条件期望
Y i = E ( Y_i = E( Yi=E(Y| X i ) + u i X_i) + u_i Xi)+ui
E ( Y i ∣ X i ) = E ( E ( E(Y_i|X_i) = E(E( E(Yi∣Xi)=E(E(Y| X i ) ) + E ( u i ∣ X i ) X_i)) + E(u_i|X_i) Xi))+E(ui∣Xi)
E ( Y i ∣ X i ) = E ( E(Y_i|X_i) = E( E(Yi∣Xi)=E(Y| X i ) + E ( u i ∣ X i ) X_i) + E(u_i|X_i) Xi)+E(ui∣Xi)
令
E ( Y i ∣ X i ) = E ( E(Y_i|X_i) = E( E(Yi∣Xi)=E(Y| X i ) X_i) Xi)
则
E ( u i ∣ X i ) = 0 E(u_i|X_i)=0 E(ui∣Xi)=0
如果想让回归函数对应的回归曲线穿过Y的条件期望,则随机扰动项,即误差项的条件均值为零。
2,样本回归函数
通过样本数据,样本回归模型的结果如下:
Y ^ = β 0 ^ + β 1 ^ X i \hat{Y}=\hat{β_0}+\hat{β_1}X_i Y^=β0^+β1^Xi
加入随机形式的表达如下:
Y = β 0 ^ + β 1 ^ X i + u i ^ Y=\hat{β_0}+\hat{β_1}X_i+\hat{u_i} Y=β0^+β1^Xi+ui^
所以,我们能够得到
β 0 ^ \hat{β_0} β0^是 β 0 β_0 β0的估计量
β 1 ^ \hat{β_1} β1^是 β 1 β_1 β1的估计量
μ i ^ \hat{μ_i} μi^是 μ i μ_i μi的估计量,表示样本与总体的差异
每次总体抽样的结果不一样,得到的样本回归函数也不同,那如何能够让样本回归函数尽可能的趋近于总体回归函数呢?接下来我们研究模型的参数估计。
三,一元线性模型的估计量
最经典的线性回归模型的估计方法是普通最小二乘(Ordinary Least Squares, OLS)估计方法,除此之外还有极大似然(Maximum Likelihood)估计方法,对于一般线性回归模型,二者得到的结果是相同的。
备注:以上方法的估计量实际是点估计,与点估计对应的,还有区间估计,但是区间估计需要有概率分布的信息。
1,OLS
根据之前的说明,我们知道,当用样本来估计总体时,将产生误差项
由
Y i = Y i ^ + μ i ^ = β 0 ^ + β 1 ^ X i + μ i ^ Y_i = \hat{Y_i} +\hat{μ_i} =\hat{β_0}+\hat{β_1}X_i+\hat{μ_i} Yi=Yi^+μi^=β0^+β1^Xi+μi^
得
μ i ^ = Y i − Y i ^ = Y i − β 0 ^ − β 1 ^ X i \hat{μ_i} = Y_i - \hat{Y_i} =Y_i-\hat{β_0}-\hat{β_1}X_i μi^=Yi−Yi^=Yi−β0^−β1^Xi
OLS的思想即是求得回归参数的估计量,使得 ∑ μ ^ i 2 \sum{\hat{μ}^2_i} ∑μ^i2最小,即
目标函数最小
O = ∑ μ ^ i 2 = ∑ ( Y i − β 0 ^ − β 1 ^ X i ) 2 \sum{\hat{μ}^2_i}=\sum(Y_i-\hat{β_0}-\hat{β_1}X_i)^2 ∑μ^i2=∑(Yi−β0^−β1^Xi)2
求目标函数极小值的过程:
- ∂ O ∂ β 0 \frac{\partial O}{\partialβ_0} ∂β0∂O= 2 ∑ ( Y i − β 0 ^ − β 1 ^ X i ) ∗ ( − 1 ) = ∑ μ i ^ = 0 2\sum(Y_i-\hat{β_0}-\hat{β_1}X_i)*(-1)=\sum \hat{μ_i}=0 2∑(Yi−β0^−β1^Xi)∗(−1)=∑μi^=0
- ∂ O ∂ β 1 \frac{\partial O}{\partialβ_1} ∂β1∂O= 2 ∑ ( Y i − β 0 ^ − β 1 ^ X i ) ∗ ( − X i ) = ∑ μ i ^ X i = 0 2\sum(Y_i-\hat{β_0}-\hat{β_1}X_i)*(- X_i)=\sum \hat{μ_i}X_i=0 2∑(Yi−β0^−β1^Xi)∗(−Xi)=∑μi^Xi=0
即
∑ Y i − n β 0 ^ − β 1 ^ ∑ X i = 0 \sum Y_i-n\hat{β_0}- \hat{β_1}\sum X_i=0 ∑Yi−nβ0^−β1^∑Xi=0……………………………………等式1
∑ X i Y i − β 0 ^ ∑ X i − β 1 ^ ∑ X i 2 = 0 \sum X_iY_i-\hat{β_0}\sum X_i-\hat{β_1}\sum X_i^2=0 ∑XiYi−β0^∑Xi−β1^∑Xi2=0……………………………等式2
等式1,同时除n变换
则
∑ Y i / n − β 0 ^ − β 1 ^ ∑ X i / n = 0 \sum Y_i/n-\hat{β_0}- \hat{β_1}\sum X_i/n=0 ∑Yi/n−β0^−β1^∑Xi/n=0
y ‾ − β 0 ^ − β 1 ^ x ‾ = 0 \overline{y}-\hat{β_0}-\hat{β_1}\overline{x}=0 y−β0^−β1^x=0
(其中, y ‾ = ∑ Y i / n , x ‾ = ∑ X i / n \overline{y}=\sum Y_i/n,\overline{x}=\sum X_i/n y=∑Yi/n,x=∑Xi/n)
得
- β 0 ^ = y ‾ − β 1 ^ x ‾ = 0 \hat{β_0} =\overline{y}-\hat{β_1}\overline{x}=0 β0^=y−β1^x=0
将 β 0 ^ \hat{β_0} β0^代入到等式2,
得
∑ X i Y i − ( y ‾ − β 1 ^ x ‾ ) ∑ X i − β 1 ^ ∑ X i 2 = 0 \sum X_iY_i-(\overline{y}-\hat{β_1}\overline{x})\sum X_i-\hat{β_1}\sum X_i^2=0 ∑XiYi−(y−β1^x)∑Xi−β1^∑Xi2=0
∑ X i Y i − y ‾ ∑ X i + β 1 ^ x ‾ ∑ X i − β 1 ^ ∑ X i 2 = 0 \sum X_iY_i-\overline{y}\sum X_i+\hat{β_1}\overline{x}\sum X_i-\hat{β_1}\sum X_i^2=0 ∑XiYi−y∑Xi+β1^x∑Xi−β1^∑Xi2=0
∑ X i Y i − y ‾ ∑ X i = β 1 ^ ( ∑ X i 2 − x ‾ ∑ X i ) \sum X_iY_i-\overline{y}\sum X_i=\hat{β_1}(\sum X_i^2-\overline{x}\sum X_i) ∑XiYi−y∑Xi=β1^(∑Xi2−x∑Xi)
β 1 ^ = ∑ X i Y i − y ‾ ∑ X i ∑ X i 2 − x ‾ ∑ X i = ∑ ( X i Y i − y ‾ X i ) ∑ ( X i 2 − x ‾ X i ) = ∑ ( X i Y i − y ‾ X i − x ‾ Y i + x ‾ Y i ) ∑ ( X i 2 − 2 x ‾ X i + x ‾ X i ) \hat{β_1}=\frac{\sum X_iY_i-\overline{y}\sum X_i}{\sum X_i^2-\overline{x}\sum X_i}=\frac{\sum (X_iY_i-\overline yX_i)}{\sum (X_i^2-\overline xX_i)}=\frac{\sum (X_iY_i-\overline yX_i-\overline xY_i+\overline xY_i)}{\sum (X_i^2-2\overline xX_i+\overline xX_i)} β1^=∑Xi2−x∑Xi∑XiYi−y∑Xi=∑(Xi2−xXi)∑(XiYi−yXi)=∑(Xi2−2xXi+xXi)∑(XiYi−yXi−xYi+xYi)
因为
∑ x ‾ Y i = x ‾ ∑ Y i = n x y ‾ = ∑ x y ‾ \sum\overline xY_i=\overline x\sum Y_i=n\overline{xy}=\sum \overline{xy} ∑xYi=x∑Yi=nxy=∑xy
同理
∑ x ‾ X i = x ‾ ∑ X i = n x ‾ 2 = ∑ x ‾ 2 \sum\overline xX_i=\overline x\sum X_i=n\overline{x}^2=\sum \overline{x}^2 ∑xXi=x∑Xi=nx2=∑x2
所以
- β 1 ^ = ∑ ( X i Y i − y ‾ X i − x ‾ Y i + x ‾ Y i ) ∑ ( X i 2 − 2 x ‾ X i + x ‾ X i ) = ∑ ( X i Y i − y ‾ X i − x ‾ Y i + x y ‾ ) ∑ ( X i 2 − 2 x ‾ X i + x ‾ 2 ) = ∑ ( X i − x ‾ ) ( Y i − y ‾ ) ∑ ( X i − x ‾ ) 2 \hat{β_1}=\frac{\sum (X_iY_i-\overline yX_i-\overline xY_i+\overline xY_i)}{\sum (X_i^2-2\overline xX_i+\overline xX_i)}=\frac{\sum (X_iY_i-\overline yX_i-\overline xY_i+\overline {xy})}{\sum (X_i^2-2\overline xX_i+\overline x^2)}=\frac{\sum (X_i-\overline x)(Y_i-\overline y)}{\sum(X_i-\overline x)^2} β1^=∑(Xi2−2xXi+xXi)∑(XiYi−yXi−xYi+xYi)=∑(Xi2−2xXi+x2)∑(XiYi−yXi−xYi+xy)=∑(Xi−x)2∑(Xi−x)(Yi−y)
另外根据等式2,得
∑ μ i ^ X i = ( Y i − β 0 − β 1 X 1 ) X i = 0 \sum\hat{μ_i}X_i=(Y_i -β_0-β_1X_1)X_i=0 ∑μi^Xi=(Yi−β0−β1X1)Xi=0……………………………等式3
c o v ( X i , μ i ^ ) = E ( X i − E ( x ) ) ( μ i ^ − E ( μ ) ) = E ( X i μ ^ i ) − E ( X i ) E ( μ ^ i ) cov(X_i,\hat{μ_i})=E(X_i-E(x))(\hat{μ_i}-E(μ))=E(X_i\hat μ_i)-E(X_i)E(\hat μ_i) cov(Xi,μi^)=E(Xi−E(x))(μi^−E(μ))=E(Xiμ^i)−E(Xi)E(μ^i)
因为 E ( μ ^ i ) = 0 E(\hat μ_i)=0 E(μ^i)=0,所以
c o v ( X i , μ i ^ ) = E ( X i μ ^ i ) = ∑ μ i ^ X i n = 0 cov(X_i,\hat{μ_i})=E(X_i\hat μ_i)=\frac{\sum\hat{μ_i}X_i}{n}=0 cov(Xi,μi^)=E(Xiμ^i)=n∑μi^Xi=0
即,残差 μ ^ \hat{μ} μ^与 X i X_i Xi不相关
2,最小二乘回归的基本假定
| 假设 | 假设说明 | 解释 | |
|---|---|---|---|
| 解释变量假设 | 确定性假设 | X是固定值、非随机变量 | 保证模型可建的基本假设-因为模型是条件期望即条件回归 |
| 非完全共线性假设 | 共线性导致解释变量冗余 | 完全共线性导致求解不唯一,部分共线性导致求解不稳定 | |
| 与残差不相关 | c o v ( X i , μ i ) = 0 或 E ( X i ∗ μ i ) = 0 cov(X_i,μ_i)=0 或 E(X_i*μ_i)=0 cov(Xi,μi)=0或E(Xi∗μi)=0 | 由OLS估计,残差平方和对参数 β 1 β_1 β1求偏导数为零求得 |
| 假设 | 假设说明 | 解释 | |
|---|---|---|---|
| 随机残差项假设 | 零均值假设 | E( μ i μ_i μi| X i X_i Xi)=0 | 带有截距项的OLS估计中可推导出 |
| 同方差假设 | var( μ i μ_i μi| X i X_i Xi)= σ 2 σ^2 σ2 | 如果残差同方差成立,则var( y i y_i yi| X i X_i Xi)= σ 2 σ^2 σ2也成立 | |
| 序列不相关 | var( μ i , μ j μ_i, μ_j μi,μj| X i , X j X_i, X_j Xi,Xj)=0, i≠j | ||
| 正态性假设 | μ i μ_i μi~ N ( 0 , σ 2 ) N(0,σ^2) N(0,σ2) | 参数估计时不需要正态性假设,估计量推断时需要 |
3,估计量的均值与方差
我们已知
β 1 ^ = ∑ ( X i − x ‾ ) ( Y i − y ‾ ) ∑ ( X i − x ‾ ) 2 \hat{β_1}=\frac{\sum (X_i-\overline x)(Y_i-\overline y)}{\sum(X_i-\overline x)^2} β1^=∑(Xi−x)2∑(Xi−x)(Yi−y), β 0 ^ = y ‾ − β 1 ^ x ‾ = 0 \hat{β_0} =\overline{y}-\hat{β_1}\overline{x}=0 β0^=y−β1^x=0
如果对总体数据进行中心化处理,即 x i = X i − x ‾ , y i = Y i − y ‾ x_i = X_i-\overline x, y_i = Y_i-\overline y xi=Xi−x,yi=Yi−y,则
β 1 ^ = ∑ x i y i ∑ x i 2 \hat{β_1}=\frac{\sum x_iy_i}{\sum x_i^2} β1^=∑xi2∑xiyi
由于X是固定变量, 令 k i = x i ∑ x i 2 令k_i=\frac{x_i}{\sum x_i^2} 令ki=∑xi2xi,则
- β 1 ^ = ∑ k i y i \hat{β_1}=\sum k_iy_i β1^=∑kiyi(………………线性的)
β 1 ^ = ∑ k i ( β 0 + β 1 x i + μ i ) = ∑ ( β 0 k i + β 1 k i x i + k i μ i ) \hat{β_1}=\sum k_i(β_0+β_1x_i+μ_i)=\sum (β_0k_i+β_1k_ix_i+k_iμ_i) β1^=∑ki(β0+β1xi+μi)=∑(β0ki+β1kixi+kiμi)
又因为数据做了中心化处理,所以 ∑ x i = 0 , 所 以 ∑ k i = 0 \sum x_i=0,所以\sum k_i=0 ∑xi=0,所以∑ki=0,则
β 1 ^ = β 0 ∑ k i + ∑ β 1 k i x i + ∑ k i μ i = β 1 ∑ k i x i + ∑ k i μ i \hat{β_1}=β_0\sum k_i+\sum β_1k_ix_i+ \sum k_iμ_i=β_1\sum k_ix_i+ \sum k_iμ_i β1^=β0∑ki+∑β1kixi+∑kiμi=β1∑kixi+∑kiμi
β 1 ^ = β 1 + ∑ k i μ i \hat{β_1}=β_1+\sum k_iμ_i β1^=β1+∑kiμi
E ( β 1 ^ ) = E ( β 1 + ∑ k i μ i ) = E ( β 1 ) + E ( ∑ k i μ i ) = E ( β 1 ) + ∑ k i E ( μ i ) E(\hat{β_1})=E(β_1+\sum k_iμ_i)=E(β_1)+E(\sum k_iμ_i)=E(β_1)+\sum k_iE(μ_i) E(β1^)=E(β1+∑kiμi)=E(β1)+E(∑kiμi)=E(β1)+∑kiE(μi)
- E ( β 1 ^ ) = E ( β 1 ) = β 1 E(\hat{β_1})=E(β_1)=β_1 E(β1^)=E(β1)=β1(………………无偏性的)
v a r ( β 1 ^ ) = E ( β 1 ^ − E ( β 1 ^ ) ) 2 = E ( β 1 ^ − β 1 ) ) 2 = E ( ∑ k i μ i ) 2 var(\hat{β_1})=E(\hat{β_1}-E(\hat{β_1}))^2=E(\hat{β_1}-β_1))^2=E(\sum k_iμ_i)^2 var(β1^)=E(β1^−E(β1^))2=E(β1^−β1))2=E(∑kiμi)2
因为假设残差不自相关 E ( μ i , μ j ) = 0 E(μ_i,μ_j)=0 E(μi,μj)=0,所以展开平方公式,得
v a r ( β 1 ^ ) = E ( k 1 2 μ 1 2 + k 2 2 μ 2 2 + . . . + k n 2 μ n 2 ) = σ 2 ∑ k i 2 var(\hat{β_1})=E(k_1^2μ_1^2+k_2^2μ_2^2+...+k_n^2μ_n^2)=σ^2\sum k_i^2 var(β1^)=E(k12μ12+k22μ22+...+kn2μn2)=σ2∑ki2
- v a r ( β 1 ^ ) = σ 2 ∑ x i 2 var(\hat{β_1})=\frac{σ^2}{\sum x_i^2} var(β1^)=∑xi2σ2
4,高斯-马尔可夫定理
在上述给定的经典线性回归模型的假定下,OLS的估计量是BLUE的,即最佳线性无偏估计量(best linear unbiased estimatior,BLUE):
- 线性的:参数线性
- 无偏性:期望值等于真实值
- 有效性:最小方差的无偏估计量
5,最大似然估计
除上述假设外,若残差项再服从独立且正态分布 N I D ( 0 , σ 2 ) NID(0,σ^2) NID(0,σ2)假设,则我们可以通过ML进行估计。
ML估计的残差方差是有偏的,但是在大样本的情况下,趋于一致性。
所以ML又叫大样本方法,并且ML除了线性模型,也可以对非线性模型进行估值。
Y = Y ^ + μ = E ( Y ∣ X ) + μ = β ^ 0 + β ^ 1 X + μ Y =\hat Y + μ=E(Y|X)+μ=\hat β_0+\hat β_1X+μ Y=Y^+μ=E(Y∣X)+μ=β^0+β^1X+μ
若 μ μ μ~ N I D ( 0 , σ μ 2 ) NID(0,σ_μ^2) NID(0,σμ2),
有 μ μ μ的线性组合服从的分布不变,
且又有残差有零均值假设E(μ|X)=0,则
E ( Y ∣ X ) = E ( Y ∣ X ) + E ( μ ∣ X ) = E ( Y ∣ X ) = β ^ 0 + β ^ 1 X E(Y|X)=E(Y|X)+E(μ|X)=E(Y|X)=\hat β_0+\hat β_1X E(Y∣X)=E(Y∣X)+E(μ∣X)=E(Y∣X)=β^0+β^1X
因为 Y ^ \hat Y Y^是回归得到的固定值,非随机变量
v a r ( Y ) = v a r ( Y ^ + μ ) = v a r ( μ ) = σ μ 2 var(Y)=var(\hat Y + μ)=var(μ)=σ_μ^2 var(Y)=var(Y^+μ)=var(μ)=σμ2
所以, Y Y Y~ N I D ( β ^ 0 + β ^ 1 X , σ μ 2 ) NID(\hat β_0+\hat β_1X, σ_μ^2) NID(β^0+β^1X,σμ2)
得到 y i y_i yi的概率密度
P ( y i ) = 1 σ 2 π e x p ( − 1 2 σ 2 ( y i − β ^ 0 − β ^ 1 x i ) 2 ) P(y_i)=\frac{1}{σ\sqrt 2π}exp(-\frac{1}{2σ^2}(y_i - \hat β_0-\hat β_1x_i)^2) P(yi)=σ2π1exp(−2σ21(yi−β^0−β^1xi)2)
定义目标函数L
L ( β ^ 0 , β ^ , σ 2 ) = P ( y 1 ) ⋅ P ( y 2 ) . . . ⋅ P ( y n ) = 1 ( σ 2 π ) n e x p ( − 1 2 σ 2 ∑ i = 1 i = n ( y i − β ^ 0 − β ^ 1 x i ) 2 ) L(\hat β_0,\hat β,σ^2)=P(y_1)·P(y_2)...·P(y_n)=\frac{1}{(σ\sqrt 2π)^n}exp(-\frac{1}{2σ^2}\sum_{i=1}^{i=n}(y_i - \hat β_0-\hat β_1x_i)^2) L(β^0,β^,σ2)=P(y1)⋅P(y2)...⋅P(yn)=(σ2π)n1exp(−2σ21∑i=1i=n(yi−β^0−β^1xi)2)
L ∗ = l n ( L ) = − n l n ( σ 2 π ) − 1 2 σ 2 ∑ i = 1 i = n ( y i − β ^ 0 − β ^ 1 x i ) 2 L^*=ln(L)=-nln(σ\sqrt 2π)-\frac{1}{2σ^2}\sum_{i=1}^{i=n}(y_i - \hat β_0-\hat β_1x_i)^2 L∗=ln(L)=−nln(σ2π)−2σ21∑i=1i=n(yi−β^0−β^1xi)2
对 L ∗ L^* L∗求极大值,即是等价于对 ∑ i = 1 i = n ( y i − β ^ 0 − β ^ 1 x i ) 2 \sum_{i=1}^{i=n}(y_i - \hat β_0-\hat β_1x_i)^2 ∑i=1i=n(yi−β^0−β^1xi)2求极小值,等价于OLS的目标函数
因为目标函数一致,所以求得的参数一致。
备注:极大似然法估计出的回归参数与OLS一致,但是对于残差项的方差则是有偏的,随着样本量的增加是渐进无偏的。
四,一元线性回归模型的评价-统计学检验
1,拟合优度 R 2 R^2 R2
由回归方程
Y i = β 0 ^ + β 1 ^ X i + μ ^ i Y_i=\hat{β_0} + \hat{β_1}X_i+\hat μ_i Yi=β0^+β1^Xi+μ^i
代入均值,我们可得
Y ‾ i = β 0 ^ + β 1 ^ X ‾ i \overline Y_i=\hat{β_0} + \hat{β_1}\overline X_i Yi=β0^+β1^Xi
两式相减,得
Y i − Y ‾ i = β 1 ^ ( X i − X ‾ ) + μ ^ i Y_i-\overline Y_i=\hat{β_1}(X_i-\overline X)+\hat μ_i Yi−Yi=β1^(Xi−X)+μ^i
总平方和为
∑ ( Y i − Y ‾ i ) 2 = ∑ [ β 1 ^ ( X i − X ‾ ) + μ ^ i ] 2 = ∑ β 1 ^ 2 ( X i − X ‾ ) 2 + ∑ μ ^ i 2 + 2 β 1 ^ ∑ μ ^ i ( X i − X ‾ ) \sum (Y_i-\overline Y_i)^2=\sum[\hat{β_1}(X_i-\overline X)+\hat μ_i]^2=\sum\hat{β_1}^2(X_i-\overline X)^2+\sum \hat μ_i^2+2\hat{β_1}\sum \hat μ_i(X_i-\overline X) ∑(Yi−Yi)2=∑[β1^(Xi−X)+μ^i]2=∑β1^2(Xi−X)2+∑μ^i2+2β1^∑μ^i(Xi−X)
由于等式3,知
∑ μ ^ i X i = 0 \sum\hat μ_iX_i=0 ∑μ^iXi=0, ∑ μ ^ i = 0 \sum\hat μ_i=0 ∑μ^i=0
所以, 2 β 1 ^ ∑ μ ^ i ( X i − X ‾ ) = ∑ μ ^ i ⋅ 2 β 1 ^ ( X i − X ‾ ) = 0 2\hat{β_1}\sum \hat μ_i(X_i-\overline X)=\sum \hat μ_i·2\hat{β_1}(X_i-\overline X)=0 2β1^∑μ^i(Xi−X)=∑μ^i⋅2β1^(Xi−X)=0
总平方和为
∑ ( Y i − Y ‾ i ) 2 = ∑ β 1 ^ 2 ( X i − X ‾ ) 2 + ∑ μ ^ i 2 = ∑ ( Y ^ i − Y ‾ ) 2 + ∑ μ ^ i 2 \sum (Y_i-\overline Y_i)^2=\sum\hat{β_1}^2(X_i-\overline X)^2+\sum \hat μ_i^2= \sum (\hat Y_i-\overline Y)^2+\sum \hat μ_i^2 ∑(Yi−Yi)2=∑β1^2(Xi−X)2+∑μ^i2=∑(Y^i−Y)2+∑μ^i2
即
总平方和(TSS) = 回归平方和(ESS) + 残差平方和(RSS)
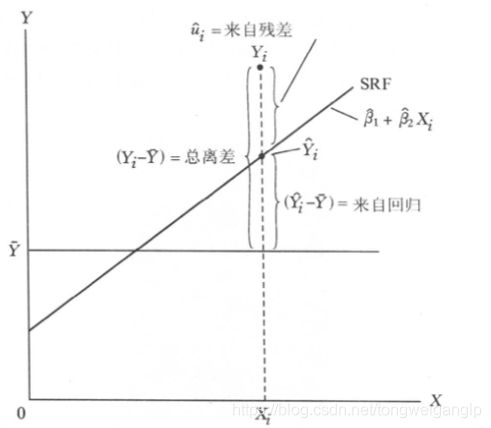
我们定义拟合优度(又叫判定系数)为:
R 2 = E S S T S S = 1 − R S S T S S = 1 − ∑ μ 2 ∑ ( Y i − Y ‾ i ) 2 R^2 =\frac{ESS}{TSS}=1-\frac{RSS}{TSS}=1-\frac{\sum μ^2}{\sum (Y_i-\overline Y_i)^2} R2=TSSESS=1−TSSRSS=1−∑(Yi−Yi)2∑μ2
因为 β 1 = ∑ ( X i − x ‾ ) ( Y i − y ‾ ) ∑ ( X i − x ‾ ) 2 β_1=\frac{\sum (X_i-\overline x)(Y_i-\overline y)}{\sum(X_i-\overline x)^2} β1=∑(Xi−x)2∑(Xi−x)(Yi−y),代入得
R 2 = E S S T S S = ∑ β 1 ^ 2 ( X i − X ‾ ) 2 ∑ ( Y i − Y ‾ i ) 2 = ∑ ( X i − x ‾ ) 2 ( Y i − y ‾ ) 2 ∑ ( X i − X ‾ ) 2 ∑ ( Y i − Y ‾ i ) 2 = [ c o v ( X i , Y i ) ] 2 σ x 2 σ y 2 R^2 =\frac{ESS}{TSS}=\frac{\sum\hat{β_1}^2(X_i-\overline X)^2}{\sum (Y_i-\overline Y_i)^2}=\frac{\sum (X_i-\overline x)^2(Y_i-\overline y)^2}{\sum(X_i-\overline X)^2\sum (Y_i-\overline Y_i)^2}=\frac{[cov(X_i,Y_i)]^2}{σ_x^2σ_y^2} R2=TSSESS=∑(Yi−Yi)2∑β1^2(Xi−X)2=∑(Xi−X)2∑(Yi−Yi)2∑(Xi−x)2(Yi−y)2=σx2σy2[cov(Xi,Yi)]2
所以, R 2 = p e r s o n 相 关 系 数 的 平 方 R^2=person相关系数的平方 R2=person相关系数的平方
注意1:对于截距项是零的回归模型,OLS目标函数只能得到一个偏导数方程,无法推论出 ∑ μ ^ i = 0 \sum \hat μ_i=0 ∑μ^i=0,则
∑ ( Y i − Y ‾ i ) 2 = ∑ ( Y ^ i − Y ‾ ) 2 + ∑ μ ^ i 2 + ∑ μ ^ i ⋅ 2 β 1 ^ ( X i − X ‾ ) \sum (Y_i-\overline Y_i)^2= \sum (\hat Y_i-\overline Y)^2+\sum \hat μ_i^2+\sum \hat μ_i·2\hat{β_1}(X_i-\overline X) ∑(Yi−Yi)2=∑(Y^i−Y)2+∑μ^i2+∑μ^i⋅2β1^(Xi−X)
即过原点的回归模型来说,拟合优度 R 2 R^2 R2并不保证非负数。
注意2:要避免进入 R 2 R^2 R2陷阱,即过度追求高 R 2 R^2 R2的值,低值并非意味着模型没有价值。
2,残差项的正态性假设
我们假定残差项:正态且独立分布,即μ~ N I D ( 0 , σ 2 ) NID(0,σ^2) NID(0,σ2)
理由如下:
- 根据中心极限定理,大部分情况都会符合正态分布
- 如果假设成立, β 0 、 β 1 β_0、β_1 β0、β1是残差μ的线性组合,也将符合正态分布,简化了假设检验的工作
- 理论分布比较简单
对于不符合正态分布的情况,我们会有相应的处理方式。
3,方程的显著性检验-F检验(方差分析)
对于方程来说,如果变量的参数都是零,则说明方程是无效的。
为了验证方程的显著性,我们通过对总体平方和的分解,来构造方差分析中的F统计量。
由
∑ ( Y i − Y ‾ i ) 2 = ∑ β 1 ^ 2 ( X i − X ‾ ) 2 + ∑ μ ^ i 2 = ∑ ( Y ^ i − Y ‾ ) 2 + ∑ μ ^ i 2 \sum (Y_i-\overline Y_i)^2=\sum\hat{β_1}^2(X_i-\overline X)^2+\sum \hat μ_i^2= \sum (\hat Y_i-\overline Y)^2+\sum \hat μ_i^2 ∑(Yi−Yi)2=∑β1^2(Xi−X)2+∑μ^i2=∑(Y^i−Y)2+∑μ^i2
知
总平方和(TSS) = 回归平方和(ESS) + 残差平方和(RSS)
| 平方和 | 自由度 | 均方 | F统计量 | |
|---|---|---|---|---|
| 回归平方和 | ESS | k | E S S k \frac {ESS}{k} kESS | F = E S S / k R S S / ( n − k − 1 ) F=\frac{ESS/k}{RSS/(n-k-1)} F=RSS/(n−k−1)ESS/k~F(k,n-k-1) |
| 残差平方和 | RSS | n-k-1 | R S S n − k − 1 \frac {RSS}{n-k-1} n−k−1RSS | |
| 总平方和 | TSS | n-1 |
原假设 H 0 : β 1 = . . . = β k = 0 ( 注 意 : 截 距 项 β 0 不 再 此 假 设 中 , 因 为 E S S 的 表 达 式 中 没 有 β 0 ) H_0: β_1 = ...=β_k=0 (注意:截距项β_0不再此假设中,因为ESS的表达式中没有β_0) H0:β1=...=βk=0(注意:截距项β0不再此假设中,因为ESS的表达式中没有β0)
备择假设 H 1 : 不 全 为 0 H_1: 不全为 0 H1:不全为0
由于F统计量可以写成拟合优度的表达式: F = ( 1 − R 2 ) / k R 2 / ( n − k − 1 ) F=\frac {(1-R^2)/k}{R^2/(n-k-1)} F=R2/(n−k−1)(1−R2)/k
所以,F检验实际上也是对拟合优度 R 2 R^2 R2的显著性检验
注意:本章假设回归模型为 Y = β 0 + β 1 X 1 + . . . β k X k + μ Y=β_0+β_1X_1+...β_kX_k+μ Y=β0+β1X1+...βkXk+μ,即产生 Y , X 1 , . . . , X k Y,X_1,...,X_k Y,X1,...,Xk,共 k+1 个变量,此时方程的自由度是k=(k+1)-1
同理上述方差分析表中,ESS的方程中也是k+1个变量,自由度为是k=(k+1)-1,RSS为n-(k+1)=n-k-1。
如果参数的设置是由 β 1 β_1 β1开始的, Y = β 1 + β 2 X 1 + . . . β k X k + μ Y=β_1+β_2X_1+...β_kX_k+μ Y=β1+β2X1+...βkXk+μ则ESS自由度变为k-1,RSS的自由度变为n-k。
4,变量的显著性检验-t检验
对每个变量进行显著性判断,通过构造t统计量进行推断
t = β i ^ − β i S β ^ i t = \frac {\hat{β_i}-β_i}{S_{\hat β_i}} t=Sβ^iβi^−βi
原假设 H 0 : β i = 0 H_0:β_i = 0 H0:βi=0
备择假设 H 1 : β i ≠ 0 H_1:β_i ≠ 0 H1:βi̸=0
五,多元线性回归模型
对于多元线性回归模型来说,假设、求解、显著性检验的推断过程和逻辑是一致的。
值得注意的是,对于多元回归模型,拟合优度需要修正:
随着解释变量的增加,拟合优度会至少不会变差,那么真的是越多的变量越好吗?
The Answer Is No
调整后的拟合优度:
R ‾ 2 = 1 − ( 1 − R 2 ) n − 1 n − k \overline{R}^2=1- (1-R^2)\frac{n-1}{n-k} R2=1−(1−R2)n−kn−1
k为包括截距项的估计参数的个数
参考:
1,计量经济学基础,古扎拉蒂