非对称算法基于RSA算法
1、非对称加密过程:
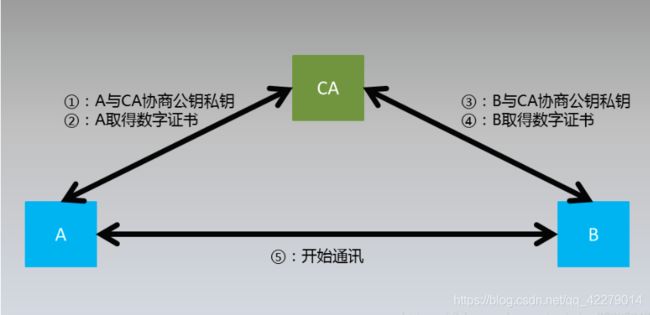
假如现实世界中存在A和B进行通讯,为了实现在非安全的通讯通道上实现信息的保密性、完整性、可用性(即信息安全的三个性质),A和B约定使用非对称加密通道进行通讯,具体过程如下:
说明:
国内目前使用双证书体系,即用户同时拥有签名证书、加密证书两张证书。签名证书是用户的身份认证,是和CA协商的结果,可用于对用户A的身份验证;加密证书是用来对信息进行加密,是用户和秘钥管理系统生成。我们在这里假设都适合CA进行交互。
①:此过程是生成公钥私钥的过程,我们这里基于RSA算法实现,RSA算法的详细说明在后面讲解。
②:此过程是CA对用户的身份进行签名,目的验证A的身份。这样在A与B通讯的过程中,A可以把自己的数字签名发给B,B得到此数字签名后就可以通过CA的公钥对其进行解密并进行身份验证,具体过程在后面讲解。
③④同理。
⑤:A对要传输的信息进行加密并传输,B接受到以后进行解密的过程。
2、RSA算法:
RSA原理:RSA算法基于一个十分简单的数论事实:将两个大素数相乘十分容易,但是想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥。
算法:
(1)选择两个不同的大素数p和q;
(2)计算乘积n=pq和Φ(n)=(p-1)(q-1);
(3)选择大于1小于Φ(n)的随机整数e,使得gcd(e,Φ(n))=1;注:gcd即最大公约数。
(4)计算d使得d*e=1mod Φ(n);注:即d*e mod Φ(n) =1。
(5)对每一个密钥k=(n,p,q,d,e),定义加密变换为Ek(x)=xe mod n,解密变换为Dk(x)=yd mod n,这里x,y∈Zn;
(6)p,q销毁,以{e,n}为公开密钥,{d,n}为私有密钥。
实例:
1. 假设p = 3、q = 11(p,q都是素数即可。),则N = pq = 33;
2. r =Φ(n)= (p-1)(q-1) = (3-1)(11-1) = 20;
3. 根据gcd(e,Φ(n))=1,即gcd(e,20)=1,令e=3,则,d = 7。(两个数交换一下也可以。)
到这里,公钥和密钥已经确定。公钥为(N, e) = (33, 3),密钥为(N, d) = (33, 7)。
附上代码
package com.su.demo.utils;
/**
* @author Su
* @version 1.0
* @date 2020/6/28 15:42
* rsa 基本算法
*/
public class SimpleRSA {
// 加密算法
public static long rsa(int baseNum, int key, long message) {
if (baseNum < 1 || key < 1) {
return 0L;
}
//加密或者解密之后的数据
long rsaMessage = 0L;
//加密核心算法
rsaMessage = Math.round(Math.pow(message, key)) % baseNum;
return rsaMessage;
}
public static void main(String[] args) {
//基数
int baseNum = 3 * 11;
//公钥
int keyE = 3;
//密钥
int keyD = 7;
//未加密的数据
long msg = 30L;
//加密后的数据
long encodeMsg = rsa(baseNum, keyE, msg);
//解密后的数据
long decodeMsg = rsa(baseNum, keyD, encodeMsg);
System.out.println("加密前:" + msg);
System.out.println("加密后:" + encodeMsg);
System.out.println("解密后:" + decodeMsg);
}
}