Day_26，动态规划

何为动态规划

动态规划是用来解决子问题重叠的情况，对于这部分重叠的问题，可以预先创建一份表，对应保存着这些子问题的解，在遇到重叠的子问题的时候就直接读表求解而不用重新计算，以此减少运行时间。

下面将用一个简单的问题引入动态规划算法及其优势

切割钢管

如上表所示，钢管长度对应的价格如上表，现在有一根长度为 n 的钢管，Q：如何切割这根长度为n的钢管使得收益最高？
分析：
①长度为n的钢管有 2^n-1 种切割方式（长度为n的钢管有n-1个切割点，每个点有切和不切两种选择）
②当第一次切割的时候，上述问题转为 r_n = max{p_i ；r₁+r_n-1 ；r₂+r_n-2…r_n-1+r₁}，其中r_n为长度为n的钢管的最高收益，p_i为不切割时候的售价，后面分别表示为切割成 i= 1、2、3…n-1段中两段的价格，取其中的最大值。
③第一次切割结束后，我们将切割后的两根钢管看成两个单独的子问题，每个子问题继续沿用上述方法求解，总问题的解则为这两个子问题最优解的组合。
④通过上述②③的循环将问题分割成数量越来越多且规模越来越小的子问题。问题的最优解则由这些子问题的最优解组成。

r_n = max{p_i ；r₁+r_n-1 ；r₂+r_n-2…r_n-1+r₁} 也可以描述为

即分解出一段最优解p_i以及一段切割的钢管r_n-i

非动态规划时的代码

#include 
#include 
#include 
using namespace std;

int max(int num1, int num2)
{
   if (num1 > num2)
      return num1;
   else
      return num2;
}

int CutRod(int price[],int n)
{
    int maxPrice = -1;
    if (n==0)
        return 0;
    else
    {
        for (int i=1;i<=n;i++)
        {
            maxPrice = max(maxPrice,price[i-1]+CutRod(price,n-i));
        }
    }
    return maxPrice;
}

int main()
{
    int rodLength = 10;
    int priceList[40] = {1,5,8,9,10,17,17,20,24,30,35,40,44,50,56,58,62,65,73,80,82,92,97,104,109,115,120,124,130,133,139,141,144,149,155,159,164,165,170,180};
    int price = CutRod(priceList,rodLength);
    cout<<"rodLength = "<<rodLength<<" price = "<<price;
}

改变上述 rodLength 的值分别为10、20、30、31、32，分别得到下面5张图的结果：





从上述结果可以明显的看出，运行时间在爆炸式增长，从下图我们容易得出原因

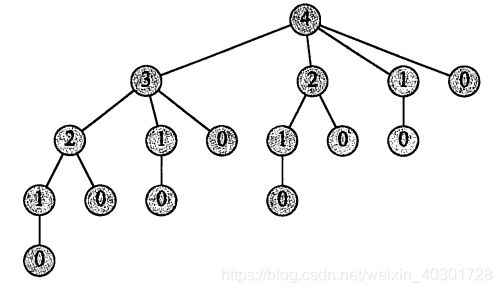
以n=4为例，可以看出，整个计算过程中重复计算了大量的 n = 0、1、2的结果，随着 n 的增大，这类的重复问题会爆炸式增长，导致运行时间爆炸式变长。

动态规划可以很好的解决这类问题，我们可以将计算过程中得到的 n = 0、1、2的结果保存在一份表中，当再次遇到的时候直接读表，这就省去了大量的计算时间

使用动态规划的代码

#include 
#include 
#include 
using namespace std;

int max(int num1, int num2)
{
   if (num1 > num2)
      return num1;
   else
      return num2;
}

//自顶向下的计算方法
void InitArray(int *a,int length)
{
    for (int i=0;i<length;i++)
    {
        a[i] = -1;
    }
}

int CupRodUpToDown(int *price,int n,int *a)
{
    int memoPrice = -1 ;
    if (a[n]>=0)
        return a[n];
    if (n == 0)
    {
        memoPrice = 0;
    }
    else
    {
        for (int i =1;i<=n;i++)
        {
            memoPrice = max(memoPrice,price[i-1]+CupRodUpToDown(price,n-i,a));
        }
    }
    a[n] = memoPrice;
    return memoPrice;
}

int main()
{
    int memo[41] = {};
    int rodLength = 32;
    int priceList[41] = {1,5,8,9,10,17,17,20,24,30,
                        35,40,44,50,56,58,62,65,73,80,
                        82,92,97,104,109,115,120,124,130,133,
                        139,141,144,149,155,159,164,165,170,180,189};
    InitArray(memo,sizeof(memo) / sizeof(*memo));
    int price = CupRodUpToDown(priceList,rodLength,memo);
    cout<<"rodLength = "<<rodLength<<" price = "<<price<<endl;
    for (int i=0;i<sizeof(memo) / sizeof(*memo);i++)
    {
        cout<<memo[i]<<" ";
    }
}
//自底向上的计算方法
void InitArray(int *a,int length)
{
    for (int i=0;i<length;i++)
    {
        a[i] = -1;
    }
}

int CupRodDownToUp(int *price,int n)
{
    int memo [41] = {};
    InitArray(memo,sizeof(memo) / sizeof(*memo));
    memo[0] = 0;
    //这里其实和冒泡排序很像
    //先计算出可能会用到的底部结果
    for (int i=1;i<=n;i++)
    {
        int memoPrice = -1;
        for (int j=1;j<=i;j++)
            memoPrice = max(memoPrice,price[j-1]+memo[i-j]);
        memo[i] = memoPrice;
    }
    return memo[n];
}

int main()
{
    int rodLength = 32;
    int priceList[41] = {1,5,8,9,10,17,17,20,24,30,
                        35,40,44,50,56,58,62,65,73,80,
                        82,92,97,104,109,115,120,124,130,133,
                        139,141,144,149,155,159,164,165,170,180,189};

    int price = CupRodDownToUp(priceList,rodLength);
    cout<<"rodLength = "<<rodLength<<" price = "<<price<<endl;
}



//重新更改后的可以得出切割长度分别为多少
void InitArray(int *a,int length)
{
    for (int i=0;i<length;i++)
    {
        a[i] = -1;
    }
}

int result [41] = {};//记录钢管切割左段的长度
int CupRodDownToUp(int *price,int n)
{
    int memo [41] = {};
    InitArray(memo,sizeof(memo) / sizeof(*memo));
    InitArray(result,sizeof(result) / sizeof(*result));
    memo[0] = 0;
    result[0] = 0;
    for (int i=1;i<=n;i++)
    {
        int memoPrice = -1;
        for (int j=1;j<=i;j++)
            if (memoPrice < price[j-1]+memo[i-j])
            {
                memoPrice = price[j-1]+memo[i-j];
                result[i]=j;//result[n]=左段的长度j
            }
        memo[i] = memoPrice;
    }
    return memo[n];
}

int main()
{
    int rodLength = 10;
    int priceList[41] = {1,5,8,9,10,17,17,20,24,30,
                        35,40,44,50,56,58,62,65,73,80,
                        82,92,97,104,109,115,120,124,130,133,
                        139,141,144,149,155,159,164,165,170,180,189};

    int price = CupRodDownToUp(priceList,rodLength);
    cout<<"rodLength = "<<rodLength<<" price = "<<price<<endl;
    for (int i=0;i<=rodLength;i++)
    {
        cout<<i<<" "<<result[i]<<endl;
    }
}

计算结果如下图，（1）为自顶向下 （2）自底向上 （3）含钢管切割信息的解

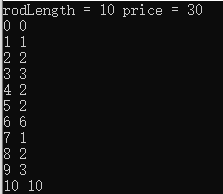
**自顶向下及自底向上的对比：**自顶向下调用了较多的递归函数，因此运行时间上要长一些，并且两者的时间复杂度是差不多的，仅仅是系数有所区别。

总结：可以看出，当我们引入 “memo” 记录已经计算过的结果时，运行速度明显减少加粗样式**

下面分析一下上面三种方法的运行时间

递归算法:
$$\begin{array}{r}T(n)=1+\sum _{j=0}^{n-1}T(j)\\ =1+\sum _{j=0}^{n-1}{2}^j\\ =1+(2^n-1)\\ =2^n.\end{array}$$
自顶向下：
通过观察式子，我们知道当求解memo中存在的问题时，递归会直接返回结果，所以实际上对每个子问题只求解了一次，因此我们实际上只求解了 0~n 的子问题，又因为自顶向下的循环里面每次都会循环 n次，因此运行时间是
$$T(n)=\sum _{j=0}^{n}n=a_{1}n+\frac{n(n-1)d}{2}=n+\frac{n(n-1)}{2}=\frac{n^2+n}{2}$$
自底向上：
通过观察可以知道，循环的过程其实是个等差数列，公差为1
$$T(n)=a_{1}n+\frac{n(n-1)d}{2}=n+\frac{n(n-1)}{2}=\frac{n^2+n}{2}$$

通过上述计算也可以明显看出动态规划对运行时间有着很大的提高！