UWB定位实验 - 晶振时钟频率偏移测试
摘要
基于UWB时钟模型，实验主要关注UWB模块相对系统参考时钟的归一化频率，测试在不同的发送时间间隔下归一化频率偏差随时间的变化关系，以及相邻时刻的归一化频率的差值变化和发送时间间隔的关系。
晶振时钟测试原理
基于在UWB系统时钟模型中的推导，对UWB模块来说，包含晶振误差和天线延迟误差的总体时钟模型近似为：
t M = α f M t + β M t^M = \alpha_f^M t + \beta^M tM=αfMt+βM
其中 α f M \alpha_f^M αfM为该模块相对系统参考时钟的归一化频率，其值的大小约等于1，而 β M \beta^M βM则是该模块相对系统参考时钟的时间偏移量。
假定UWB时钟参考基站按一定的间隔大小连续发送blink数据包，记该时钟参考基站的blink的发送时间为：
t 0 , t 1 , t 2 , ⋯ t_0, t_1, t_2, \cdots t0,t1,t2,⋯
而UWB模块M则不停接收来自该时钟参考基站的blink数据，记UWB模块M的对每一个blink的接收时间为：
t 0 M , t 1 M , t 2 M , ⋯ t_0^M, t_1^M, t_2^M, \cdots t0M,t1M,t2M,⋯
根据UWB模块的时钟模型有如下关系：
t k M = α f M t k + β M t_k^M = \alpha_f^M t_k + \beta^M tkM=αfMtk+βM
对UWB模块M两个相邻时刻i,j的数据进行相减，有：***[相邻时刻意味着， α f ≃ α f ( t i ) ≃ α f ( t j ) , β ≃ β ( t i ) ≃ β ( t j ) \alpha_f \simeq \alpha_f(t_i) \simeq \alpha_f(t_j), \beta \simeq \beta(t_i) \simeq \beta(t_j) αf≃αf(ti)≃αf(tj),β≃β(ti)≃β(tj)]***
t j M − t i M = ( α f M t j + β M ) − ( α f M t i + β M ) ≃ α f M ( t j − t i ) t_j^M - t_i^M = (\alpha_f^M t_j + \beta^M) - (\alpha_f^M t_i + \beta^M) \simeq \alpha_f^M (t_j - t_i) tjM−tiM=(αfMtj+βM)−(αfMti+βM)≃αfM(tj−ti)
即在两个相邻时刻i,j间，UWB模块M的归一化频率可近似为，
α f M ≃ t j M − t i M t j − t i \alpha_f^M \simeq \frac{t_j^M - t_i^M}{t_j - t_i} αfM≃tj−titjM−tiM
测试实验结果
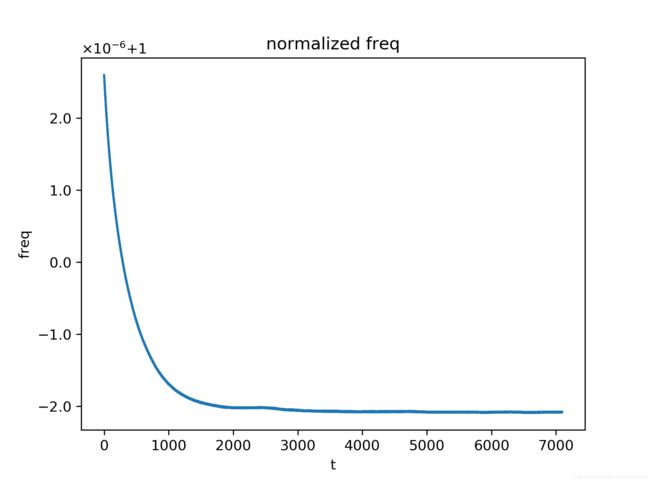
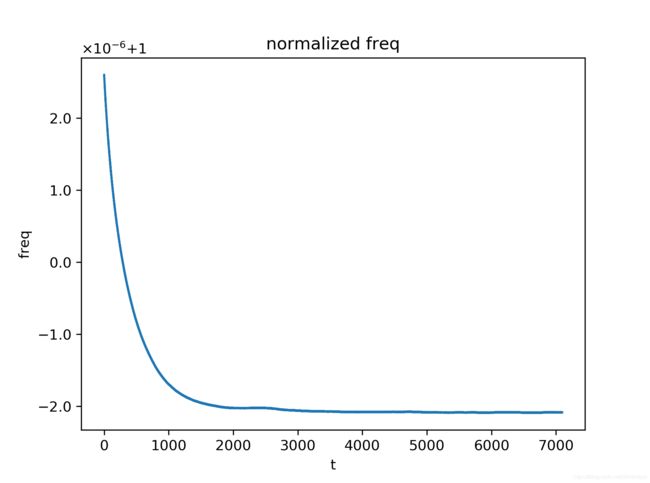
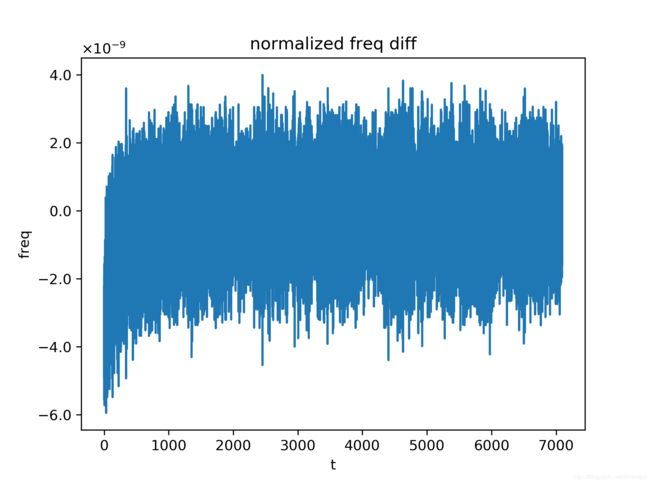
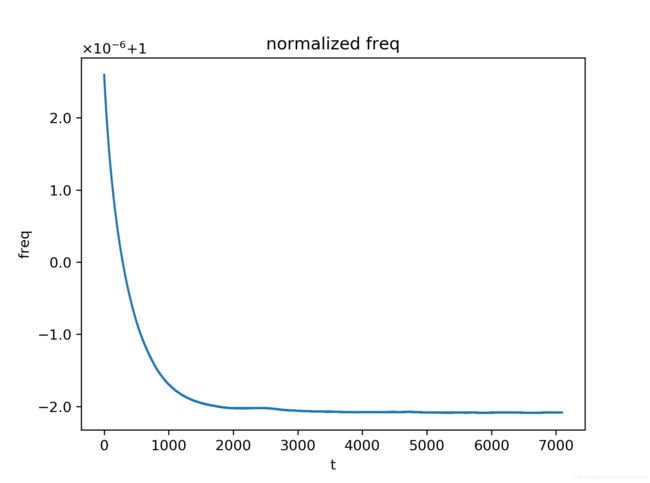
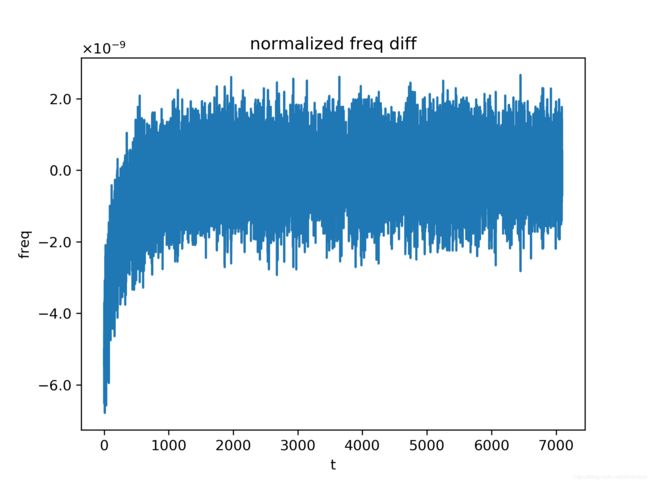
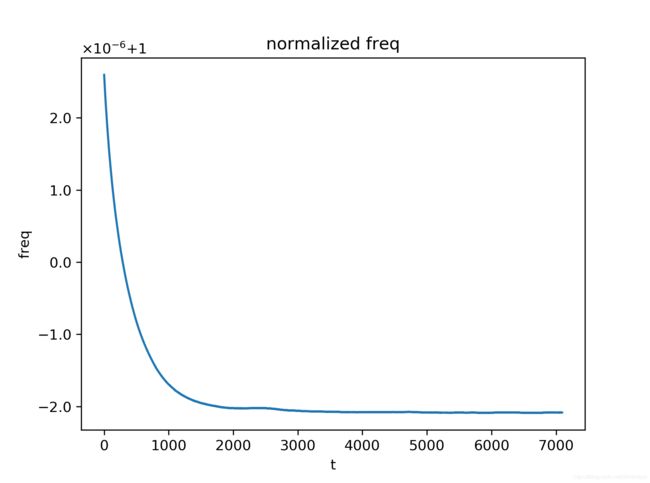
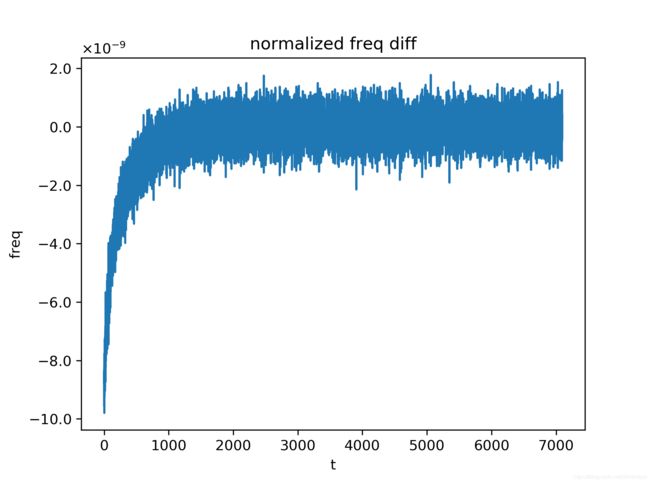
实验中设置不同的时钟参考基站发送blink数据的时间间隔，分别为50ms，100ms，200ms，300ms，500ms，总计进行5次的数据分析。实验结果主要关注在UWB模块M相对时钟参考基站的归一化时钟频率 α f M \alpha_f^M αfM随时间的变化特性，包括 α f M \alpha_f^M αfM随时间变化曲线，以及相邻时刻 α f M \alpha_f^M αfM的差值随时间变化的曲线。
-
blink时间间隔：50ms
-
blink时间间隔：100ms
-
blink时间间隔：200ms
-
blink时间间隔：300ms
-
blink时间间隔：500ms
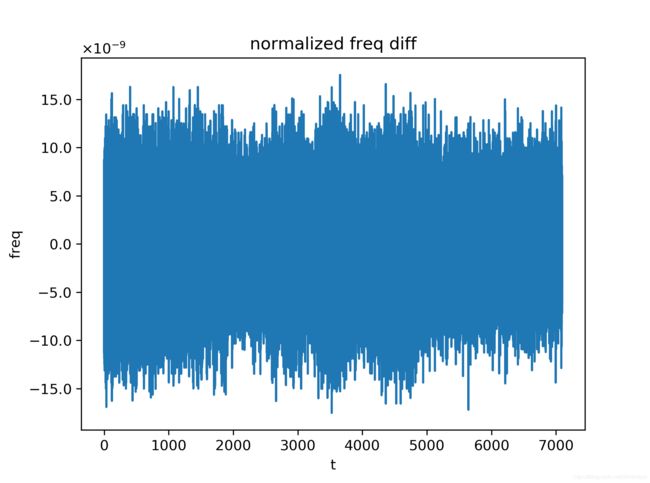
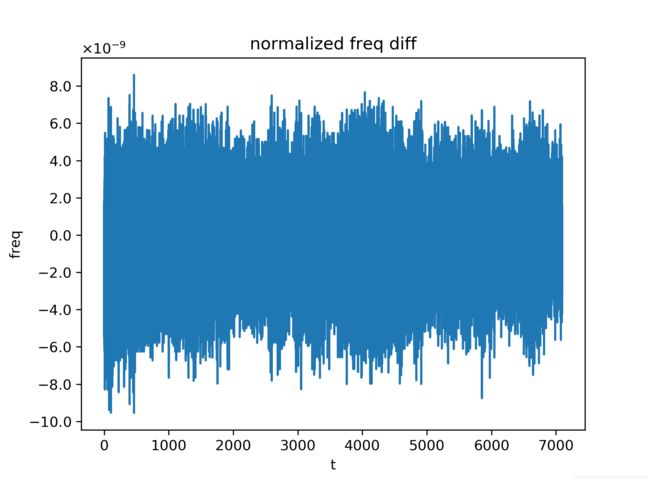
从实验结果可以看出，在不同的blink数据发送时间间隔下， α f M \alpha_f^M αfM随时间的变化趋势是几乎一致的，而相邻时刻 α f M \alpha_f^M αfM的差值波动则随blink数据发送时间间隔的增大而减小，这可归结为对 α f M \alpha_f^M αfM的近似中，端点误差的影响被较大的间隔时间所平滑掉了，具体地说，由
α f M ≃ t j M − t i M t j − t i \alpha_f^M \simeq \frac{t_j^M - t_i^M}{t_j - t_i} αfM≃tj−titjM−tiM
假定在端点时刻 t i t_i ti， t j t_j tj时， t j M t_j^M tjM， t i M t_i^M tiM的接收误差分别为： e j e_j ej， e i e_i ei，该误差主要与UWB模块M本身的制造特性以及环境中其它无线信号的干扰有关，在整个实验过程中，可认为其噪声特性几乎稳定不变，并进一步假定其为高斯白噪声，即 e j ∼ N ( 0 , σ ) , e i ∼ N ( 0 , σ ) e_j\sim\mathcal{N}(0, \sigma), e_i\sim\mathcal{N}(0, \sigma) ej∼N(0,σ),ei∼N(0,σ)，有，
α f M ≃ t j M − t i M t j − t i = t j M − e j − t i M + e i t j − t i = t j M − t i M t j − t i − e j − e i t j − t i \begin{aligned} \alpha_f^M &\simeq \frac{t_j^M - t_i^M}{t_j - t_i} \\ &= \frac{t_j^M - e_j - t_i^M + e_i}{t_j - t_i} \\ &= \frac{t_j^M - t_i^M}{t_j - t_i} - \frac{e_j - e_i}{t_j - t_i} \\ \end{aligned} αfM≃tj−titjM−tiM=tj−titjM−ej−tiM+ei=tj−titjM−tiM−tj−tiej−ei
从而 α f M \alpha_f^M αfM的误差为 e j − e i t j − t i \frac{e_j - e_i}{t_j - t_i} tj−tiej−ei，该误差均值和标准差分别为
{ μ = μ ( e j − e i t j − t i ) = 0 σ = σ ( e j − e i ∣ t j − t i ∣ ) = 2 σ ∣ t j − t i ∣ \left\{ \begin{aligned} \mu &= \mu\left(\frac{e_j - e_i}{t_j - t_i}\right) = 0 \\ \sigma &= \sigma\left(\frac{e_j - e_i}{|t_j - t_i|}\right) = \frac{\sqrt{2}\sigma}{|t_j - t_i|} \\ \end{aligned} \right. ⎩⎪⎪⎪⎨⎪⎪⎪⎧μσ=μ(tj−tiej−ei)=0=σ(∣tj−ti∣ej−ei)=∣tj−ti∣2σ
由上述分析可得，相邻时刻 α f M \alpha_f^M αfM的差值波动大小随blink数据发送时间间隔的增大而减小，验证了端点误差的影响被较大的间隔时间所平滑的猜想。
无线定位导航技术交流
目前在做用于机器人和人机协作的UWB定位导航方案，开发过程中遇到各种困难，查阅了大量技术文档，论文资料，国内外相关论坛等，体会到没有一个专注于无线定位技术和应用的技术论坛、交流区、交流群可能使得很多项目的开发在初期就可能难以进行，因而希望构建这个交流群能够聚集从事无线定位技术的人员交流想法经验等。
以下是我们项目的商业推广：
