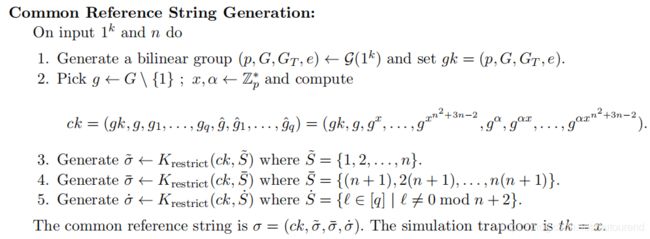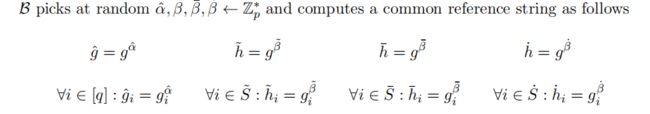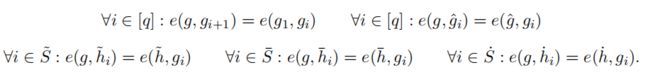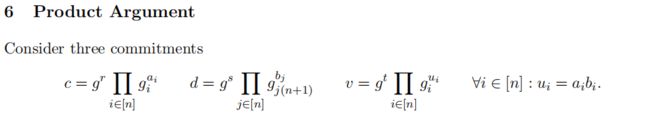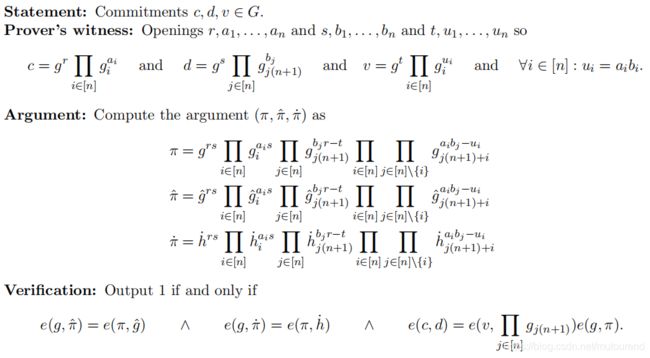Short Pairing-based Non-interactive Zero-Knowledge Arguments
1. 背景知识
Groth 2010年论文《Short Pairing-based Non-interactive Zero-Knowledge Arguments》
- 使用了common reference string，需要trusted setup，且common reference string很大【可优化，见论文第九章】;
- Sub-linear size non-interactive zero-knowledge arguments，若common reference string足够大的化，proof可为a constant number of group elements；
- Public verification;
- 基于pairing-based cryptography;
- 没有使用Fiat-Shamir假设or random oracles，而使用了q-CPDH(q-power knowledge of exponent assumption)和q-PKE(q-computational power Diffie-Hellman assumption)。
Zero-knowledge proofs有三个主要特性： - Completeness: The prover can convince the verifier if the prover knows a witness testifying to the truth of the statement.
- Soundness: A malicious prover cannot convince the verifier if the statement is false. Soundness可分为computational soundness（protect against polynomial time cheating provers，computationally sound proofs又可称为arguments）和statistical or perfect soundness（此时，even an unbounded prover cannot convince the verifier of a false statement）。
- Zero-knowledge: A malicious verifier learns nothing except that the statement is true. 也可分为computational zero-knowledge和statistical or perfect zero-knowledge。
基于标准密码学假设的NIZK proofs在实际使用是效率低下并不实用，为了解决效率问题：
1）应用密码学专家引入了Fiat-Shamir heuristic for transforming public-coin interactive zero-knowledge proofs into NIZK arguments by using a cryptographic hash-function to compute the verifier’s challenges. 但是Groth认为实际中，random oracle model安全并不意味着有相应的hash function能实际达到安全。所以在该论文中，Groth介绍了一种新的不基于random oracle model但仍然可以实现sub-linear size NIZK arguments的方法，尽管其效率不如基于Fiat-Shamir heuristic的NIZK argument。
[The Fiat-Shamir heuristic can give very efficient NIZK arguments that are secure in the random oracle model [BR93], where the cryptographic hash-function is modeled as a random function. It is for instance possible to use the Fiat-Shamir heuristic to transform sub-linear size interactive public-coin zero-knowledge arguments [Kil92] into sub-linear size non-interactive zero-knowledge arguments [Mic00]. Unfortunately, there are several examples of protocols that are secure in the random oracle model, but do not have any secure standard model instantiation no matter which hash-function is used [CGH98,CGH04,MRH04,BBP04,Nie02]. Particularly relevant here is Goldwasser and Kalai’s [GK03] demonstration of a signature scheme built from a public-coin identification scheme that is secure in the random oracle model but insecure in real life. While it is possible that the Fiat-Shamir heuristic is secure for “natural” protocols, it is worthwhile to investigate alternative approaches.]
2）为了解决传统NIZK proof的效率问题，可采用non-interactive designated verifier proofs，而不是public verifiable。但是在需要环签名、群签名等场景的应用中，designated verifer设计并不适用。
有一个二进制circuit C，其内部均为与非门组成 a = ~(a ^ b)，存在某个输入，使得最终Circuit C的输出为1。
在有限域内，对n个值进行commit成a constant number of group elements来实现length-reducing。同时所采用的commitment scheme应具有同态性，可对committed values证明如下属性：
该论文中，采用的commitment scheme为Pedersen commitment scheme，其中commitment key为 ( g , g x , g x 2 , … , g x q ) (g,g^x,g^{x^2},…,g^{x^q}) (g,gx,gx2,…,gxq)，对 ( a 1 , a 2 , … , a q ) (a_1,a_2,…,a_q) (a1,a2,…,aq)commit a single group element为 g r ∏ i = 1 q ( g x i ) a i g^r\prod_{i=1}^{q}(g^{x^i})^{a_i} gr∏i=1q(gxi)ai。采用这种commitment scheme的优点是，其discrete logarithm是一个简单的多项式 r + ∑ i = 1 q a i x i r+\sum_{i=1}^{q}a_ix^i r+∑i=1qaixi，当pair two commitments with each other时，得到的是a product of two polynomials in exponent（可通过合理组合表达多项式的系数，使得乘积后的一些系数可cancel掉，来达到简洁表达entry-wise product和permutation non-interactive argument的目的）。By taking appropriate linear combinations over products of polynomials, we can express entry-wise products and permutations as equations over the coefficients of these polynomials. The q-CPDH assumption then allows us to conclude that these coefficients are identical and therefore the committed values satisfy an entry-wise multiplication relationship or a permutation relationship to each other.
对 ( a 1 , a 2 , … , a q ) (a_1,a_2,…,a_q) (a1,a2,…,aq)commit为 c = g r ∏ i = 1 q ( g i ) a i c=g^r\prod_{i=1}^{q}(g_i)^{a_i} c=gr∏i=1q(gi)ai【其中， g i = g x i g_i=g^{x^i} gi=gxi】，同时，考虑到在3SAT证明时，需要能够extract the committed values a 1 , a 2 , … , a q a_1,a_2,…,a_q a1,a2,…,aq，对此，额外增加一个关联的commitment c ^ = g ^ r ∏ i = 1 q ( g i ^ ) a i \hat{c}= \hat{g}^r\prod_{i=1}^{q}(\hat{g_i})^{a_i} c^=g^r∏i=1q(gi^)ai【其中， g ^ = g α , g i ^ = ( g i ) α \hat{g}=g^{\alpha},\hat{g_i}=(g_i)^{\alpha} g^=gα,gi^=(gi)α】，整个 ( c , c ^ ) (c,\hat{c}) (c,c^)即称为knowledge commitment.
Restriction Argument：
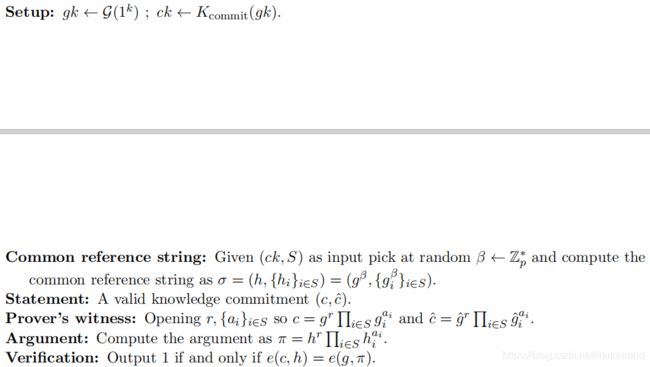
2. Hadamard Product argument
注意：for i ∈ [ n ] , g x i ( n + 2 ) i \in [n], g^{x^{i(n+2)}} i∈[n],gxi(n+2)应不包含在CRS中 ，否则dishonest prover可以作弊。具体可看Lipmaa 2012年论文《Progression-Free Sets and Sublinear Pairing-Based Non-Interactive Zero-Knowledge Arguments 》
- 其中 π ^ \hat{\pi} π^【knowledge commitment】和 π ˙ \dot{\pi} π˙【restriction argument】用于辅助证明prover确实知道 π \pi π对应的opening ( z , { z l } l ∈ S ˙ ) (z,\{z_l\}_{l\in \dot{S}}) (z,{zl}l∈S˙) restricted in S ˙ \dot{S} S˙。
- 其中2个commitment c 和 v c和v c和v 对应 S ~ \tilde{S} S~，1个commitment d d d 对应 S ˉ \bar{S} Sˉ。 S ~ \tilde{S} S~和 S ˉ \bar{S} Sˉ之间的commitment可以直接相互转换。若已知 v v v【对应 S ~ \tilde{S} S~】和 d d d【对应 S ˉ \bar{S} Sˉ】，可认为 v v v为 d d d和 c = ∏ i ∈ [ n ] g i c=\prod_{i\in [n]}g_i c=∏i∈[n]gi【此处， c c c可认为是 ( 1 , . . . , 1 ) (1,...,1) (1,...,1)的commitment】的product commitment。
3. product argument作为bits证明
上述的product argument可用于证明 c c c为bits ( a 1 , a 2 , . . . , a n ) (a_1,a_2,...,a_n) (a1,a2,...,an) 的commitment，方法为：
构建commitment d d d具有与 c c c相同的元素，证明 c c c和 d d d的product commitment仍为 c c c，则有 a i = a i 2 a_i=a_i^2 ai=ai2，从而可证明 a i ∈ { 0 , 1 } a_i\in\{0,1\} ai∈{0,1}。
4. Permutation Argument
证明 b ⃗ \vec{b} b为 a ⃗ \vec{a} a的排列组合，具体可表述为：
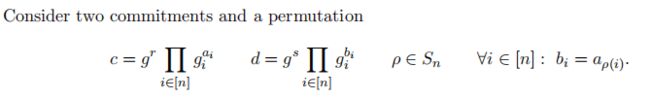
进一步可转换为证明：
5. CIRCUITSAT argument——Circuit Satisfiability Constant Size NIZK Argument
6. vector完全相同证明
证明两组向量 a ⃗ \vec{a} a和 b ⃗ \vec{b} b完全相同，可表述为：
