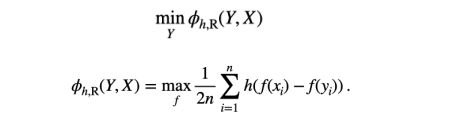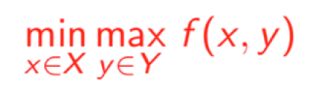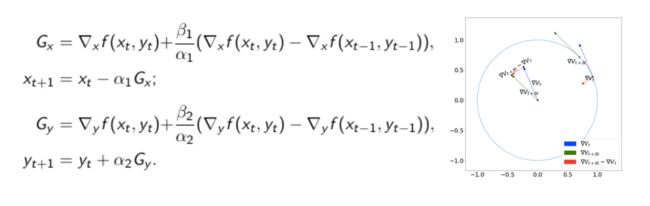重构广义应用数学:人工智能,数学发展的重大机遇
2020 北京智源大会
本文属于2020北京智源大会嘉宾演讲的整理报道系列。北京智源大会是北京智源人工智能研究院主办的年度国际性人工智能高端学术交流活动,以国际性、权威性、专业性和前瞻性的“内行AI大会”为宗旨。2020年6月21日-24日,为期四天的2020北京智源大会在线上圆满举办。来自20多个国家和地区的150多位演讲嘉宾,和来自50多个国家、超过50万名国内外专业观众共襄盛会。
在人工智能发展的今天,数学家被赋予了新的使命。
作为自然科学的基石,在任何一门科学发展成熟的时候,对其进行抽象、定义以及严格证明,都是数学发挥功力的时刻。人工智能进入以深度学习为代表的第三波爆发期后,迄今为止,大多数工作都还主要是凭借计算机科学家们的经验、灵感,以工程的思维来推动。近几年来有不少数学家已经开始认识到,对人工智能数理基础的研究或许将带来数学的又一春天。传统的数学(特别是统计)主要是从线性模型做起,直接分析优化,不用考虑学习;而深度学习在数学上本质上则是非凸的,学习策略影响学习结果。如何刻画这种学习?如何为以深度学习为代表的机器学习技术建立坚实的数理基础?对深度学习的研究,让原来局限在一个小圈子里的数学家们也有了很多机会,与计算机学家、人工智能学家、物理学家、脑科学家、计算神经科学家等坐在一起,共商人工智能的科学之本。与人工智能的交叉,将给数学界带来新的灵感。
当前,已经有不少数学家开始研究机器学习问题,例如 GAN的数学描述即优化问题,双下降问题,极大极小优化问题,因果推断等。这些研究已取得或大或小的进展,但,正如智源研究院数理基础方向首席科学家、中国科学院院士、北京大学教授张平文所言:“人工智能的数理基础,还不是一个成熟的、被明确定义的领域,人工智能数理基础研究的领导者还没有产生;正是因为这样,广大的青年学者现在还有很大的机会。”
正是基于此种考虑,北京智源人工智能研究院在2019年初,首次建立了「人工智能的数理基础」这一重大研究方向,将相关的研究者汇聚在一起,共同推动这一领域的发展。
在 6 月21-24 日举办的智源大会上,由担任「智源研究院数理基础方向首席科学家」职位的张平文院士主持召开了“人工智能的数理基础专题论坛”。在论坛上,首先由 4 位国内外数理基础研究学者分享了他们在GAN、双下降、极大极小优化、因果推理等方面的研究成果;随后,8 位数学家共同回顾并探讨了人工智能基础理论在近几年取得的重要进展、当前最核心的挑战以及未来潜在的新思路和方向。
主席:张平文
时间:2020年6月21日
报告嘉宾:孙若愚,Johannes Schmidt-Hieber,戴彧虹,林伟
参与讨论嘉宾:张平文,张志华,史作强,董彬,朱占星,朱宏图,季春霖,邓柯
整理:智源社区 贾伟,范歆琦, 肖辉, 吴继芳
审核:戴彧虹,孙若愚, 夏壁灿, 朱占星,史作强,张志华, 张平文,董彬,李铁军,林伟
一、演讲核心要点概述
1、两行代码,改变 GAN 的全局优化
演讲嘉宾:孙若愚,University of Illinois Urbana-Champaign
主题:Towards Better Global Landscape of GAN: How Two Lines of Code Change Makes a Difference
生成对抗网络(Generative Adversarial Network, GAN)自2014年由Ian Goodfellow 等人提出,如今已经六年。尽管已经得到大量的关注和应用,但很遗憾,人们对GAN的认识还相当有限。其中一个挑战是便是:GAN 优化是一个非凸非凹的极小极大问题,这使得理论分析非常困难。数学优化的理论分析一般分为几个步骤(如下图所示):局部最优好不好,算法是否收敛到局部最优,收敛速度多快。他们的目标是从最基础的步骤开始分析GAN:是否真的存在坏的局部最优?如果存在,能否修改?
简单来说,GAN 是一种生成模型,它能够根据已有的数据样本(比如1000张人脸图片)来产生新的数据(比如全新的人脸图片)。它由一个生成器网络和一个判别器网络组成。生成器网络 G 直接生成样本,其对手判别器网络 D 试图区分从训练抽取的样本和从生成器抽取的样本,最终当判别器无法分辨它们的时候,便达到了生成器和判别器的均衡。GAN的模型一般写成一个最大最小优化问题,原始的GAN模型叫做JS-GAN:
Goodfellow等人的原始文章证明了 是一个凸函数。但是这个证明并没有利用GAN的结构,因为任何一个概率密度函数(probabilistic density function)的线性函数都是凸函数。
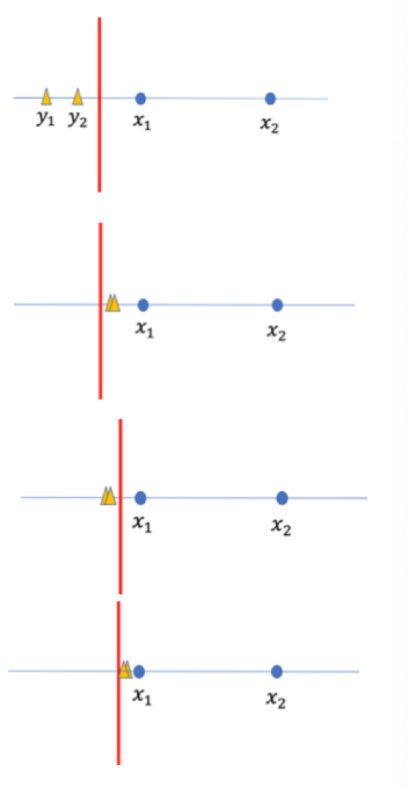
孙若愚和合作者 (Tiantian Fang, Alex Schwing) 考虑了GAN的经验损失目标函数(而不是传统的概率密度的函数),并证明了JS-GAN 会存在许多坏的局部严格最优点 (Sub-Optimal Strict Local-Min),并由此会导致模式坍塌 (Mode Collapse)。为了帮助读者直观的理解这个结论,他们考虑了一个简单的两点分布。如下图所示,x 是真实数据,y 是生成的数据,红线表示判别器。刚开始,判别器能够很轻松的分别 x 和 y 。然后,y 会向右移动,直到判别器不能够区分他们。但是,这种使用了 JS 作为优化目标的GAN,会使得生成的点集中在第一个 x 点附近,这就是模式坍塌。
为了修补JS-GAN的缺陷,孙若愚和合作者分析了R-GAN(Relativistic GAN),该模型能够耦合生成样本和真实样本。R-GAN的优化模型可以写成:
其中一个特例是h为Logistic函数,这个模型叫做RS-GAN (relativistic standard GAN)。他们严格证明了R-GAN的损失函数满足全局最小可达(Global Min Reachable, GMR)的性质:从任意点到全局最小点存在一条非增的连续路径。这个性质说明R-GAN不存在坏的局部严格最优点。这个定理只需要对h有一些简单的要求 (最大值是0, 凹函数), 其中RS-GAN也满足这个定理的条件。
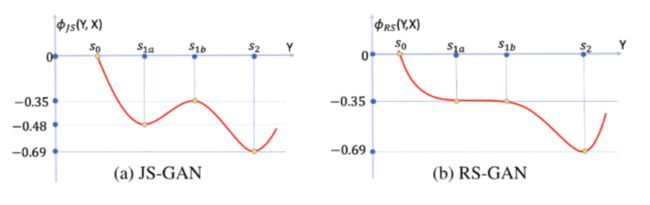
他们也将landscape进行可视化,来说明RS-GAN的平滑性。可以看到JS-GAN会有一个严格局部最优点(一个山谷),这个点对应于模式坍塌(见最右的图示例),但RS-GAN没有山谷,只有一个严格局部最优点。
那么如何实现 RS-GAN 呢?只需要对原本的JS-GAN做如下两行的更改即可(PyTorch代码):
之前其他团队的实验结果已经说明了R-GAN的有效性,比如超分辨率的一个获奖模型ESR-GAN就使用了R-GAN; 最近的realnessGAN也用了R-GAN。孙若愚和合作者的实验结果进一步验证了RS-GAN在大多数情况下有着更优秀的表现,并说明了RS-GAN确实有更好的全局最优性质。
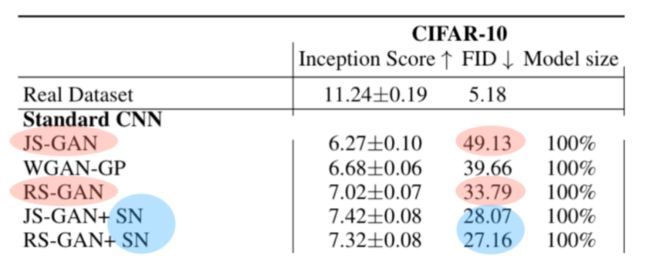
在不使用Spectral Normalization(SN)的情况下,可以看到RS-GAN比JS-GAN在CIFAR-10数据集上的表现要优秀,它的FID值只有33.79,而JS-GAN高达49; 这里FID (Frechet Inception Distance) 是计算真实图像和生成图像的特征向量之间距离的一种度量,越小越好。在使用了SN之后,JS-GAN和RS-GAN的差距变小了,因为SN也起到了提高全局优化性质的作用。为了说明在使用SN的情况下RS-GAN仍然有更好的优化性质,他们预测在更窄的网络上,RS-GAN和JS-GAN的差距会变大,并通过CIFAR10和STL的实验验证了这个预测(FID差距为2到5个点)。
另外一个预测是存在一个初始点,RS-GAN和JS-GAN的差距非常大。在MNIST他们找到了这样的初始点,使得两者的差距可以达到30 FID点数以上,验证了这个猜测。这也进一步验证了他们的理论: RS-GAN比JS-GAN有着更好的全局优化性质。
2、双下降:存在一个普遍的下界,任何算法都不能避免
演讲嘉宾:Johannes Schmidt-Hieber
主题:Overparametrization and the Bias-Variance Dilemma
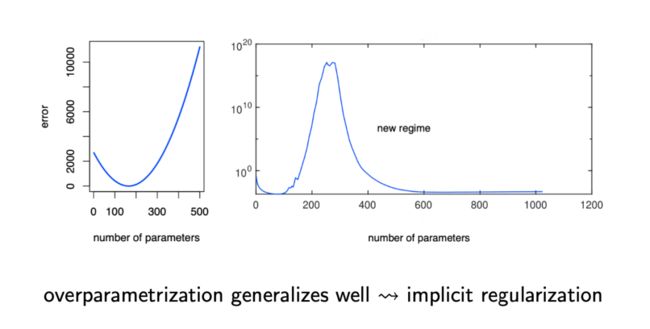
对于学习算法,我们通常会使用偏差(Bias)和方差(Variance)来解释算法的泛化性能。简单来讲,偏差度量了算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力;而方差度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。在一个实际系统中,偏差与方差往往是不能兼得的。模型过于简单时,容易发生欠拟合(Underfitting),即方差小而偏差太大;模型过于复杂时,又容易发生过拟合(Overfitting),即偏差小而方差太大。这便是偏差-方差权衡(Bias-Variance Trade-Off)。如下图左侧所示:
然而,对于以深度学习为代表的一些机器学习方法,却出现了违背直觉的现象,随着参数的增多,当出现过参数化的时候,算法的泛化性能却开始变好(如上图右侧)。
Schmidt-Hieber教授在这里考虑的问题并不是去解释为什么会出现这种现象,而是聚焦于另一个同样重要的问题:在原来的偏差-方差困境中,会存在一个下界;现在出现了二次下降,在新的区域(上右图的new regime)是否存在下界呢?还是说深度学习等机器学习算法可以避开这个困境?
他的结论是:存在一个普遍的下界,任何算法都不可能避免。他的研究结果表明,深度学习等过参数化方法并不能违反基本的统计学原理,解释“双下降”现象需要从新的思路考虑。
3、受限制极大极小优化问题的最优性条件
演讲嘉宾:戴彧虹
主题:Optimality Conditions for Constrained Minimax Optimization
戴彧虹研究员在报告中,分享了他们近期发布在arXiv上的一项研究工作《Optimality Conditions for Constrained Minimax Optimization》(arxiv.org/abs/2004.09730v1)。这项工作是基于Michael I. Jordan 等人对局部 Minimax 优化问题研究,而做出的进一步拓展,即约束条件下 的 Minimax 优化问题。
何为Minimax 优化问题呢?简单来讲,即有两个代理(Agent)来优化收益函数 f : X × Y → R,其中一个代理希望最小化函数,另外一个希望最大化函数,即
Minimax 优化问题不仅在鞍点问题、数值偏微分方程、等式约束优化等传统的数学研究中出现,近年来更是因对抗生成网络(GAN)、对抗学习、多智能体强化学习等而大热。
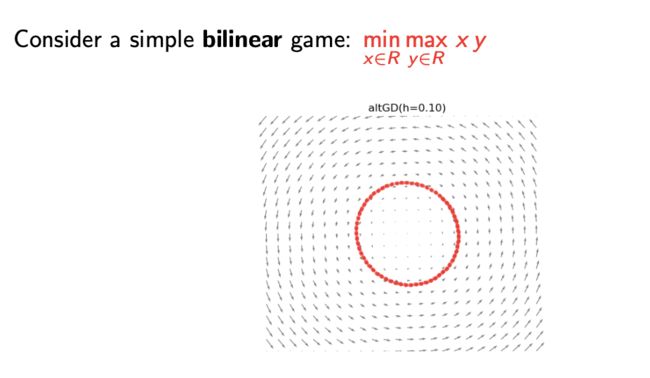
在实践中,Minimax优化通常是采用基于梯度下降/上升的方法来实现,即在 x 的梯度下降步和y的一些梯度上升步之间交替。但这种方法存在一个弊端,即不能保证收敛。如下图所示,
解决方法有很多中,基本思路便是加入高阶项。戴彧虹教授等人借鉴物理中的向心加速度的概念,提出了同时向心加速度(Simultaneous Centripetal Acceleration,SCA)方法,以期打破这种非收敛情形。如下图:
另一方面,尽管Minimax 优化已经研究多年,如何从数学角度如何准确描述Minimax优化却始终没有得到解决。
传统上,人们习惯用纳什均衡来描述,如下述定义
但这种定义存在极大的缺陷:它不能反映Min-Player和Max-Player的交替顺序,而在许多机器学习应用中,多是一个Player做出动作之后,另一个才继续,如此交替执行,![]() 和
和![]() 显然是不一样的。
显然是不一样的。
Michael I. Jordan 等人在2019年发表的论文《What is Local Optimality in Nonconvex-Nonconcave Minimax Optimization?》正是对这一问题的正视和解决。基于Stackelberg 均衡,他们提出了一个局域minimax点的定义:
受Jordan等人工作的启发,戴彧虹等人进一步提出了受限条件下的Minimax点定义。
受限条件为:
受限条件下的局部Minimax点的定义为
当满足一定推论时,受限条件下的Minimax问题可以在局部简化为如下问题,
通过低层级极大优化问题的雅可比唯一性条件和极大问题的强正则性Karush-Kuhn-Tucker conditions (KKT) 条件的分析,戴彧虹研究员等给出了约束Minimax优化问题局部Minimax点的必要最优性条件和充分最优性条件。这些条件如下:
必要最优条件——
二阶充分最优条件:
在强正则性下的一阶必要最优条件:
4、旧“工具”换新颜:因果推断提高算法可解释性
演讲嘉宾:林伟
主题:Instrumental Variables for Multiple Causal Inference: Old and New
近年来,包括图灵奖得主Judea Pearl在内的人工智能著名学者大力提倡因果推断研究,学界和业界普遍认识到因果推断的重要性。机器学习与因果推断的结合能否成为解决当前人工智能“黑箱”问题、提高模型和算法可解释性的有力工具?
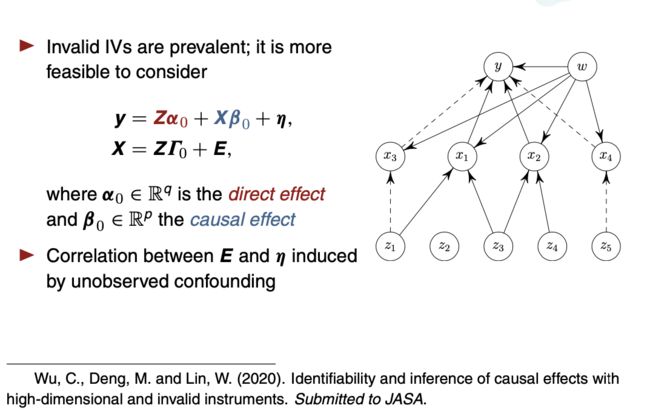
林伟研究员在报告中介绍了一种古老的因果推断方法——工具变量,并说明了这一经典因果推断方法是如何与现代机器学习方法结合,从而发挥出巨大威力的。他首先介绍了因果推断的基本困难,即存在未观测的混杂(Unobserved Confounding),使得因果效应的估计有偏。起源于1920年代计量经济学研究的工具变量(IV)方法可以解决这一问题,但经典工具变量方法要求三个有效性假设严格成立,难以迁移到现代的机器学习场景。
他接着指出,这三个假设中的两个,即工具变量与原因变量之间的关联已知,以及工具变量对结果变量没有直接效应的排他性假设,都可以在一定程度上放宽,从而更好地适用于机器学习任务。这一点在他与合作者关于工具变量模型识别性的理论研究中得到了证实。最后,在扩展的工具变量框架基础上,他详细介绍了几种新的因果推断方法,来提高人工智能算法的可解释性。
二、进展 | 挑战 | 展望
回顾:人工智能基础理论研究近年来取得了哪些重要进展?
机器学习视角——
朱占星:在基础理论方面,我觉得近几年进展比较多的包括以下四个方面:
1. 神经网络学习内在的工作机制是什么。近一两年大家研究比较多的是宽网络,即网络很宽时,神经网络的行为将是什么。大家发现这种学习很类似Kernel Learning。但也有人提出质疑,因为宽网络有很强的限制,和现在大家普遍用的深度网络并不一样,根据Kernel做出来的结果和我们深度学习做出来的结果仍然有很大差距。
2. 用新的视角来看神经网络。有人尝试利用物理中的平均场理论,把每个神经元视作一个粒子,根据中心极限定理,来分析神经网络整体的行为。
3. Double Descent问题。这种现象表明我们对传统的统计机器学习模型理解并不够透彻,例如前面Johannes对Bias-Variance Trade-Off的新理解。
4. 把机器学习看做一个动力系统。例如在训练的时候,把输入当做初始点,输出当做终点,训练时把步长不断缩小,这个过程可以看做一个连续ODE,因此我们可以用已有的数学方法来解决一些问题。
其他方面进展,我觉得都还并不很顺利,例如神经网络性能与Data之间的关系如何更好地进行数学上的刻画,如何De-Couple训练策略和训练模型之间的关系等。
张志华:我对这个问题的理解有两个方面。
首先,机器学习(特别是深度学习)现在发现了很多现象,对这些现象,数学上能够提供什么样的刻画?这方面确实发现了一些现象,例如双下降等,针对这些现象确实已经有一些工作,但这些工作都包含了太多的假设,这些假设与真实的机器学习过程有很大的差距。从数学上解决比较好的是GAN,原因在于:1)GAN本身数学的定义就比较清楚;2)我们对GAN做分析时,已经把“深度”(最难的一块儿)去掉了。因此对GAN的分析就比较漂亮。此外便是对Min-Max的研究,现在也是研究比较清楚的,这里也没有考虑“深度”。把“深度”加进去的研究,还处于起步阶段。
其次,人工智能的数学基础,并不一定是对人工智能的数学刻画,也可以是用数学的工具提出一些新的方法。例如无监督,如何从数学的角度,给我们一些启示,提出一些新的方法。这方面还是取得了一定的进展,包括统计的鲁棒性以及林伟讲的因果推理。我觉得这方面的进展还是比较清楚明晰的。
统计学习视角——
季春霖:从统计的角度,我关注的有几个方面,
1. 近似贝叶斯推断方面。近似贝叶斯推断最早是为了贝叶斯模型做后验分布计算,是一种替代蒙特卡洛计算的手段。最近近似贝叶斯推断与ML结合的比较多,也受到了很大的关注,特别是随机变分推断(Stochastic Variational Inference)能够处理复杂的、大规模的数据。其中VE应该是近似推断比较成功的例子。最近的一些突破主要是,近似推断尝试打破一些传统的基于模型假设的方法,提出了很多Model-Free的设想,在变分推断中会用到Proposal,这是一个分布,现在人们提出了很多不需要标准模型的Proposal,使得Proposal更加灵活,把原来用模型来算的Likelihood和Prior变成用统计量直接度量,或用GAN直接替代Likelihood和Prior等。
2. 另外关注比较多的是生成模型。其实GAN网络、VE都属于生成模型,能生成很多复杂的数据,这对传统的统计来说是一个技术的节约。VE本身还有一些基于统计模型的假设,它的重构损失等效于一个Likelihood,这就限制了模型的灵活性。而GAN用统计量直接生成数据和真实数据的距离,比较像统计学里的ABC计算。人们用不同的统计量去做GAN网络中的损失函数,尝试生成更好的效果。除了这些,还有尝试改变它的结构,引入条件或其他领域的先验知识,从而让生成模型更加逼真。
3. 统计量除了在GAN中用的比较多之外,它还被用在跨域的度量,例如用在Transfer Learning、特征解纠缠。但统计量不是On-Line的学习,因此我们应当关注利用On-Line的方法去解这种统计量,这样会更有助于在机器学习里面使用。
4. 数据生成。我们知道生成模型可以生成很多复杂数据,例如GAN,在最初生成图片等,可以满足大家的好奇心,但实际上现在更多的关注是用生成的数据提高监督学习或强化学习的性能,包括Few-Shot 或Zero-Shot Learning里面,利用生成数据提高监督学习的性能,都能达到很好的效果。这里值得关注的是,如何利用这个模型对数据里面的先验知识进行提取,并把这些先验知识转换成数据来喂给监督学习的模型,这还有很多创新的地方值得关注。
朱宏图:首先大家从理论上对Bias-Variance的研究还是不错的,也有很多人试图从逼近论的角度做深度学习的理论,不过还没有看到非常激动人心的东西,大家都还在尝试去做。
其次,大家尝试把统计模型和深度学习融合在一起去解决一些问题,因为本质上来说统计模型在解释性方面比较好。
另外,就是在强化学习中进行因果推断的研究。最近有越来越多的 IT公司开始做因果推断。我们最近也有一些研究,结果已经出来了,效果还不错。
应用数学视角——
史作强:前面几位老师已经说的很全面了,把我想说的基本已经说完了。我再补充一点,现在有些研究会把物理中的一些约束放到RNN 或Reinforcement Learning中,构建一些网络。例如在RNN中,加入某种能量或其他一些物理量,就可以利用数学上的一些理论来处理,例如常识的依赖性等克服梯度消失/爆炸现象。这可能也是现在应用那个数学研究的一个趋势,即:考虑传统上的一些物理模型,看是否对Deep Learning有一些启发。
董彬:近年来我们看到的一个趋势是,机理与数据的融合。不管你是Model Driven,还是Data Driven,我们在做的就是把基于数据和基于我们已知的机理与知识进行结合。
我们原来做模型一般都是凭经验、直觉或基于非常强的假设做的设计,这些模型和算法普适性很好,可以在很大的空间中得到问题较好的解,但对于更具体的任务,特别是我们很多时候关心的具体问题的解是在一个较小的空间中的,普世的模型和算法就未必是最优的方法,不能充分挖掘这个小空间的结构,而深度学习方法却可以很好的刻画这些空间,这也是为什么深度学习方法在很多具体问题中都比传统方法要好。但是理论上,我们一直不知道怎么去描述这个小的空间,也就没法很好的解释为什么深度学习有如此好的性能,这也是理论上需要进一步探索的方向。在建模方面,我们需要把传统建模思想和深度学习思想融合,其关键是甄别哪些环节我们应该用传统的方法,哪些环节我们又需要利用机器学习的工具?这个目前已有很多成功的例子,但是整体规律和原则并不是很清楚,很多时候只能是Case by Case,需要有一个系统的指导。
这些年,我认为进展是大家意识到了我们需要把机理和数据融合。但我们还不是很清楚,到底是否存在一些系统的指导性原则,来指导AI更好的解决实际问题。
张平文:感谢以上六位专家分别从机器学习、统计学和应用数学三个角度来讲述数理基础的研究进展。
但什么是“人工智能的数理基础”呢?我觉得这个目前我们还说不太清楚。首先,它还不是一个成熟的领域,还不是一个被明确定义的领域。也正是因为这样,广大的青年学者就有很大的机会;因为在全球范围内人工智能数理基础研究方面的领导者还没有产生,所以大家都有机会。
第一,当前人工智能的数理基础研究最多的还是深度学习的数学理论,主要是因为第三轮人工智能的浪潮主要是因为深度学习到了,深度学习虽然在一些领域效果很好,但是人们不理解,可解释性成问题,所以这是当前最热的领域,但还有很多其它方面的研究。在我看来,应用数学,特别是计算,过去就没有可解释性的问题,因为我们都是从知识开始、从机理开始,所以没有可解释性的问题。传统的统计在我看来主要是怎么从数据到知识,就是用统计的手段,特别是在社会科学领域用得特别多,其实真正简洁与美的知识(像量子力学),并不是通过统计来的,主要是靠天才的努力。但是这样的东西毕竟有限,大量的还是社会科学、复杂科学,这里没有那么高的精度,但它也是知识,过去统计在里面起着极大的作用。我们来看机器学习想要干什么?实际上过去我们在数学圈子里面,阵地是划得很清楚的,从数据到知识是统计人的领域,从知识到决策或者到预测是计算人的领域。机器学习要一下子从数据到决策到预测,这就是机器学习想要干的,要把两个群体干的事情一把手接过去了,所以出现很多新的问题。当然这样挺好,但这些问题也不是短时间能够解决得了的。也就是说,可解释其实有两个层次:一个层次就是从算法的角度来说怎么可解释,另一个层次就是从模型和知识的角度来说可解释。这两个还是有区别。
第二,人工智能的数理基础真的是给了我们广义的应用数学,包含做应用数学、做统计、做机器学习甚至一些做工程的人,还有做脑科学、计算神经科学的人,真的是把我们团结在了一起,否则的话我就很难有机会来听统计学家的报告,很难有机会来听机器学习专家的报告,所以我觉得这是一个可能重构广义应用数学的机会,是一个非常重要的方向。
今天有非常多的年轻人在这里。所以我想强调:这个领域还不成熟,没有领导者,但它确实具有活力,所以希望大家投身到我们人工智能的数理基础这样一个研究领域,不断地在大家的努力下让它变得更加成熟,然后做出一些原创性的成果。你们有很多的机遇,但挑战也不小。
挑战:人工智能基础理论研究当前最核心的挑战还有哪些?
朱宏图:统计学整个的理论基础都是基于线性模型做起来的,但我们现在想要处理的系统和问题太复杂,旧的一套框架完全不能适应这个发展,所以这个理论已经不能满足需求。现在大家做机器学习的人,一上来就说我有一个具体的问题,然后搜集一组数据,如果能够标注的话,我就是用这个标注的数据去做后面所有模型的开发算法,跳过整个理论研究去做。对于更复杂的系统我们基本上就开始做模拟器,尽量去模拟这个物理系统里面的粒子之间的交互或者人与人之间的交互,那么从模拟器的角度去做后面所有我认为重要的模块,所以这些东西是现有的数学以及所有的理论科学目前为止不知道怎么去刻画这个系统,就会造成理论和实践是有一个很大的间隙。因为能够证明出来的都是一些比较简单的情形,但我的情形比你的更复杂,所以基本就搞不定。因此我们面临的最大的挑战就是,我们对我们的目标没有一个很深刻的数学或其它的理论框架去刻画,以前那些简单的、比较容易处理的数学工具还是无效,所以造成了我们面临的挑战非常之大。
张志华:现在最大的挑战肯定还是深度学习的挑战。原来我们大部分的统计模型都是基于浅层的,一般都是一个凸问题,我们研究这个问题就相对比较容易,比如原来我做计算数学,计算数学本身原来可能就是一个连续方程,然后怎样去解它,这些数学的问题相对比较明确。对于深度学习只有两个问题,第一,数学刻画不明确,我们用一个什么样的数学定义去证明什么东西;第二,用什么样的工具能够解决这个问题,现在也不是那么清楚。这是我认为的核心挑战。
季春霖:我想和大家探讨一下网络中不确定性的分析。现在我们在做经典的人脸识别的时候,都会把图像嵌入到空间里面,大家研究的时候更多关注的就是嵌入空间怎么设计比较合理,怎么度量嵌入比较合理,这样的话能够得到一个比较好的泛化能力。其实嵌入空间中是填不满,还有很多空余的区域。针对这些空余的区域,经典的统计方法中,偏离主要关注区域的话概率比较小,它至少有一个概率的描述,但 深度学习却没有专门描述这些区域,这里可能和安全性比较高的AI领域有非常大的关系,描述一些风险事件就需要这种刻画。现在深度学习当中没有这种不确定性的刻画,或者做的相对比较少,人们不能像经典的贝叶斯模型可以把后验概率全部取样出来,网络这么大也不可能对参数所有的样本取样。现在人们在尝试着去做,但是这方面的工作还是做得不足,没有一个完整的方法去把这个不确定性和网络结合在一起。
朱占星:其实说到机器学习,一个很重要的问题就是表示学习。从2006年Hinton发《Science》的时候就有了,DNN或者受限玻尔兹曼机,能够学到一个好的表示。到现在已经有十多年了,但也没有搞清楚什么是深度学习学到的表示。这个难点在于深度学习是由很多小的Building Block堆起来的,每个block都可能对想要关心的表示都有关系。我们之前考虑的统计都是从线性模型做起来,这些模型求解起来比较困难,但根本不用关心学习,直接分析最优化就完事。但深度学习是非凸的,这个事情就和怎么选数据、怎么学习有很大的关系,不同的学习策略就会有不同的结果。所以现在大家的数据复杂了,模型也是非凸的,学习策略也很多样化,相互之间非常依赖,我们没有办法解耦,拿出一个单个的东西去研究,说白了就是刚才张老师说的,我们没有什么好的数学刻画。我觉得这是目前最困难的问题,现在大家做的很多事情其实相当于把这三者之间做最大化的假设,然后放到已有的数学分析的区域去做,但我们真正关心的那些问题还离得很远。
展望:人工智能基础理论研究的下一个阶段有哪些潜在的新思路、新方向?
朱宏图:我一般做什么东西必须要有应用场景,这个东西又要足够复杂。
首先,我们的衣食住行现在已经有了IoT,所有东西都整合在一个平台上面之后,服务商和用户通过这个平台进行交易,我们叫做双边市场。双边市场某种程度上就是用IT所有的可能性,对老百姓的衣食住行各个方面进行改善。这里产生的问题比现在深度学习所做的三个主要方向(CV、NLP、语音)要更广。其实本质上来说很简单,就是你能不能给用户创造价值。
我认为最重要的点就是因果推断。有了一个Action之后,用户的满意度就提升了,效率就提高了,我要知道这个抓手是什么;从数据的层面,我要知道怎么搜集数据,找到原因,然后再提高用户的满意度。在这里面,深度学习只是一个工具而已。
另外增强学习会变得越来越重要。因为现在收集数据的频次越来越频繁,这些数据会带来一个机遇,就是我能够不断地调整模型策略,比如慢性病和高血压,不断收集数据,实时调整治疗方案。
再就是匹配的问题,就是针对用户如何做最好的服务。这个问题很早就有了,但是未来配准问题会变成非常基础的数学问题,相比以前更重要,就是我给用户提供什么样的服务是最优的,或者在什么样的环境下是最优的。这些问题和深度学习融合在一起。
未来机器学习人工智能基础理论当中这是需要考虑的几个方向。
董彬:我们知道 Regularization is the key,但有没有一种统一的视角,写出一类正则化去做分析?这是我自己比较好奇的一点。
史作强:刚才几位老师的总结当中都有提到可解释性是深度学习的一个非常关键的东西,张老师的总结我特别认同,那个可解释性实际上是分为不同的层次,我们可以考虑模型的可解释性,也可以考虑结果的可解释性,某种意义上这个结果的可解释性是更复杂的。最传统的物理模型,流体力学的方程,我们认为那些方程是可解释的,因为我们是从物理的规律推出来的;但由流体的现象,比如湍流,并不太好解释。因此,我觉得在未来可能更应该关注模型的可解释性;结果过于复杂,依赖不同的场景、不同的应用,可解释性都是不一样的。关于模型的可解释性,至少我个人考虑的一件事情,就是模仿物理问题当中的过程,我们先建立一些规律,比如动量守恒和能量守恒,利用这些规律我们把模型推出来。六七年前我看到过Stephen 有一些工作,就是从图像不变性把模型推出来。我们也可以尽量把模型限制在更小的范围内,减少模型中我们需要拟合的参数数目,尽量把模型的类型定下来,这也是我最近在思考的一些问题。
三、总结
张平文:首先特别感谢各位嘉宾在人工智能数理基础的进展、挑战和展望上发表自己的看法,大家说的都很有深度,对我们团队的研究也非常有指导意义,代表我们的团队感谢大家。
同时特别感谢北京智源人工智能研究院。我们这个方向还没有成型,还没有被明确定义,北京智源人工智能研究院就把我们这个方向作为第一个重大研究方向成立,其眼光真的是深远。这个平台能够使得我们不同领域的人聚在一起,我们今天有这样的机会非常重要。
北京智源人工智能研究院这四天的会议有很多的报告其实跟我们密切相关,特别是后天专门有一个机器学习的论坛。机器学习专家们会有不同的视角,他们的讨论跟我们也非常的近,所以我希望大家多去听一听他们的报告,很多思想性的报告都会对我们有启发。
我真的是认为人工智能数理基础这个方向对数学的发展会非常的重要。当年统计学的基础是概率论,现在已经成为了数学最核心的方向。早几年我在北大数院当常务副院长的时候有一个改革,就是要把大学数学最基础的教育从“三高”(分析、几何、代数)变成“四高”(加入概率论和随机分析)。现在概率论和随机分析已经渗透到了数学的方方面面,已经是最核心的数学。相信「学习理论」真的有可能在基础数学方面有新的突破,现在有人开始研究「离散拓扑」,「组合论」也焕发新的青春,能不能产生类似概率论这样新的数学是我们期待的。尽管短时间内不太可能产生的,但也还是有这种可能性。现在我们人工智能基础更多的是关注怎么去理解机器学习(特别是深度学习)的一些算法,我们也希望有一些新的算法产生;但更高层次的研究是,我们希望人工智能能够回馈数学,产生类似于概率论和随机分析这样核心的数学。这需要一个过程,因为概率论有几百年的历史,真正成熟不到一百年,成为数学的核心也是最近的一二十年的事情,这是一个漫长的过程。但对人工智能的数理基础这个方向,我是充满期待。
今天有很多来听报告的年轻人,如果是学数学的,不管你是学基础数学还是学应用数学、计算数学、统计学、信息科学或者计算机科学,人工智能的数理基础是一个非常有活力、非常有前景的方向,欢迎大家加入。
![]()
![]()
![]()
![]()
![]()