2020牛客多校联赛第五场（DEFI）

D： Drop Voicing

题目

例子

示例1
输入
6
2 4 5 1 3 6
1
2
输出
2
1

示例2
输入
8
8 4 7 3 6 2 5 1
1
2
输出
5

大意

有两种操作
operation−1operation−1 取倒数第二个移到首位
operation−2operation−2 把第一个移到末尾
要求多次operation−1operation−1连在一起时次数最小

思路

用普通写法会超限，所以我们考虑dp的方法。

代码

#include 

const int N=510;
int n,ans,a[N],dp[N];

using namespace std;

int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
      scanf("%d",a+i);
    }
	for(int c=1;c<=n;c++)
	{
		memset(dp,0,sizeof(dp));
		for(int i=1;i<=n;i++)
		{
			dp[i]=1;
			for(int j=1;j<i;j++)
			{
			    if(a[j]<a[i]) 
			    {
                    dp[i]=max(dp[i],dp[j]+1);
                }
            }	
			ans=max(ans,dp[i]);	
		}
		int tmp=a[1];
		for(int i=1;i<n;i++)
		{
           a[i]=a[i+1];
        }
		a[n]=tmp;
	}
	printf("%d\n",n-ans);
}

E： Bogo Sort

题目

例子

示例1
输入
5
1 2 3 4 5
输出
1

示例2
输入
6
2 3 4 5 6 1
输出
6

大意

给出一个固定的置换，问有多少组数组可以通过这个置换得到一个有序的序列（1 2 3 … n)。

思路

因为置换是固定的，所以只需要求出一个有序的序列（1 2 3 …n）可以通过多少次置换再次回到原来的样子即可。
然后直接求出每个数经过多少次可以回到原来的位置，求出这些次数的公倍数就可以求出总的序列经过多少次可以回到原来，但这样做会超时。
可以发现每个数经过的位置是一个循环，每个处于循环中的数都可以经过相同的次数回到原来的位置，所以只需要求出每个环中的一个数需要的次数就可以了，然后求出最小公倍数。
PS：因为涉及到大数，所以使用大数模版，而使用的大数模版中没有大数对大数的取模，因为本题取模的是10^n，所以直接取大数的后n位输出即可，不需要取模。
理解来源于以下博客：
原文链接：https://blog.csdn.net/littlegoldgold/article/details/107600691
手动模拟两个例子，我们会发现实际上能够形成排列只和环中的数目有关：

该样例的答案是6。

该样例的答案是2。

发现答案和 p 的排列有关，就是所有循环节的最小公倍数

代码

#include

using namespace std;

const int MAXN=1e5+5;
int n,len=1,w,cnt;
int a[MAXN],v[MAXN],b[MAXN],pr[MAXN],pri[MAXN],ans[MAXN]={0,1};

void mul(int x)
{
    for(int i=1;i<=len;i++) ans[i]*=x;
    for(int i=1;i<len;i++) if(ans[i]>9) ans[i+1]+=ans[i]/10,ans[i]%=10;
    while(len<n&&ans[len]>9) ans[len+1]+=ans[len]/10,ans[len++]%=10;
    ans[len+1]=0;
}//高精度乘法：高精乘低精

int main()
{
	for(int i=2;i<MAXN;i++)
		if(!pri[i])
			{
				for(int j=i*2;j<MAXN;j+=i)
					pri[j]=1;
				pr[++cnt]=i;
			}//素数筛
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",a+i);
	for(int i=1;i<=n;i++)
		if(!v[i])
		{
			v[i]=b[++w]=1;
			for(int j=a[i];j!=i;j=a[j])
				v[j]=1,b[w]++;
		}//统计环的个数
	memset(pri,0,sizeof(pri));
	for(int i=1;i<=w;i++)
		for(int j=1,t=0;j<=cnt&&b[i]>1;j++)
		{
			while(b[i]%pr[j]==0){t++;b[i]/=pr[j];}
			pri[pr[j]]=max(pri[pr[j]],t);
			t=0;
		}
	for(int i=1;i<=cnt;i++)
		while(pri[pr[i]]--)
			mul(pr[i]);
	for(int i=len;i>=1;i--)
		printf("%d",ans[i]);
}

F：DPS

题目

大意

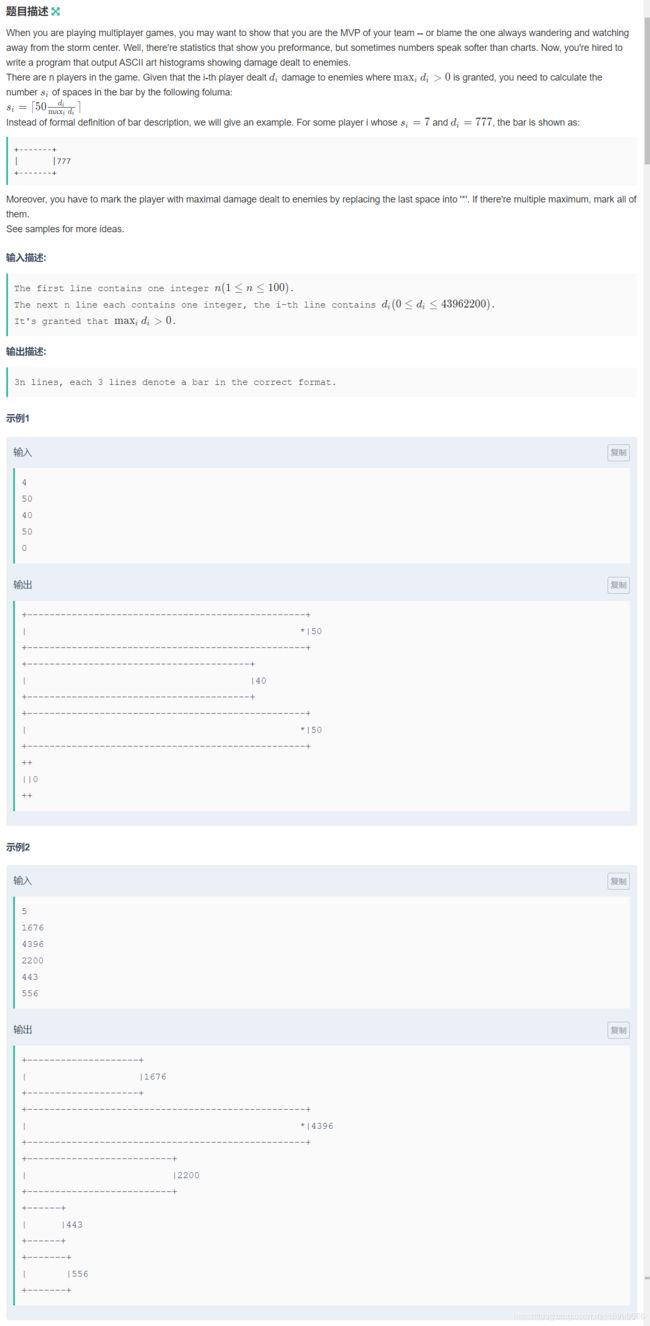
有n个玩家，每个玩家都输入他的杀伤力 di，其中：
注意 ‘-’以及 ‘空格 ’的个数为 si 的值；
‘-’：上下每行都有，数目是和空格数相等；
‘空格 ’：di*50/max（向上取整）的值；
当 di 为最大值时，需要将最后一个‘ 空格 ’ 改为 ‘ * ’ ， 如果有多个最大值，重复该操作。

思路

理解题目所给式子，打印图像即可。

代码

#include
 
using namespace std;
 
typedef long long ll;
 
int main()
{
    ll n,ant[111],max=-1,i,j;
    double q;
    cin>>n;
 
    for(i=0; i<n; i++)
    {
        cin>>ant[i];
        if(max<ant[i])
        {
            max=ant[i];
        }
    }
 
    for(i=0; i<n; i++)
    {
        cout<<'+';
        if((ant[i]*50%max)==0)
        {
            q=ant[i]*50/max;
        }
        else
        {
            q=ant[i]*50/max+1;
        }
        for(j=0; j<q; j++)
        {
            cout<<'-';
        }
        cout<<'+'<<endl;
        for(j=0; j<q+2; j++)
        {
            if(j==0||j==q+1)
            {
                cout<<'|';
            }
            else if(j==q&&ant[i]==max)
            {
                cout<<'*';
            }
            else
            {
                cout<<' ';
            }
        }
        cout<<ant[i]<<endl;
        cout<<'+';
        for(j=0; j<q; j++)
        {
            cout<<'-';
        }
        cout<<'+'<<endl;
    }
    return 0;
}

I：Hard Math Problem

题目

大意

思维题。
给出一个n*m的网格，每个格子都可放H，E或G中的一个，要求H的四周至少要有一个E和一个G。问当n、m都取 ∞ 时H的占比 (即H占总格数的多少).
如图：在斜线上交错摆E和G，而斜线上侧和下侧都可以摆放H，占比最大为2/3。

代码

#include 
#define ll long long

using namespace std;

int main()
{
    cout<<0.666667<<endl;
}