Zero-knowledge inner product argument（IPA）

接之前博客qesa——零知识证明，需要trusted setup。

---

• 注意：无论是在qesa还是bulletproofs中，inner-product的challenge x向量和y向量的选择应满足如下特征：$z_l=z_{j-i=l}=x_i{y}_j，当取l=0时，应有：z_0=x_0{y}_0=x_1{y}_1=...=x_n{y}_n$

---

2019年论文《Efficient zero-knowledge arguments in the discrete log setting,revisited (Full version)》第四章：
在protocol 3.9基础上，以$k=2$为例（$k$取2值可最小化交互信息量），$[A]w=[t]$可转化为以点积（inner product）方式表示为：
$<[A],w>=[t]$。
根据protocol 3.9第二步，prover仅需给verifier传递$[u_{\pm 1}]=<[A_i],w_j>（其中j-i=\pm 1）$。

$k=2$时，$[A]=\left(\begin{array}{c}{A}_0\\ A_1\end{array}\right)，w=\left(\begin{array}{c}{w}_0\\ w_1\end{array}\right)$，如需证明$<[A],w>=[A]w=t=A_0{w}_0+A_1{w}_1$，在第三步和第四步，引入了challeng $x=(1,\xi ),y=(\xi ,1)$，改为证明：
$t^{\prime }=<x[A],yw>=(A_0+\xi A_1)(\xi w_0+w_1)=\xi (A_0{w}_0+A_1{w}_1)+{\xi }^2{A}_1{w}_0+A_0{w}_1=\xi t+{\xi }^2<A_1,w_0>+<A_0,w_1>=\xi t+{\xi }^2{u}_{-1}+u_1$。

1. Bulletproofs的Inner-product argument

2017年论文Bulletproofs: Short Proofs for Confidential Transactions and More第三章，分别取的是$x=(\xi ,{\xi }^{-1}),y=({\xi }^{-1},\xi )$。

qesa中的Protocol 4.1（除了其中的Step 0），与Bulletproofs中的Protocol 1（论文中challenge固定为$x=(\xi ,{\xi }^{-1}),y=({\xi }^{-1},\xi )$）完全相同。具体的代码实现可参见https://github.com/crate-crypto/qesa/blob/master/src/ipa/no_zk.rs中的实现。其中challenge x向量和y向量的取值分别为：$x=(1,\xi ),y=(\xi ,1)$。

2. qesa的zero-knowledge Inner product argument (IPA)

qesa在bulletproofs IPA(inner product argument)的基础上引入了zero-knowledge。引入的方式为由原来的证明：
$<w^{\prime },w^{\prime \prime }>=t$
改为证明（借助kernel特征）：
$<\beta w^{\prime }+r^{\prime },\beta w^{\prime \prime }+r^{\prime \prime }>=t，其中<r^{\prime },w^{\prime \prime }>=<w^{\prime },r^{\prime \prime }>=<r,r^{\prime \prime }>=0$

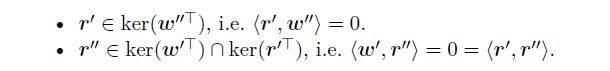
$r^{\prime }和r^{\prime \prime }$的获取方式可参考https://github.com/crate-crypto/qesa/blob/master/src/ipa/gramschmidt.rs中代码：

	//1. Compute r' and r''
    //
    let r_prime = sample_gram_schmidt(&b_Vec);

    let r_prime_prime = sample_gram_schmidt_twice(&a_Vec, &r_prime);

/// Samples a random matrix and returns a random vector
/// which is orthogonal to `a`
pub fn sample_gram_schmidt(a: &[Scalar]) -> Vec {
    let sampled_matrix = sample_m_n_plus(a.len());
    orth(a, &sampled_matrix)
}
/// Samples a random matrix and returns a random vector
/// which is orthogonal to `a` and to `b`
/// XXX: We can make a better API for this and naming convention
/// XXX: Naming it sample_gram_schmidt twice could imply that we sample twice
pub fn sample_gram_schmidt_twice(a: &[Scalar], b: &[Scalar]) -> Vec {
    let orth_a_b = orth(a, &b);
    let orth_a_sample = sample_gram_schmidt(a);

    orth(&orth_a_b, &orth_a_sample)
}
fn sample_m_n_plus(n: usize) -> Vec {
    let mut r: Vec = vec![Scalar::zero(); n];

    let mut rng = rand::thread_rng();

    r[0] = Scalar::random(&mut rng);
    r[1] = Scalar::random(&mut rng);

    let mut i = 4;
    while i <= n {
        r[i / 2] = Scalar::random(&mut rng);
        r[i / 2 + 1] = Scalar::random(&mut rng);

        i = i * 2
    }

    r[n - 2] = Scalar::random(&mut rng);
    r[n - 1] = Scalar::random(&mut rng);

    assert_eq!(n, r.len());

    r
}

/// Returns an vector that is orthogonal to `a`
/// Formally, this function projects `b` orthogonally onto the
/// line spanned by `a`
pub fn orth(a: &[Scalar], b: &[Scalar]) -> Vec {
    let aa: Scalar = inner_product(&a, &a);
    let ab: Scalar = inner_product(&a, &b);

    assert_ne!(Scalar::zero(), ab);

    let x: Scalar = ab * aa.invert();

    let ax: Vec = a.iter().map(|k| k * x).collect();

    let b_minus_ax = b.iter().zip(ax.iter()).map(|(r, s)| r - s).collect();

    b_minus_ax
}

详细的实现过程见qesa论文 protocol 4.3.

参考资料：
[1] 2019年论文《Efficient zero-knowledge arguments in the discrete log setting,revisited (Full version)》
[2] https://github.com/topics/zero-knowledge?o=desc&s=stars
[3] 博客Inner Product点积的零知识证明
[4] 2017年论文Bulletproofs: Short Proofs for Confidential Transactions and More