Python算法《字符串》

常规的正则及匹配等这里不赘述

看下比较高级的算法

一、KMP 算法

暴力匹配

暴力匹配方法的思想非常朴素：

依次从主串的首字符开始，与模式串逐一进行匹配；
遇到失配时，则移到主串的第二个字符，将其与模式串首字符比较，逐一进行匹配；
重复上述步骤，直至能匹配上，或剩下主串的长度不足以进行匹配。
参考代码如下：

def brute_force_match(t,p):
    tlen=len(t)
    plen=len(p)
    for i in range(tlen):
        j=0
        while t[i+j]==p[j] and j 

算法复杂度分析：i 在主串上移动 (n-p)次，匹配失败时，j 移动次数最多有 p-1 次。因此复杂度为 O(n*p)。

对于暴力匹配而言，就存在重复匹配的现象。比如，第一次匹配失败时，主串，模式串失败匹配的位置的字符分别为 a 与 c ,下一次匹配时主串，模式串的起始位置分别为 T[1] 与 P[0]；而在模式串中 c 之前是 ab ，未有重复结构，因此 T[1]与 P[0]肯定不能匹配上，这样造成了重复匹配。直观上，下一次匹配应从 T[2] 与 P[0] 开始。

那么如何提高匹配效率呢？那就考虑下 KMP 算法。

KMP 详细证明

KMP 算法思想归纳如下：将主串 T 的第一个字符与模式串 P 的第一个字符进行匹配。如果相等，则依次比较 T 和 P 的下一个字符。如果不相等，则 主串 T 移动(已匹配字符数-对应的部分匹配值)位，继续匹配。

关于移动位数的解释：已匹配字符数，即当前已完成匹配的字符数量。部分匹配值就是前缀和后缀的最长的共有元素的长度。

前缀指除了最后一个字符以外，一个字符串的全部头部组合。

后缀指除了第一个字符以外，一个字符串的全部尾部组合。

举个例子：以"ABCDABD"为例

"A"的前缀和后缀都为空集，共有元素的长度为 0；
"AB"的前缀为[A]，后缀为[B]，共有元素的长度为 0；
"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度 0；
"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为 0；
"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为 1；
"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为 2；
"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为 0。
部分匹配表如下：

搜索值    A    B    C    D    A    B    D
部分匹配值    0    0    0    0    1    2    0

def get_failure_array(pattern): #制作部分匹配表
    failure = [0]
    i = 0
    j = 1
    while j < len(pattern):
        if pattern[i] == pattern[j]:
            i += 1
        elif i > 0:
            i = failure[i-1]
            continue
        j += 1
        failure.append(i)
    return failure
def kmp(pattern, text):
    failure = get_failure_array(pattern) #得到部分匹配表
    i=0
    j=0
    while i < len(text):
        if pattern[j] == text[i]:
            if j == (len(pattern) - 1):
                return True
            j += 1
        elif j > 0:
            j = failure[j - 1]
            continue
        i += 1
    return False
if __name__=="__main__":
    print(kmp('123456','123123456'))

编辑距离

编辑距离(levenshtein distance)是针对二个字符串（例如英文字）的差异程度的量化量测，量测方式是看至少需要多少次的处理才能将一个字符串变成另一个字符串。编辑距离可以用在自然语言处理中，例如拼写检查可以根据一个拼错的字和其他正确的字的编辑距离，判断哪一个（或哪几个）是比较可能的字。DNA 也可以视为用 A、C、G 和 T 组成的字符串，因此编辑距离也用在生物信息学中，判断二个 DNA 的类似程度。Unix 下的 diff 及 patch 即是利用编辑距离来进行文本编辑对比的例子。

注：定义来自百度百科

算法原理
编辑距离允许的编辑操作有三种，如果字符相等，我们还可以选择不操作。我们可以列举一下这四种操作的情况。

不操作：对于"ay"与"day"的 "y"字符，可以选择不操作。即"ay"与"day"之间的利文斯顿距离等于"a"和"da"之间的利文斯顿距离。

替换操作：对于"day"与"dae"的最后一位字符"y"和"e"字符,可以选择进行替换操作。即"day"与"dae"之间的利文斯顿距离等于"da"和"da"之间的利文斯顿距离加上一。

插入操作：对于"dae"与"da"的最后一位字符"e"和"a"字符,可以选择进行插入操作。即"dae"与"da"之间的利文斯顿距离等于"da"和"da"之间的利文斯顿距离加上一。

删除操作：对于"dae"与"daey"的最后一位字符"e"和"a"字符,可以选择进行删除操作。即"dae"与"daey"之间的利文斯顿距离等于"dae"和"dae"之间的利文斯顿距离加上一。

def levenshtein_distance(first_word,second_word):
    if len(first_word)

马拉车算法

马拉车算法(Manacher)由一个叫 Manacher 的人在 1975 年发明的，这个方法的最大贡献是在于将时间复杂度提升到了线性，这是非常了不起的。让我们来看下马拉车算法的优越性在哪。

(1) 解决长度奇偶性带来的对称轴位置问题:Manacher 算法首先对字符串做一个预处理，在所有的空隙位置(包括首尾)插入同样的符号，要求这个符号是不会在原串中出现的。这样会使得所有的串都是奇数长度的。以插入#号为例：

aba->#a#b#a# abba->#a#b#b#a#

插入的是同样的符号，且符号不存在于原串，因此子串的回文性不受影响，原来是回文的串，插完之后还是回文的，原来不是回文的，依然不会是回文的。

(2) 解决重复访问的问题:我们把一个回文串中最左或最右位置的字符与其对称轴的距离称为回文半径。Manacher 定义了一个回文半径数组 RL，用 RL[i]表示以第 i 个字符为对称轴的回文串的回文半径。我们一般对字符串从左往右处理，因此这里定义 RL[i]为第 i 个字符为对称轴的回文串的最右一个字符与字符 i 的距离。对于上面插入分隔符之后的两个串，可以得到 RL 数组。

char:    # a # b # a #
RL  :    1 2 1 4 1 2 1
RL-1:    0 1 0 3 0 1 0
i   :    0 1 2 3 4 5 6

char:    # a # b # b # a #
RL  :    1 2 1 2 5 2 1 2 1
RL-1:    0 1 0 1 4 1 0 1 0
i   :    0 1 2 3 4 5 6 7 8
上面我们还求了一下 RL[i]-1。通过观察可以发现，RL[i]-1 的值，正是在原本那个没有插入过分隔符的串中，以位置 i 为对称轴的最长回文串的长度。那么只要我们求出了 RL 数组，就能得到最长回文子串的长度。

于是问题变成了，怎样高效地求的 RL 数组。基本思路是利用回文串的对称性，扩展回文串。

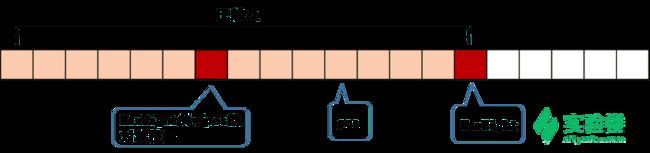
我们再引入一个辅助变量 MaxRight，表示当前访问到的所有回文子串，所能触及的最右一个字符的位置。另外还要记录下 MaxRight 对应的回文串的对称轴所在的位置，记为 pos，它们的位置关系如下。位置关系

我们从左往右地访问字符串来求 RL，假设当前访问到的位置为 i，即要求 RL[i]，在对应上图，i 必然是在 po 右边的(obviously)。但我们更关注的是，i 是在 MaxRight 的左边还是右边。我们分情况来讨论。

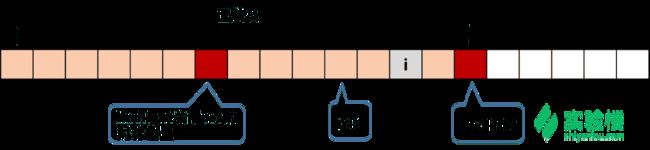
1） 当 i 在 MaxRight 的左边

位置关系

我们知道，图中两个红色块之间（包括红色块）的串是回文的；并且以 i 为对称轴的回文串，是与红色块间的回文串有所重叠的。我们找到 i 关于 pos 的对称位置 j，这个 j 对应的 RL[j]我们是已经算过的。根据回文串的对称性，以 i 为对称轴的回文串和以 j 为对称轴的回文串，有一部分是相同的。这里又有两种细分的情况。

a.以 j 为对称轴的回文串比较短

位置关系

这时我们知道 RL[i]至少不会小于 RL[j]，并且已经知道了部分的以 i 为中心的回文串，于是可以令 RL[i]=RL[j]。但是以 i 为对称轴的回文串可能实际上更长，因此我们试着以 i 为对称轴，继续往左右两边扩展，直到左右两边字符不同，或者到达边界。

b.以 j 为对称轴的回文串比较长

位置关系

这时，我们只能确定，两条蓝线之间的部分（即不超过 MaxRight 的部分）是回文的，于是从这个长度开始，尝试以 i 为中心向左右两边扩展，，直到左右两边字符不同，或者到达边界。

不论以上哪种情况，之后都要尝试更新 MaxRight 和 pos，因为有可能得到更大的 MaxRight。

具体操作如下：

令 RL[i]=min(RL[2*pos-i], MaxRight-i)
以 i 为中心扩展回文串，直到左右两边字符不同，或者到达边界
更新 MaxRight 和 pos
2) 当 i 在 MaxRight 的右边

位置关系

遇到这种情况，说明以 i 为对称轴的回文串还没有任何一个部分被访问过，于是只能从 i 的左右两边开始尝试扩展了，当左右两边字符不同，或者到达字符串边界时停止。然后更新 MaxRight 和 pos

 

def manacher(s):
    #预处理
    s='#'+'#'.join(s)+'#'

    RL=[0]*len(s)
    MaxRight=0
    pos=0
    MaxLen=0
    for i in range(len(s)):
        if i=0 and i+RL[i]MaxRight:
            MaxRight=RL[i]+i-1
            pos=i
        #更新最长回文串的长度
        MaxLen=max(MaxLen, RL[i])
    return MaxLen-1

https://www.shiyanlou.com/courses/1265/learning