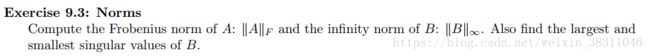高级编程技术(Python)作业13
from scipy.linalg import toeplitz
import numpy as np
def compute(A, B, lamda):
temp = B - lamda * np.eye(500)
return A @ temp
A = np.random.standard_normal((200, 500))
B = toeplitz(list(range(0, 500)))
ApA = A + A
AmAt = A @ A.T
AtmA = A.T @ A
AmB = A @ B
print("A =")
print(A)
print("\nB =")
print(B)
print("\nA + A =")
print(ApA)
print("\nAAt =")
print(AmAt)
print("\nAtA =")
print(AtmA)
print("\nAB =")
print(AmB)
print("\nA(B-Iλ) = ")
lamda = np.random.randint(1, 254)
print(compute(A, B, lamda))Output:
A =
[[ 0.63527689 -0.46965411 -0.08144386 ... 0.99068757 0.24196114
2.46171393]
[ 0.16796722 -0.60395727 1.35046286 ... 1.17290856 -0.40837032
0.89156049]
[ 2.26451677 1.39258995 1.21977885 ... 0.08485108 -1.01412036
-0.34401827]
...
[-1.44848543 -0.53995438 1.19615986 ... -0.12222356 1.70176326
-0.0234794 ]
[-0.05456266 1.17431131 0.5153051 ... 0.15164733 0.5956557
-2.02930834]
[-0.53588379 -0.30198579 -0.25434934 ... -1.04304831 0.5700688
-0.20671051]]
B =
[[ 0 1 2 ... 497 498 499]
[ 1 0 1 ... 496 497 498]
[ 2 1 0 ... 495 496 497]
...
[497 496 495 ... 0 1 2]
[498 497 496 ... 1 0 1]
[499 498 497 ... 2 1 0]]
A + A =
[[ 1.27055378 -0.93930821 -0.16288772 ... 1.98137514 0.48392227
4.92342786]
[ 0.33593445 -1.20791454 2.70092572 ... 2.34581713 -0.81674065
1.78312097]
[ 4.52903355 2.78517989 2.43955771 ... 0.16970215 -2.02824072
-0.68803653]
...
[-2.89697086 -1.07990876 2.39231972 ... -0.24444712 3.40352652
-0.04695881]
[-0.10912533 2.34862261 1.03061021 ... 0.30329466 1.1913114
-4.05861668]
[-1.07176758 -0.60397159 -0.50869867 ... -2.08609662 1.1401376
-0.41342101]]
AAt =
[[519.54293441 14.3904712 -2.9505389 ... -21.90000768 2.02306948
-3.41645362]
[ 14.3904712 440.50130118 -33.85362696 ... 22.19478433 -23.30267606
-11.96390157]
[ -2.9505389 -33.85362696 493.58048886 ... -13.15129537 2.14798488
54.67429124]
...
[-21.90000768 22.19478433 -13.15129537 ... 516.97485101 -21.01454409
-4.02739196]
[ 2.02306948 -23.30267606 2.14798488 ... -21.01454409 454.00573306
16.10363589]
[ -3.41645362 -11.96390157 54.67429124 ... -4.02739196 16.10363589
542.97716628]]
AtA =
[[184.71382733 0.6795867 16.36261 ... -26.47664379 -25.59999917
-1.96203064]
[ 0.6795867 203.74206579 4.55367036 ... -11.39796967 -23.80483802
-18.47184855]
[ 16.36261 4.55367036 203.0411682 ... 20.43336526 11.52491627
-3.95755536]
...
[-26.47664379 -11.39796967 20.43336526 ... 176.76151718 12.5619039
-13.31237111]
[-25.59999917 -23.80483802 11.52491627 ... 12.5619039 231.9201409
11.53468903]
[ -1.96203064 -18.47184855 -3.95755536 ... -13.31237111 11.53468903
262.08339928]]
AB =
[[ -7184.3574239 -7162.43392549 -7141.44973529 ... -3069.82528224
-3095.88557701 -3121.46194951]
[ -6291.33132701 -6284.02075838 -6277.91810429 ... 2827.68763872
2819.74662421 2810.98886905]
[ -3179.20304615 -3142.99021659 -3103.99220715 ... -12571.04788375
-12600.01540251 -12631.01116198]
...
[ -5702.54085177 -5676.44978707 -5651.43863112 ... -8701.20321744
-8733.54782072 -8762.48889748]
[-10470.5670167 -10440.26969865 -10407.62375799 ... -4648.36126303
-4675.90040113 -4702.24822783]
[ -3061.39377938 -3074.01560292 -3087.24139805 ... 8802.08488601
8812.90822537 8824.87170234]]
A(B-Iλ) =
[[ -7279.64895714 -7091.98580961 -7129.23315648 ... -3218.42841751
-3132.17974739 -3490.7190393 ]
[ -6316.52641052 -6193.42716775 -6480.4875335 ... 2651.751354
2881.00217284 2677.25479597]
[ -3518.88056222 -3351.87870853 -3286.95903519 ... -12583.77554526
-12447.89734833 -12579.40842218]
...
[ -5485.26803707 -5595.4566301 -5830.86260986 ... -8682.86968343
-8988.81230938 -8758.96698679]
[-10462.38261708 -10616.41639449 -10484.91952362 ... -4671.1083626
-4765.24875629 -4397.85197701]
[ -2981.0112107 -3028.71773383 -3049.08899754 ... 8958.54213287
8727.39790535 8855.87827824]]b = np.array(list(range(0, 500)))
x = np.linalg.solve(B, b)
print("\n Solve Bx = b, and get x = \n", x)Output:
Solve Bx = b, and get x =
[ 1.00000000e+00 -1.20281567e-27 5.55111512e-17 -1.11022302e-16
-2.22044605e-16 6.66133815e-16 -4.44089210e-16 -4.92308369e-27
4.44089210e-16 -1.33226763e-15 1.77635684e-15 -8.88178420e-16
...
-2.37289360e-27 2.97873878e-27 -2.32240650e-27 -1.08547261e-27
2.27191941e-27 -1.91850972e-27 1.79229198e-27 -5.42736303e-28
-1.51461294e-28 -1.88064440e-27 -2.84217094e-14 2.84217094e-14]Fro_norm_for_A = np.linalg.norm(A, 'fro')
Inf_norm_for_B = np.linalg.norm(B, np.inf)
u, s, vh = np.linalg.svd(B)
largest_value = max(s)
smallest_value = min(s)
print("\nlargest singular value is ", largest_value)
print("smallest singular value is ", smallest_value)Output:
largest singular value is 86851.66898467168
smallest singular value is 0.50000493483471import time
import numpy as np
def power_iteration(Z, n):
start = time.clock()
b_k = np.random.standard_normal(n)
old_norm = 1000
new_norm = 1000
cnt = 0
while(True):
cnt += 1
old_norm = new_norm
b_k1 = b_k @ Z
b_k1_norm = np.linalg.norm(b_k1, np.inf)
b_k = b_k1 / b_k1_norm
new_norm = b_k1_norm
if(abs(old_norm-new_norm) < 0.0001):
break
end = time.clock()
T = end - start
print("the largest eigenvalue:", b_k1_norm)
print("the corresponding eigenvector:", b_k)
print("the number of iterations:", cnt)
print("computing time for n = %d is %.3fs" % (n, T))
n = 100
Z = np.random.standard_normal((n, n))
power_iteration(Z, n)Outout:
n = 100:
the largest eigenvalue: 11.068088233359687
the corresponding eigenvector: [-0.2944245 -0.22318278 0.32930188 0.16652893 -0.18671432 0.1033079
-0.43079565 -0.06757289 -0.23260499 -0.26774119 -0.02095388 0.01306529
0.07476483 0.72441983 -0.051148 -0.05055061 -0.10833943 -0.13528726
-0.12779153 0.24640859 -0.174878 -0.63527586 0.58981573 0.64681457
-0.29897181 -0.48018419 0.05681275 1. -0.00627435 -0.36424601
0.0143298 0.10627736 -0.45038955 -0.19567988 0.21500549 -0.20055526
0.10586666 -0.19353277 0.46092431 0.06506723 0.5968188 0.15199873
0.7420006 0.46032591 -0.02483576 -0.2949899 -0.18934441 -0.80883885
-0.24025505 -0.23677737 -0.70489411 -0.12813257 -0.33248621 -0.39345534
0.40717082 -0.77745637 -0.55848406 0.16120735 -0.13881272 0.0977156
0.0308597 0.53181834 -0.02230041 0.76887701 -0.20394658 0.11921737
-0.10243752 -0.33448665 0.0029017 -0.10277001 0.01786354 0.20901145
-0.5368839 -0.72974602 -0.20956522 0.32944598 -0.08409827 -0.19542284
0.86377975 -0.34299062 -0.52208403 -0.14712398 -0.17957801 0.19866612
0.03280761 -0.30087161 -0.12790014 0.03411339 0.54760192 0.55866826
0.27828528 0.00197266 -0.11427112 0.84978421 -0.28409862 -0.3365838
0.41414519 -0.22929057 0.22212446 -0.56226912]
the number of iterations: 1338
computing time for n = 100 is 0.095sn = 1000
the largest eigenvalue: 31.451726620620093
the corresponding eigenvector: [-3.67723062e-01 2.29867064e-01 2.51742840e-01 -1.79455868e-02
5.04008912e-01 4.12574268e-01 1.95029166e-01 1.15594965e-01
3.74950571e-01 -7.71544262e-03 2.28021228e-01 -8.53313186e-02
2.22506787e-01 -7.48276906e-01 5.83083702e-02 -1.81471910e-01
...
-1.65448767e-01 -7.66347760e-01 3.25175204e-02 -3.44718183e-01
-4.24661983e-01 3.13930755e-01 2.49665989e-01 -3.24210108e-01
1.01066408e-01 -3.38146873e-01 4.17035416e-01 -2.08158123e-01]
the number of iterations: 14054
computing time for n = 1000 is 7.798s注释:事实上,当n变大的时候也时间和迭代次数不一定会变大,这个迭代次数取决于计算的矩阵特性,和一开始b_k矩阵的特性,迭代次数较大可能意味着这个矩阵不收敛,因为并不是所有的正态分布的矩阵都是收敛的。
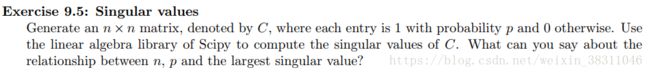
Solution:
import numpy as np
for n in [10, 20, 30]:
for p in [0.25, 0.50, 0.75]:
print("n = %d, p = %.2f" % (n,p))
C = np.random.binomial(1, p, (n, n))
u, s, vh = np.linalg.svd(C)
print("the singular values of C are: ")
for value in s:
print("%.2f" % value, end=" ")
maxvalue = max(s)
print("\nthe larset singular value is: ", maxvalue)
print("n * p: ", n*p, end="\n\n")Output:
n = 10, p = 0.25
the singular values of C are:
3.34 2.08 1.94 1.34 1.32 0.75 0.67 0.37 0.22 0.00
the larset singular value is: 3.3381035284614593
n * p: 2.5
n = 10, p = 0.50
the singular values of C are:
5.46 2.73 2.55 1.67 1.35 1.21 0.90 0.52 0.30 0.00
the larset singular value is: 5.45755368360496
n * p: 5.0
n = 10, p = 0.75
the singular values of C are:
7.60 2.43 2.01 1.54 1.09 1.00 0.72 0.42 0.15 0.00
the larset singular value is: 7.598226322714773
n * p: 7.5
n = 20, p = 0.25
the singular values of C are:
6.25 3.66 3.14 2.79 2.56 2.50 2.31 2.13 1.87 1.74 1.59 1.39 1.26 1.09 0.89 0.61 0.39 0.26 0.19 0.03
the larset singular value is: 6.2486372435890285
n * p: 5.0
n = 20, p = 0.50
the singular values of C are:
10.26 4.06 3.61 3.35 3.17 2.93 2.56 2.30 2.24 2.07 1.69 1.36 1.26 1.01 0.93 0.74 0.61 0.26 0.23 0.06
the larset singular value is: 10.259488286339908
n * p: 10.0
n = 20, p = 0.75
the singular values of C are:
15.46 3.21 3.09 3.00 2.75 2.38 2.16 1.97 1.88 1.75 1.60 1.53 1.24 1.04 0.90 0.54 0.33 0.29 0.22 0.10
the larset singular value is: 15.457854613602697
n * p: 15.0
n = 30, p = 0.25
the singular values of C are:
8.17 4.55 4.23 3.97 3.64 3.35 3.24 2.88 2.79 2.60 2.55 2.46 2.26 2.05 1.96 1.80 1.54 1.53 1.23 1.17 1.10 0.97 0.90 0.73 0.66 0.43 0.36 0.34 0.15 0.10
the larset singular value is: 8.174664215684738
n * p: 7.5
n = 30, p = 0.50
the singular values of C are:
15.33 5.17 4.77 4.62 4.12 3.91 3.89 3.54 3.21 3.13 2.91 2.88 2.63 2.48 2.33 2.25 2.11 1.81 1.69 1.56 1.37 1.26 1.02 0.93 0.78 0.69 0.56 0.32 0.22 0.11
the larset singular value is: 15.32571688028713
n * p: 15.0
n = 30, p = 0.75
the singular values of C are:
22.14 4.47 4.33 3.95 3.91 3.52 3.35 3.31 3.04 2.85 2.73 2.57 2.50 2.01 1.93 1.82 1.69 1.52 1.40 1.36 1.25 1.05 1.00 0.91 0.85 0.61 0.45 0.29 0.20 0.01
the larset singular value is: 22.13899094271687
n * p: 22.5
注释:当n 和 p逐渐增大的时候,最大的特征值也开始逐渐接近n*p

Solution:
import numpy as np
A = np.random.standard_normal((200, 500))
print("A =")
print(A)
z = input("\nPlease give a value to z: ")
z = float(z)
print("z = ", z)
print("the nearest neighbor in A is ", A.flatten()[np.argmin(np.abs(A-z))])Output:
A =
[[ 0.16978732 0.90922799 1.57803628 ... -0.94090241 -0.90116503
1.18149994]
[-0.94495112 0.49088629 0.39733231 ... -0.39165062 0.67323871
-2.73955901]
[-0.68621472 0.67000602 -2.29200515 ... 0.00739803 -0.09910325
-1.6808361 ]
...
[ 0.63333291 1.00799629 0.23079636 ... -0.24659729 -0.35720556
0.04880485]
[-0.56683618 0.25756957 -1.29729843 ... 1.14639432 -1.60384547
1.36067139]
[-1.39205996 -0.4861746 -0.21603671 ... 1.95942107 -0.98680696
-0.11168355]]
Please give a value to z: 5
z = 5.0
the nearest neighbor in A is 4.299794939351856注释:我对”use brackets and argmin”的理解是使用一行带很多括号以及使用了argmin的代码解决这个问题。A.flatten()是将这个矩阵变为一维矩阵,得到index之后方便返回所对应的值。