星系模拟器开发日志(二) 各个组件
2015.8.13更新:
上一章中解决了基本的画图技术,现在就该写真正的程序组件了。
我们将程序分成四个组件:
1)物理学组件physical module,包含基础的物理学和数学工具。
2)场景组件scene,包含场景相关的定义和方法。
3)绘图组件plotting,包含绘图方法。
4)头文件constants.h,包含程序中可能用到的诸多常量。
先写物理学组件physical module.h/cpp。
出于显然的原因,所有值均按国际单位制。
物理学组件包含:
①坐标类Vec3,成员是x,y,z三个坐标,均为float。Vec3这个名字沿用自OpenGL标准。之所以是三维是为了给将来(可能的)改成立体留余地。
②质点类Partical。成员:当前位置(Vec3),质量(float),速度(Vec3)。其中速度的方向就是向量的指向,大小则为向量的模长。
③向量加减、数乘、求模长等数学函数
④求一个质点对另一个质点所产生重力加速度的函数。公式就是a=G*m2/r^2,其中m2是施力物的质量,r是二者距离。这个公式其实就是万有引力公式约掉m1得到的。写着并不难,主要是逻辑结构要清晰。
万有引力常数G定义在constants.h中。
现在尚未解决“两点间距离为零”的问题,这个bug怎么处理我还没想好,姑且先放着
然后写场景组件scene.h/cpp。
为了未来魔改方便,写两个类:
①物体类Object,成员:将该物体视作的质点(Partical),颜色(int),颜色就是显示在屏幕上的颜色了……
②场景类Scene,成员:所有物体列表(vector
Read其实就是OI中烂大街的那种读入了……用ifstream打开一个文件,然后读入各个物体。每个物体五个数(都是float):x坐标,y坐标,质量,速度x坐标,速度y坐标。
重点说一下Step_Move。它需要传入一个参数dt,代表从现在的状态推算dt时间之后的状态。由于三体问题没有一般解析解,所以这必然只是一个近似的模拟。这里采用的思路是:对于每个物体,假设其速度为v,我们计算当前时刻它所受到的加速度dv,然后假定它的速度在这dt时间内始终保持v+dv不变。这相当于假设速度只在当前时刻瞬间变化,然后一直做了时长为dt的匀速直线运动。
这个模型是可以修改的,比如说换做假定该物体在dt时间内做匀加速运动。这一点以后看情况再说。
然后是绘图组件plotting.h/cpp。
现在,我们的绘图方式是每一帧将所有物体都画在屏幕上。因而,绘图组件包含三个函数:
①将实际坐标转换成屏幕坐标的函数Coordinate_Transform。注意,这里需要一个有“比例尺”Plotting_Scale,它定义在constants.h中。
②在屏幕上显示一个物体(Object)的函数Plot_On_Graph。方法就是先用Coordinate_Transform转换坐标,然后再用EGE的绘制填充椭圆函数进行绘制。
③在屏幕上显示一个场景(Scene)中所有物体的函数Plot_On_Graph(重载了②)。方法就是遍历储存物体的vector,一个一个绘制。
最后还有一个constants.h,里面存放诸多常量。
把所有组件写好了,呼……睡觉去了,明天试着把它们合一块跑通。
8.14更新:
首先解决了“单独开一个控制台输出”的问题:
//打开一个控制台窗口
if (AllocConsole()) {
freopen("CONOUT$", "w", stdout);
}然后该写主cpp,即Solar Simulator.cpp了。
主要思路就是:
①先读取各物体
②进行循环,每次在屏幕上绘制所有物体
③之后让整个场景演进一小段时间
写完之后跑了一个例子,发现两个质点飞快地相离而去……然后发现“演进一步”的函数写挫了,不管dt是几都相当于加速了一秒钟。果断改。然后还修了几个小bug,程序算是初步能运行了。
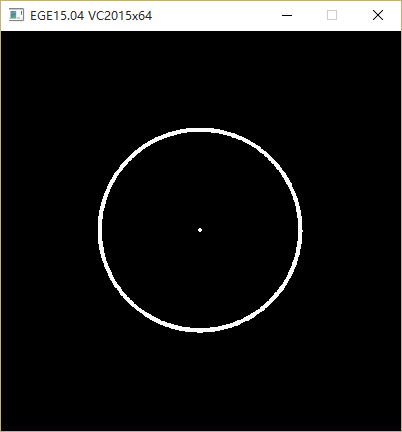
效果图:
点是一个物体,椭圆是另一个物体的轨迹。把“另一个物体”的质量设为了零,所以中央那个点并不移动。由于懒得算比例尺了,我把引力常数调成了4……
放一个三体问题的轨迹图:
这个版本是v1.0。
然后接着改。
先改一个明显的问题:v1.0中很多参数都放在了contsants.h中,这样每改一次就要重新编译一次,并不优美。所以把它改成:config.txt中,每次运行之前读取。这样就需要用fscanf。不过fscanf会报错,而我又懒得学fscanf_s了,姑且把那个报错先关掉。
这样需要修改各常数的生命方式。需要建一个constants.cpp,在这里定义所有的数值,然后在constants.h中将它们都extern一下,这样才能达到各文件共享的目的。
然后就是修改物理模型:改为假定一个物体在dt时间内做匀加速运动,即加速度不变。
这样的运行结果科学了一些,但还是存在问题:
那个螺旋形轨道本来应该是一条圆轨道的……这弄得跟蚊香似的。
原因就是:匀加速运动不可避免地让物体总是有着与其同向的加速度分量,因此速度不断加快。
怎么减小这个误差呢?容易想到的就是:缩小每一步的时间间隔。所以我们设立一个值Frame_Step_Cnt,代表每一帧都要计算这么多步。
改为每帧100步(上图较之每帧时长相同,但每帧只有一步),就好多了:
效果拔群!
再玩一个三体模型:
如果跑v1.0图中那个三体模型的话,其实结果是很不一样的:
(混沌系统的锅,怪我咯……)
测试中可以发现,当每帧步数不同时结果甚至会有很大差异,主要是在某些特定帧步数时,两物体会很快地“弹飞”而去。这可能就是那个“距离为零”的问题,也可能是别的。我猜原因之一可能是:在距离很小的时候,加速度的改变非常剧烈,这就让“加速度在dt内恒定”的预设和现实产生较大偏差。这一点应设法予以解决。但反正是混沌系统,不要在意这种细节……
8.16更新:
更换为匀加速模型,并且在config.txt中读入参数的版本是v1.1.
懒癌发作不想接着写了,歇两天……