C++递归创建、非递归遍历二叉树的基本操作
最近学了二叉树,这个数据结构和它的名字一样,真是二叉。如果单纯的让我想这样的算法,以笔者的脑子想一辈子都想不出来。二叉树刚学完,老师又讲了图。
俗话说,不能在一棵树上吊死,那我选择在二叉树上吊死。关键是图还在下面扯着你,二叉树这个数据结构不会真的是憋死人。
下面,我将我各种查阅书籍与上网翻找得出的结果告诉大家,让大家能够清楚地了解二叉树的基本操作。
#include
using namespace std;
#define MAXSIZE 100
class BTNode{
public:
char data;
BTNode *leftChild;
BTNode *rightChild;
BTNode():leftChild(NULL),rightChild(NULL){}
};
class binaryTree{
private:
BTNode *root;
public:
binaryTree();
~binaryTree();
void deleteTree (BTNode *rt);
BTNode *create_Tree();
BTNode *getRoot();
void PreOrder(BTNode *root);
void InOrder(BTNode *root);
void PostOrder(BTNode *root);
void LevelOrder(BTNode *root);
};
binaryTree::binaryTree()
{
root = create_Tree();
}
binaryTree::~binaryTree()
{
deleteTree(root);
}
BTNode *binaryTree::create_Tree()
{
BTNode *root;
char ch;
cin>>ch;
if(ch == '#')
root = NULL;
else
{
root = new BTNode;
root->data = ch;
root->leftChild = create_Tree();
root->rightChild = create_Tree();
}
return root;
}
void binaryTree::deleteTree (BTNode *rt)
{
if (rt!=NULL)
{
deleteTree(rt->leftChild);
deleteTree(rt->rightChild);
delete rt;
}
}
BTNode *binaryTree::getRoot()
{
return root;
}
void binaryTree::PreOrder(BTNode *root) //先序周游非递归算法(用栈实现)
{
BTNode *st[MAXSIZE],*p = NULL;
int top = -1;
if(root != NULL)
{
top++;
st[top] = root; //根节点入栈
while(top>-1) //判断当栈非空时循环
{
p = st[top]; //栈顶内容赋给p(即将输入的内容存放在p中)
top--;
cout<data<<" "; //输出栈顶内容
if(p->rightChild != NULL) //右孩子入栈
{
top++;
st[top] = p->rightChild;
}
if(p->leftChild != NULL) //左孩子入栈
{
top++;
st[top] = p->leftChild;
}
}
cout<-1 || p !=NULL) //当栈不为空且root存在的时候,开始遍历左孩子
{
while(p !=NULL) //将root进栈,并将指针向左孩子方向移动,直到移动至叶子
{
top++;
st[top] = p;
p = p->leftChild;
} //左孩子部分已遍历完
if(top>-1) //开始函数的输出部分
{
p = st[top]; //将左孩子放入栈中并准备输出
top--;
cout<data<<" ";
p = p->rightChild; //将指针移动到具有相同父节点的右孩子上
}
}
cout<leftChild; //指针指向左孩子,直到叶子
}
p = NULL; //将p置空,防止野指针出现
flag = 1; //设置下标
while(top != -1 && flag)
{
root = st[top];
if(root->rightChild == p) //此时的叶节点的右孩子不存在的时候
{
cout<data<<" ";//直接输出当前节点的数据
top--;
p = root; //p指向刚刚被访问的节点
}
else
{
root = root->rightChild;//
flag = 0;
}
}
}while(top != -1);
cout<data<<" ";
if(q->leftChild !=NULL)
st[rear++] = q->leftChild;//将左孩子存储至队列尾
if(q->rightChild !=NULL)
st[rear++] = q->rightChild;//将右孩子存储至队列尾
}
}
cout< 以上是整体代码,下面进行分步讲解:
BTNode *binaryTree::create_Tree()
{
BTNode *root;
char ch;
cin>>ch;
if(ch == '#')
root = NULL;
else
{
root = new BTNode;
root->data = ch;
root->leftChild = create_Tree();
root->rightChild = create_Tree();
}
return root;
}
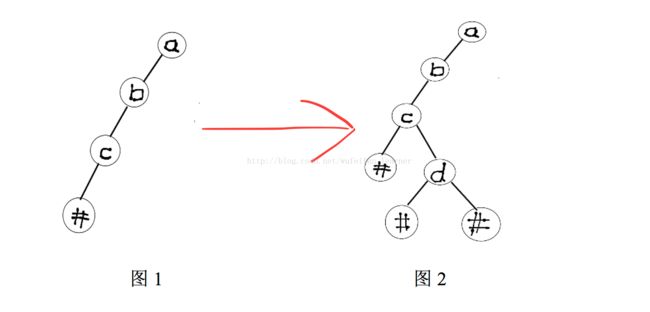
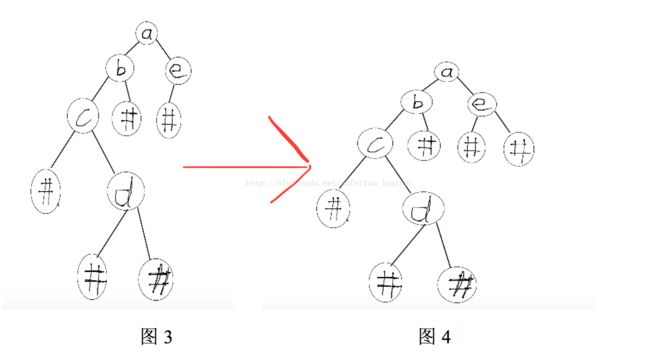
void binaryTree::PreOrder(BTNode *root) //先序周游非递归算法(用栈实现)
{
BTNode *st[MAXSIZE],*p = NULL;
int top = -1;
if(root != NULL)
{
top++;
st[top] = root; //根节点入栈
while(top>-1) //判断当栈非空时循环
{
p = st[top]; //栈顶内容赋给p(即将输入的内容存放在p中)
top--;
cout<data<<" "; //输出栈顶内容
if(p->rightChild != NULL) //右孩子入栈
{
top++;
st[top] = p->rightChild;
}
if(p->leftChild != NULL) //左孩子入栈
{
top++;
st[top] = p->leftChild;
}
}
cout<-1 || p != NULL) //当栈不为空且root存在的时候,开始遍历左孩子
{
while(p != NULL) //将root进栈,并将指针向左孩子方向移动,直到移动至叶子
{
top++;
st[top] = p;
p = p->leftChild;
} //左孩子部分已遍历完
if(top>-1) //开始函数的输出部分
{
p = st[top]; //将左孩子放入栈中并准备输出
top--;
cout<data<<" ";
p = p->rightChild; //将指针移动到具有相同父节点的右孩子上
}
}
cout< 先序周游与中序周游所用到的思想一样,借助栈来存放元素,通过栈的特性打印元素。一个元素出栈并输出,两个元素入栈,再次让一个元素出栈,再两个元素入栈,反复,直到输出所有结果。不同之处在根的处理。
void binaryTree::PostOrder(BTNode *root) //后序周游非递归实现(借用栈与下标)
{
BTNode *st[MAXSIZE],*p = NULL;
int flag,top = -1; //flag为所设下标
if(root != NULL)
{
do
{
while(root != NULL) //将左节点入栈
{
top++;
st[top] = root; //逐步实现将左孩子放进栈中
root = root->leftChild; //指针指向左孩子,直到叶子
}
p = NULL; //将p置空,防止野指针出现
flag = 1; //设置下标
while(top != -1 && flag)
{
root = st[top];
if(root->rightChild == p) //此时的叶节点的右孩子不存在的时候
{
cout<data<<" "; //直接输出当前节点的数据
top--;
p = root; //p指向刚刚被访问的节点
}
else
{
root = root->rightChild;//
flag = 0;
}
}
}while(top != -1);
cout< 后序周游难度最大,借助栈与下标实现。先将左子树的做节点入栈,指针p置空,下标置为一。如果次节点的右孩子为空,直接输出数据;如果不为空,则将指针指向右孩子,将下标置0,从根节点开始再次重复上述过程。
void binaryTree::LevelOrder(BTNode *root) //层序遍历(广度优先周游)二叉树算法实现(借助队列实现)
{
int front = 0,rear = 0; //设置下标
BTNode *st[MAXSIZE]; //队列
BTNode *q;
if(root == NULL) return; //当二叉树判空时,直接返回
else{
st[rear++] = root; //根节点存入队列
while(front != rear)
{
q = st[front++]; //由于是队列存储,控制下标,,准备输出
cout<data<<" ";
if(q->leftChild != NULL)
st[rear++] = q->leftChild; //将左孩子存储至队列尾
if(q->rightChild != NULL)
st[rear++] = q->rightChild;//将右孩子存储至队列尾
}
}
cout< 深度优先周游:
时间复杂度:每个节点访问一次,因此时间复杂度为o(n)
空间复杂度:空间主要输借助了栈,因此最差情况栈的容量等于树高,为
o(n)
广度优先周游:
时间复杂度:o(n)
空间复杂度:空间利用了队列,队列最大长度为(n+1)/2
二叉树算法是现阶段学习的重要算法,也是难点。其存储结构为链式存储结构,创建过程利用了递归思想。周游过程若用递归思想,算法的实现便会简化很多。
在今后的学习工作中,我们应该以实际情况选取递归或者非递归的方式去实现二叉树的周游。递归在系统内部调用栈的数据结构,容易溢出,而迭代则是不容易溢出,但是占用了更大的存储空间。迭代的效率要大于递归。