自然语言处理——语言模型(二)

引言

本文主要介绍N-Gram语言模型相关知识。

N-Gram

从上篇文章，我们知道。基于马尔科夫假设，假设当前词出现的概率只依赖于前$n-1$个词，我们能定义N-Gram模型如下：

$$P(w_i|w_1{w}_2\cdots w_{i-1})\approx P(w_i|w_{i-(n-1)}\cdots w_{i-1})$$

其中最简单的情况是$n=1$时的Unigram模型，和$n=2$时的Bigram模型。

$n=1$ (Unigram,假设每个单词都是独立的)：
$$P(w_1{w}_2\cdots w_n)\approx \prod _i^{n}P(w_i)$$

$n=2$ (Bigram，只依赖前面一个词)：
$$P(w_1{w}_2\cdots w_n)\approx \prod _i^{n}P(w_i|w_{i-1})$$

我们来看下Unigram是如何计算下面两句话的概率的。
$$\begin{gathered} p(今天,是,春节,我们,都,休息)=p(今天)\cdot p(是)\cdot p(春节)\cdot p(我们)\cdot p(都)\cdot p(休息) \\ p(今天,春节,是,都,我们,休息)=p(今天)\cdot p(春节)\cdot p(是)\cdot p(都)\cdot p(我们)\cdot p(休息) \end{gathered}$$

我们知道这两句话中“今天春节是都我们休息”是不通顺的，我们希望语言模型能给这句话一个很低的概率。
但在Unigram模型下，可以看出这两句话的概率是相等的。这就是Unigram模型不考虑单词顺序(单词独立)的弊端。

那Bigram模型呢，
$$\begin{gathered} p(今天,是,春节,我们,都,休息)=p(今天)\cdot p(是|今天)\cdot p(春节|是)\cdot p(我们|春节)\cdot p(都|我们)\cdot p(休息|都) \\ p(今天,春节,是,都,我们,休息)=p(今天)\cdot p(春节|今天)\cdot p(是|春节)\cdot p(都|是)\cdot p(我们|都)\cdot p(休息|我们) \end{gathered}$$

从这里可以看出来，由于Bigram模型考虑了前一个单词，这里可以很容易看出来第一句话是优于第二句话的。比如“今天是”比“今天春节”更加常见（通顺），“我们都”比“都我们”更加常见。

那Bigram只考虑了前面一个单词就能得到更好的结果，如果我们多考虑前面几个单词呢。这就是N-Gram模型。
有一点是肯定的，考虑前面单词越多，能得到的效果越好。那是不是真的越多越好呢。

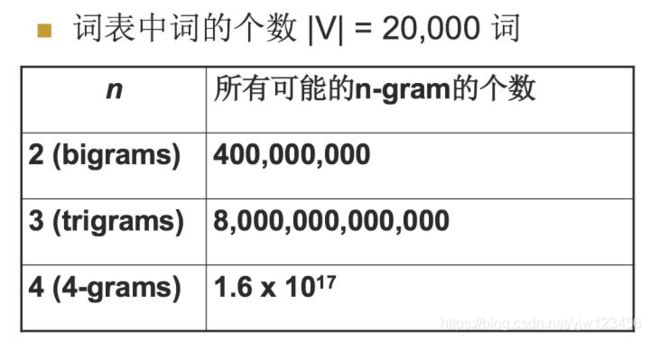
上面是假设词典中的单词个数为20000个时，所有可能的n-gram的个数。当$n=2$时，我们可以接受，甚至说$n=3$时也可以接受，但如果$n>3$的时候，这个数量我们就不能接受了。

所以考虑到时间空间的开销之后，一般$n=1,2,3$就够了。

估计语言模型的概率

在上一篇文章中，我们假设已经知道这些概率。这些概率就是语言模型的概率，本节来探讨一下如何估计语言模型的概率。

Unigram

首先来看下Unigram模型，

$$P(w_1{w}_2\cdots w_n)\approx \prod _i^{n}P(w_i)$$

在Unigram模型中，我们只要计算$p(w_i)i=1,2,\cdots ,n$的概率。即只要计算每个单词的概率，就是用语料库中每个单词出现的次数除以语料库的单词总数。

假设这是我们的语料库，其中我们出现了100次，记为$C(我们)=100$，而单词总数$V=100000$。

那么$p(我们)=\frac{100}{100000}=0.001$。

下面来看一个简单的例子，假设语料库中的单词如下：

现在想要评估“今天/开始/训练营/课程”和“今天/没有/训练营/课程”这两句话的概率。

$p(今天,开始,训练营,课程)=p(今天)\cdot p(开始)\cdot p(训练营)\cdot p(课程)$

我们分别来计算上面每个单词的概率，首先统计语料库中单词总数$V=19$，$C(今天)=2$，所以$p(今天)=\frac{2}{19}$。

同理可以计算出每个单词的概率。
$$\begin{array}{rl}p(今天,开始,训练营,课程)& =p(今天)\cdot p(开始)\cdot p(训练营)\cdot p(课程)\\ & =\frac{2}{19}\times \frac{1}{19}\times \frac{1}{19}\times \frac{1}{19}=\frac{2}{19^4}\end{array}$$

下面看第二个句子“今天/没有/训练营/课程”的概率。
$$\begin{array}{rl}p(今天,没有,训练营,课程)& =p(今天)\cdot p(没有)\cdot p(训练营)\cdot p(课程)\\ & =\frac{2}{19}\times \frac{0}{19}\times \frac{1}{19}\times \frac{1}{19}=0\end{array}$$

因为单词“没有”未出现在语料库中，导致它的概率为零，最终让整个句子的概率为零。
这个句子显然是合理的，但是其概率为零是不合理的。

为零弥补这样的缺点，我们需要采用平滑的方法，就是在分母和分子上增加一个项，使得不会出现概率为零的情况。这个我们后面会讲。

Bigram

上面是Unigram的情况，那Bigram模型要怎么估计概率呢。

$$P(w_1{w}_2\cdots w_n)\approx \prod _i^{n}P(w_i|w_{i-1})$$

假设我们要计算$p(是|明天)$，要怎么计算呢。

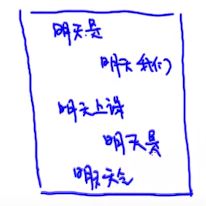
假设我们有个这样的语料库，其中“明天”出现了5次，其中有2次是“明天”后面接“是”的。

那么$P(是|明天)=\frac{2}{5}$，就是“明天”后面出现“是”的次数 除以 “明天”出现的次数。
同理可以计算出$P(我们|明天)=\frac{1}{5},P(天气|明天)=\frac{1}{5},P(上课|明天)=\frac{1}{5}$。

下面也用一个具体的例子来阐述。

我们有一个这样的语料库，要计算“今天/上午/想/出去/运动”和“今天/上午/的/天气/很好/呢”。

首先看第一句话。
$p(今天,上午,想,出去,运动)=p(今天)\cdot p(上午|今天)\cdot p(想|上午)\cdot p(出去|想)\cdot p(运动|出去)$

可以看到，虽然是Bigram模型，其中也出现了单词单词的情况$p(今天)$，这个概率就要使用类似Unigram的情况来计算。

语料库中单词总数$V=19$，“今天”出现的次数$C(今天)=2$，因此$p(今天)=\frac{2}{19}$。

下面重点来看下$p(上午|今天)$，已经知道$C(今天)=2$，“今天”后面出现“上午”的次数有1次。

所以$p(上午|今天)=\frac{1}{2}$

因此
$$\begin{array}{rl}p(今天,上午,想,出去,运动)& =p(今天)\cdot p(上午|今天)\cdot p(想|上午)\cdot p(出去|想)\cdot p(运动|出去)\\ & =\frac{2}{19}\times \frac{1}{2}\times \frac{1}{1}\times \frac{1}{2}\times \frac{1}{1}\\ & =\frac{1}{38}\end{array}$$

那“今天/上午/的/天气/很好/呢”呢
$$\begin{array}{rl}p(今天,上午,的,天气,很好,呢)& =p(今天)\cdot p(上午|今天)\cdot p(的|上午)\cdot p(天气|的)\cdot p(很好|天气)\cdot p(呢|很好)\\ & =\frac{2}{19}\times \frac{1}{2}\times 0\times \frac{1}{1}\times \frac{1}{1}\times 0\\ & =0\end{array}$$

可以看到，由于“上午”后面没有出现“的”和“很好”后面没有出现“呢”，也存在概率为零的问题。

上面介绍了$n=1,2$的情况，$n>2$也是可以用同样的方法来做。

本篇文章就到这里，下篇文章将会介绍如何评估语言模型的好坏以及如何使用平滑来避免出现概率为零的情况。

参考

1. 贪心学院课程