codeforces362（div2）ABC

A. Pineapple Incident

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Ted has a pineapple. This pineapple is able to bark like a bulldog! At time t (in seconds) it barks for the first time. Then every sseconds after it, it barks twice with 1 second interval. Thus it barks at times t, t + s, t + s + 1, t + 2s, t + 2s + 1, etc.

Barney woke up in the morning and wants to eat the pineapple, but he can't eat it when it's barking. Barney plans to eat it at time x (in seconds), so he asked you to tell him if it's gonna bark at that time.

Input

The first and only line of input contains three integers t, s and x (0 ≤ t, x ≤ 109, 2 ≤ s ≤ 109) — the time the pineapple barks for the first time, the pineapple barking interval, and the time Barney wants to eat the pineapple respectively.

Output

Print a single "YES" (without quotes) if the pineapple will bark at time x or a single "NO" (without quotes) otherwise in the only line of output.

Examples

input

3 10 4

output

NO

input

3 10 3

output

YES

input

3 8 51

output

YES

input

3 8 52

output

YES

Note

In the first and the second sample cases pineapple will bark at moments 3, 13, 14, ..., so it won't bark at the moment 4 and will bark at the moment 3.

In the third and fourth sample cases pineapple will bark at moments 3, 11, 12, 19, 20, 27, 28, 35, 36, 43, 44, 51, 52, 59, ..., so it will bark at both moments 51 and 52.

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int maxn=10010;
int num[maxn];
int main()
{
    int t,s,x;
    scanf("%d%d%d",&t,&s,&x);
    if(x==t)printf("YES\n");
    else if(x-t

B. Barnicle

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Barney is standing in a bar and starring at a pretty girl. He wants to shoot her with his heart arrow but he needs to know the distance between him and the girl to make his shot accurate.

Barney asked the bar tender Carl about this distance value, but Carl was so busy talking to the customers so he wrote the distance value (it's a real number) on a napkin. The problem is that he wrote it in scientific notation. The scientific notation of some real numberx is the notation of form AeB, where A is a real number and B is an integer and x = A × 10B is true. In our case A is between 0 and 9and B is non-negative.

Barney doesn't know anything about scientific notation (as well as anything scientific at all). So he asked you to tell him the distance value in usual decimal representation with minimal number of digits after the decimal point (and no decimal point if it is an integer). See the output format for better understanding.

Input

The first and only line of input contains a single string of form a.deb where a, d and b are integers and e is usual character 'e' (0 ≤ a ≤ 9, 0 ≤ d < 10100, 0 ≤ b ≤ 100) — the scientific notation of the desired distance value.

a and b contain no leading zeros and d contains no trailing zeros (but may be equal to 0). Also, b can not be non-zero if a is zero.

Output

Print the only real number x (the desired distance value) in the only line in its decimal notation.

Thus if x is an integer, print it's integer value without decimal part and decimal point and without leading zeroes.

Otherwise print x in a form of p.q such that p is an integer that have no leading zeroes (but may be equal to zero), and q is an integer that have no trailing zeroes (and may not be equal to zero).

Examples

input

8.549e2

output

854.9

input

8.549e3

output

8549

input

0.33e0

output

0.33

题意：将科学计数法化为十进制数。

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int maxn=10010;
int num[maxn];
char a[maxn];
char b[maxn];
char str[maxn];
char ans[maxn];
int main()
{
    int num=0,dot;
    bool sign=false;
    scanf("%s",str);
    for(int i=0;str[i];++i){
        if(str[i]=='e'){
            sign=true;a[i]=0;continue;
        }
        if(sign)
            num=num*10+(str[i]-'0');
        else
            a[i]=str[i];
        if(str[i]=='.')dot=i;
    }sign=false;
    bool flag=false;
    int len=strlen(a);
    int dot1=dot+num,ans_len=0;
    for(int i=0;i='1'&&a[i]<='9')sign=true;
        if(i>=len)ans[ans_len++]='0';
        else if(a[i]!='.'){
            ans[ans_len++]=a[i];
        }
        if(i==dot1&&i=0;--i){
            if(ans[i]=='0'||ans[i]=='.')ans_len--;
            else break;
        }
    }
    if(!sign){
        printf("0\n");
        return 0;
    }sign=false;
    for(int i=0;i

C. Lorenzo Von Matterhorn

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Barney lives in NYC. NYC has infinite number of intersections numbered with positive integers starting from 1. There exists a bidirectional road between intersections i and 2i and another road between i and 2i + 1 for every positive integer i. You can clearly see that there exists a unique shortest path between any two intersections.

Initially anyone can pass any road for free. But since SlapsGiving is ahead of us, there will q consecutive events happen soon. There are two types of events:

1. Government makes a new rule. A rule can be denoted by integers v, u and w. As the result of this action, the passing fee of all roads on the shortest path from u to v increases by w dollars.

2. Barney starts moving from some intersection v and goes to intersection u where there's a girl he wants to cuddle (using his fake name Lorenzo Von Matterhorn). He always uses the shortest path (visiting minimum number of intersections or roads) between two intersections.

Government needs your calculations. For each time Barney goes to cuddle a girl, you need to tell the government how much money he should pay (sum of passing fee of all roads he passes).

Input

The first line of input contains a single integer q (1 ≤ q ≤ 1 000).

The next q lines contain the information about the events in chronological order. Each event is described in form 1 v u w if it's an event when government makes a new rule about increasing the passing fee of all roads on the shortest path from u to v by w dollars, or in form 2 v u if it's an event when Barnie goes to cuddle from the intersection v to the intersection u.

1 ≤ v, u ≤ 1018, v ≠ u, 1 ≤ w ≤ 109 states for every description line.

Output

For each event of second type print the sum of passing fee of all roads Barney passes in this event, in one line. Print the answers in chronological order of corresponding events.

Example

input

7
1 3 4 30
1 4 1 2
1 3 6 8
2 4 3
1 6 1 40
2 3 7
2 2 4

output

94
0
32

Note

In the example testcase:

Here are the intersections used:

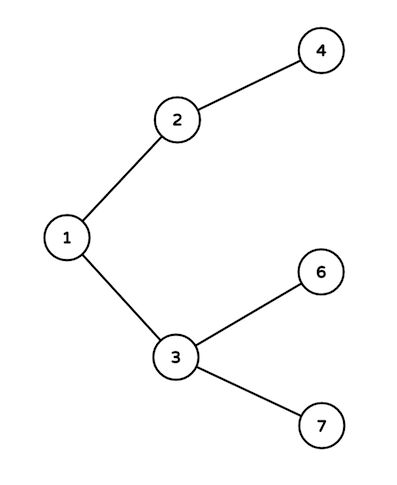
1. Intersections on the path are 3, 1, 2 and 4.
2. Intersections on the path are 4, 2 and 1.
3. Intersections on the path are only 3 and 6.
4. Intersections on the path are 4, 2, 1 and 3. Passing fee of roads on the path are 32, 32 and 30 in order. So answer equals to32 + 32 + 30 = 94.
5. Intersections on the path are 6, 3 and 1.
6. Intersections on the path are 3 and 7. Passing fee of the road between them is 0.
7. Intersections on the path are 2 and 4. Passing fee of the road between them is 32 (increased by 30 in the first event and by 2 in the second).

题意：给出一个二叉树，每次给出一条路径将这条路径上的节点加上一个数另一个操作询问一条路径上的值的累加和。

#include
#include
#include
#include
#include
#include
#include
#include
#include