A*算法的原理和实现

一：A*的介绍

A*算法是一种启发式搜索算法，就是在状态空间中的搜索对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这样可以省略大量无畏的搜索路径，提到了效率。在启发式搜索中，对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。

该算法可以用公式f(n)=g(n)+h(n)表示,其中 f(n) 是从初始点经由节点n到目标点的估价函数，g(n) 是在状态空间中从初始节点到n节点的实际代价，h(n) 是从n到目标节点最佳路径的估计代价。h*(n)是从n到目标节点最佳路径的实际代价,那么整个个启发式搜索过程必须保证h(n)<=h*(n)，否则搜索出错。

对于h(n) 的选择，越接近h*（n）则速度越快。

主要有以下几种启发函数

曼哈顿距离：

定义曼哈顿距离的正式意义为L1-距离或城市区块距离，也就是在欧几里德空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上，坐标（x1,y1）的点P1与坐标（x2, y2）的点P2的曼哈顿距离为：|x1 - x2| + |y1 - y2|。

欧氏距离：

是一个通常采用的距离定义，它是在m维空间中两个点之间的真实距离。在二维和三维空间中的欧氏距离的就是两点之间的距离。例如在平面上，坐标（x1,y1）的点P1与坐标（x2, y2）的点P2的欧氏距离为： sqrt((x1-x2)^2+(y1-y2)^2 )。

切比雪夫距离：

是两个向量之间各分量差值的最大值。例如在平面上，坐标（x1, y1）的点P1与坐标（x2, y2）的点P2的切比雪夫距离为：max(|x1 - x2| , |y1 - y2|)。

二：A*算法的过程

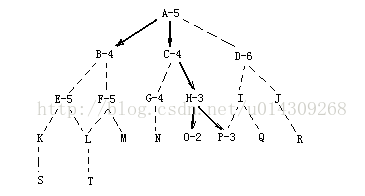
目标：要从A走到P，节点后的是估值

搜索过程中设置两个表：OPEN和CLOSED。OPEN表保存了所有已生成而未考察的节点，CLOSED表中记录已访问过的节点。算法中有一步是根据估价函数重排OPEN表。这样循环中的每一步只考虑OPEN表中状态最好的节点。具体搜索过程如下：

1）初始状态：　　　　　　　　　　　　　　　　
　OPEN=[A5]；CLOSED=[]；
2）估算A5，取得搜有子节点，并放入OPEN表中；
　OPEN=[B4，C4，D6]；CLOSED=[A5]
3）估算B4，取得搜有子节点，并放入OPEN表中；
　OPEN=[C4，E5，F5，D6]；CLOSED=[B4，A5]
4）估算C4；取得搜有子节点，并放入OPEN表中；
　OPEN=[H3，G4，E5，F5，D6]；CLOSED=[C4，B4，A5]
5）估算H3，取得搜有子节点，并放入OPEN表中；
　OPEN=[O2，P3，G4，E5，F5，D6]；CLOSED=[H3，C4，B4，A5]
6）估算O2，取得搜有子节点，并放入OPEN表中；
　OPEN=[P3，G4，E5，F5，D6]；CLOSED=[O2，H3，C4，B4，A5]
7）估算P3，已得到解；

其中，OPEN表可以用优先队列实现

代码：

POJ2243

在棋盘上，骑士走“日”的形态，求从棋盘一点到另外一点的最短步数？

#include  
#include  
#include  
#include  
using namespace std;  
int a[8][2]={{-2,-1},{-2,1},{-1,-2},{-1,2},{1,-2},{1,2},{2,-1},{2,1}},vist[9][9];  
struct node  
{  
    int x,y,step;  
    int f,g,h;  
    bool operator < (const node &anOther) const {  
        return f > anOther.f;  
    }  
};  
node s,e;  
  
int find_h(node tmp){  
  double a;
		a=((e.x-tmp.x)^2+(e.y-tmp.y)^2);
		int b=sqrt(a);
		return b*10;
}  
priority_queueque;  
  
int AStar(node start,node end)  
{  
    int i;  
    node cur,next;  
    while( !que.empty() ) que.pop();  
    que.push(start);  
    while( !que.empty() )  
    {  
        cur = que.top();  
        que.pop();  
        for(i=0;i<8;i++)  
        {  
            next.x = cur.x + a[i][0];  
            next.y = cur.y + a[i][1];  
            if( !vist[next.x][next.y] && next.x>=1 && next.x<=8 && next.y>=1 && next.y<=8 )  
            {  
                vist[ next.x ][ next.y ] = 1;  
                next.step = cur.step + 1;  
                next.g = cur.g +23;  
                next.h = find_h(next);  
                next.f = next.g + next.h;  
  
                if(next.x == end.x && next.y == end.y )  
                    return next.step;  
                que.push(next);  
            }  
        }  
    }  
    return 0;  
}  
  
int main()  
{  
    int move;  
    char t,m;  
    while( scanf("%c%d %c%d",&t,&s.y,&m,&e.y) !=EOF)  
    {  
        getchar();  
        memset(vist,0,sizeof(vist));  
        move = 0;  
        s.x = t - 'a' + 1;  
        e.x = m - 'a' + 1;  
        s.step = 0;  
        s.g = 0;  
        s.f = s.g + find_h(s);  
        vist[s.x][s.y]=1;  
        move = AStar(s,e);  
        printf("To get from %c%d to %c%d takes %d knight moves.\n",t,s.y,m,e.y,move);  
    }  
    return 0;  
}