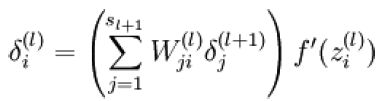DeepLearnToolbox代码详解——SAE,DAE模型
一:引言.sae,dae,dropout模型简介
上面提到的三个模型都是在经典的多层神经网络的基础上加深构架得到;例如sae(Stack autoencoder)就是理堆叠多个autoencoder,然后使用fine_tuning过程;dae(Denoising autoencoder)是在标准的sae基础上给输入数据加入噪声,利用污染后的数据进行sae;dropout 则是随机忽略隐层节点来训练多个不同的模型,然后通过模型平均来预测。
下面就详细讲解一下这个sae框架的训练过程,以及调用函数的说明。
二:实例讲解
1. 试验准备:
DeepLearnToolbox-master代码:https://github.com/rasmusbergpalm/DeepLearnToolbox
2. 文件配置:
2.1 首先打开新建的test_sae.m文件;
2.2 然后把current folder,窗口转到……matlabdlToolBox\DeepLearnToolbox-master
2.3 在command 窗口输入:addpath(genpath('.'));
2.4 打开test_sae.m,运行就ok了
2.5 等着出结果
3.网络结构说明本文以minist手写数字识别为例,输入数据为784,即visible层为784个节点。
假设我们训练的网络结构为:784——200—— 100—— 10,也就是说有4层,一个输入层,2个中间隐层;1个输出隐层,来进行预测分类。
网络结构如图:

4.主函数代码:test_sae.m
clear all; close all; clc;
%% //导入数据
load mnist_uint8;
train_x = double(train_x)/255;
test_x = double(test_x)/255;
train_y = double(train_y);
test_y = double(test_y);
%%一:采用autoencoder进行预训练
rng(0);%高版本的matlab可以使用这个语句,低版本会出错
sae = saesetup([784 200 100]);
sae.ae{1}.activation_function = 'sigm';
sae.ae{1}.learningRate = 1;
sae.ae{1}.inputZeroMaskedFraction = 0.;
sae.ae{2}.activation_function = 'sigm';
sae.ae{2}.learningRate = 1;
sae.ae{2}.inputZeroMaskedFraction = 0.;
opts.numepochs = 1;
opts.batchsize = 100;
visualize(sae.ae{1}.W{1}(:,2:end)')
%二:fine_tuning过程
% Use the SDAE to initialize a FFNN
nn = nnsetup([784 200 100 10]);
nn.activation_function = 'sigm';
nn.learningRate = 1;
%add pretrained weights
nn.W{1} = sae.ae{1}.W{1};
nn.W{2} = sae.ae{2}.W{1};
% Train the FFNN
opts.numepochs = 1;
opts.batchsize = 100;
nn = nntrain(nn, train_x, train_y, opts);
[er, bad] = nntest(nn, test_x, test_y);
str = sprintf('testing error rate is: %f',er);
disp(str)三:pre_training阶段代码详解
3.1:网络结构建立
Sae网络就是堆叠多个autoencoder网络,所以此网络结构由2个autoencoder构成,分别是:v—h1—v和h1—h2—h1.
此处主要利用saesetup函数来实现,
3.1.1 Saesetup函数说明
输入参数:size为构建网络的节点向量,由于此处pre_training阶段的网络为784-200-100;所以size=[784 200 100]
输出参数:sae元包矩阵,每一个元包矩阵对应一个autoencoder网络;例如sae.ae{1}中“存放”的就是v——h1——v这个autoencoder;
函数体说明:通过for循环2次,调用nnsetup函数两次,生成两个autoencoder
function sae =saesetup(size)
for u = 2 :numel(size)
sae.ae{u-1}= nnsetup([size(u-1) size(u) size(u-1)]);
end
end
autoencoder构建:我们知道autoencoder就是一个v——h——v 的3层神经网络;所以主要通过nnsetup来构建。
3.1.2 nnsetup函数说明
输入参数:nnsetup(architecture),architecture,顾名思义,就是构建网络的结构,也就是每层网络的神经元节点个数,例如本题为第一个autoencoder结构为v—h1—v [784 200 784]
输出参数nn:一个元包矩阵,元包矩阵中存放着一个autoencoder网络的各种配置参数
函数体说明:Encoder过程:y=f(xw'+b)
激活函数nn.activation_function:f(),一般有sigmoid和tanh两种;
学习率 nn.learningRate:控制学习的速度,
动量项 nn.momentum:调节在应用minibatch方法训练网络时,每次新权值更新值和上一次权值更行值的相对比例;
权值惩罚项 nn.weightPenaltyL2:防止权值过大,发生过拟合现象;
稀疏目标 nn.sparsityTarget:通过控制隐层激活值的平均值,来控制隐层激活值的稀疏性
Decoder过程:x=g(wy+b)
解码激活函数设置:sigmoid和tanh两种
其他参数:例如dae中的加噪比例参数,dropout中的隐层节点的忽略比例等权值W初始化:
W结构初始化:权值矩阵W的行列数,例如若使用:h=f(x*w'+b),本例中第一个autoencoder中,权值矩阵w1为200*785 ,(785=784+1,1为偏置项b,后面介绍)
W元素初始化:W的元素初始值为一个0均值的随机矩阵,权值系数很小,这样可以防止过拟合
nn.W{i - 1} = (a*b);
a=rand(nn.size(i), nn.size(i - 1)+1) - 0.5)%生产一个0均值,范围元素值在[-0.5 0.5]范围内的矩阵
b=2 * 4 * sqrt(6 / (nn.size(i) + nn.size(i - 1))%缩减矩阵元素值到一个更小的范围
3.2:网络训练阶段
此阶段主要调用saetrain函数来训练网络;
3.2.1 Seatrain函数说明
输入参数:saetrain(sae, x, opts)
Sae为step1阶段设置好的网络结构;x为输入数据;opts中有两个参数;其中opts.numepochs为训练次数,所有样本一共训练多少次;opts.batchsize参数,为在对所有样本进行minibatch训练时,每个batch的容量,即每个batch的样本个数。
输出参数:训练好的元包矩阵sae
函数体说明:通过for循环,调用nntrain函数,依次训练每个autoencoder。3.2.2 Nntrain函数说明:
输入参数:nntrain(nn, train_x, train_y, opts, val_x, val_y)
其中nn为一个元包矩阵,nn中存放的是网络的配置参数;train_x,train_y就是输入数据,和目标数据;在autoencoder网络中,都是输入数据x,opts参数,已经说过;至于val_x和val_y做什么的不清楚,训练中暂时用不到。
输出参数:[nn, L],已经训练好的网络参数,主要训练W和b,L为损失函数值,在autoencoder中是重构误差。
函数体说明:
1.minibatch部分
所谓的minibatch训练方法就是把所有训练样本分成多个batch,然后依次训练每个batch中的样本。
将训练集事先分成包含几十或几百个样本的小批量数据进行计算将更高效,这主要是可以利用图形处理器Gpu和matlab中矩阵之间相乘运算的优势。
m = size(train_x, 1);%提取样本总数
batchsize = opts.batchsize; %每个batch中样本个数
numepochs = opts.numepochs; %所有样本训练次数
numbatches = m / batchsize; %所有样本分成多少个batch
2.训练过程
for i = 1 : numepochs%所有样本训练次数
kk =randperm(m); %形成样本编号的随机向量
for l = 1 : numbatches%每次提取batchsize个样本,一共提取numbatches次
batch_x =train_x(kk((l - 1) * batchsize + 1 : l * batchsize), :);
batch_y =train_y(kk((l - 1) * batchsize + 1 : l * batchsize), :);
nn =nnff(nn, batch_x, batch_y); %前馈计算网络
nn =nnbp(nn);%计算误差和权值梯度
nn =nnapplygrads(nn);%参数更新
L(n) =nn.L;
n = n + 1;
end
end
在nntrain末尾还可以缩减学习率,使更新步长逐渐变小。
nn.learningRate = nn.learningRate *nn.scaling_learningRate;
3.2.3 前馈函数nnff说明
输入参数:nnff(nn, batch_x, batch_y),这个就不说了,和上面一样
输出参数:元包矩阵nn,主要计算了隐层的激活函数值。
函数体说明:
1 添加偏置项
x = [ones(m,1) x];
nn.a{1} = x;
一般前馈计算过程为,h=f(xw’+b);其中参数b即为偏置项;此时在计算过程中,需要“复制”b维数,是的复制后的b可以和wx乘积结果可以相加(详见 SparseAutoEncoder 稀疏编码详解));这样每次复制b,会增大计算量;本代码中,把偏置项,直接添加到输入数据x中,在x前添加一列0元素,作为偏置项b;这是样输入数据矩阵,就变成了60000*785,这也就和前面为什么要把权值矩阵w1定义为为200*785,而不是200*784了。所以最后权值矩阵W1为200*785;W2为100*201 ;W3为10*101。
这样前馈计算过程,由h=f(xw’+b),变成了h=f(x*w’)
2 encoder和decoder过程
Encoder阶段:
for i = 2 : n-1
switchnn.activation_function
case 'sigm'
% Calculate the unit's outputs (including the bias term)
nn.a{i} = sigm(nn.a{i - 1} * nn.W{i - 1}');
case 'tanh_opt'
nn.a{i} = tanh_opt(nn.a{i - 1} * nn.W{i - 1}');
end
nn.a{i} =[ones(m,1) nn.a{i}];%给下一个网络的输入添加偏置项
end
decoder阶段:
根据选择的decoder函数,来计算;由于此处是autoencoder,通过 nn.a{n} = sigm(nn.a{n - 1} * nn.W{n - 1}');来生成输入数据的近似估计,以便用来求重构误差。
switch nn.output
case 'sigm'
nn.a{n}= sigm(nn.a{n - 1} * nn.W{n - 1}');
case 'linear'
nn.a{n}= nn.a{n - 1} * nn.W{n - 1}';
case 'softmax'
nn.a{n}= nn.a{n - 1} * nn.W{n - 1}';
nn.a{n}= exp(bsxfun(@minus, nn.a{n}, max(nn.a{n},[],2)));
nn.a{n}= bsxfun(@rdivide, nn.a{n}, sum(nn.a{n}, 2));
end
3.计算损失函数
nn.e = y -nn.a{n};
switch nn.output
case {'sigm', 'linear'}
nn.L =1/2 * sum(sum(nn.e .^ 2)) / m; %均方误差
case 'softmax'
nn.L =-sum(sum(y .* log(nn.a{n}))) / m;
end
3.2.4反向函数nnbp说明:
输入,输出参数:nn = nnbp(nn),都是元胞矩阵nn
这里首先要复习一下,bp算法的误差传播方法。
误差反向传播:
最后一层误差:nl为最后一层的层数,z为最后一层的输入,上一层的输出值

Sigmoid函数的导数为f’(a)=a(1-a)
输出层误差代码:
switch nn.output
case 'sigm'
d{n} =- nn.e .* (nn.a{n} .* (1 - nn.a{n}));
case {'softmax','linear'}
d{n} =- nn.e;
end
中间层误差:本层和下一层的连接权值,乘以,上一层误差,在乘以,本层输入的导数。
for i = (n - 1) : -1 :2
% 各层激活函数求导
switchnn.activation_function
case 'sigm'
d_act = nn.a{i} .* (1 - nn.a{i});
case 'tanh_opt'
d_act = 1.7159 * 2/3 * (1 - 1/(1.7159)^2 * nn.a{i}.^2);
end
% 计算误差
if i+1==n
d{i} =(d{i + 1} * nn.W{i} + sparsityError) .* d_act;
%倒数第二层的残杀d{nl-1},是由最后一层残差d{nl}传播得到的,而最后一层的残差没有添加偏置项,也就是输出层节点是10,而不是11;所以误差可以直接通过连接的权值矩阵向前传递。
else
d{i} =(d{i + 1}(:,2:end) * nn.W{i} + sparsityError) .* d_act;
倒数第二层以前的残差d{i}是由上一层残差d{i+1}传递过来的;而中间层再向前传递的时候每层都加了偏置项,而这里我们要计算的是连接权值矩阵W的残差,所以 应该把添加的偏置项去掉,所以去挑d{i+1}的第一列,使用d{i + 1}(:,2:end),而不是整个d{i+1}。
end
end权值更新量计算:
l层的权值更新量delta_W=下一层网络的误差 * 本层输入
l层偏置项更新量delta_b=残差
为了避免在小批量数据的样本容量发生改变时,学习率也必须做相应的修改;通常的做法是在参数的更新过程中昬使用参数的平均梯度;即总梯度除以数据容量。
for i = 1 : (n - 1)
if i+1==n
nn.dW{i} = (d{i + 1}' * nn.a{i}) / size(d{i + 1}, 1);
else
nn.dW{i} = (d{i + 1}(:,2:end)' * nn.a{i}) / size(d{i + 1}, 1);
end
end权值更新:
基本的梯度下降更新:无动量项,无权值惩罚项
w=w-alpha*delta_W
for i = 1 : (nn.n - 1)
if(nn.weightPenaltyL2>0)
dW =nn.dW{i} + nn.weightPenaltyL2 * [zeros(size(nn.W{i},1),1) nn.W{i}(:,2:end)];
else
dW =nn.dW{i};
end
dW =nn.learningRate * dW;
if(nn.momentum>0)
nn.vW{i} = nn.momentum*nn.vW{i} + dW;
dW =nn.vW{i};
end
nn.W{i} =nn.W{i} - dW;
end四、fine_tuning阶段
4.1初始化网络结构
1.首先通过nnsetup(784,200,100,10)函数来构建网络;此时不是通过saesetup函数来构建;
2.设置网络激活函数,学习率等参数
3.把Pre_training阶段,学习到的权值矩阵,作为网络权值的初始值;
nn.W{1} = sae.ae{1}.W{1};
nn.W{2}= sae.ae{2}.W{1};
4.2 fine_tuning
利用nntrain函数,使用真实的标签数据train_y来微调整个网络
nn= nntrain(nn, train_x, train_y, opts);
4.3:预测阶段 (此部分代码详解见博文:Denosing Autoencoder训练过程代码详解)
[er,bad] = nntest(nn, test_x, test_y);
后记:本来想写DBN模型的代码详解来着,没想到在翻看资料的时候已经有人写好了,所以在这里就把连接贴出来了。
【面向代码】学习 Deep Learning(二)Deep Belief Nets(DBNs)