学习笔记第十一节：计算几何之平面凸包

正题

     【模板】二维凸包

      我们用这一题来进行问题的引入。

      现在要求覆盖平面上n个点的最小凸多边形。

      我们要学凸包。

      学习凸包的同时要知道几个概念。

第一个:向量（矢量）

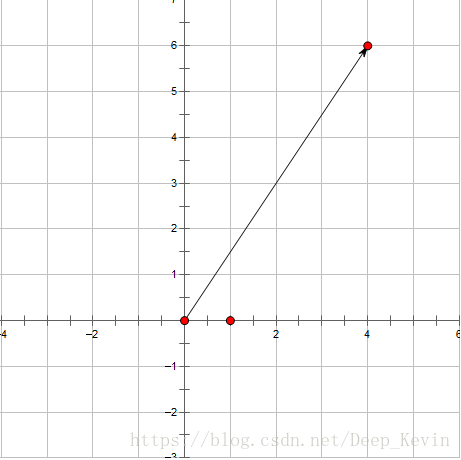
      向量(x,y)描述的是一个有方向的量。表示的相当于是从(0,0)到(x,y)的量。

      就比如说矢量(4,6)

      就是这个样子的。

      当然也有这种表示，表示这是一条从A到B的向量。

第二个：矢量积（叉积）

      两个矢量a和b的矢量积是一个矢量，记作a×b，其模（长度）等于a和b作成的平行四边形的面积，方向与平行四边形所在平面垂直，a转过一个小于π的角到达b的方向。用右手，以外腕转向内腕的方向从a转向b，那么拇指向上，则叉积>0，如果拇指向下，则叉积<0，若共线，叉积为0.

这才是

正题

      讲完上面的两个基础概念之后，我们可以开始讲凸包了。

      首先，在这里只讲Graham算法。

      它的算法流程是这样的：

      1.先找出一个y坐标最小的前提下x坐标最小的，它必然是凸包的一个顶点。

      2.连接这个点与其他点，按逆时针方向给其他点排序，那么排序的过程就是相当于一个比较叉积的过程。

node getvec(node x,node y){
	node op;
	op.x=x.x-y.x;//对于两个点，把它转化为从原点出发的一条向量
	op.y=x.y-y.y;
	return op;
}

double getcro(node t1,node t2){
	return t1.x*t2.y-t2.x*t1.y;//算叉积
}

bool cmp(node x,node y){
	double cro=getcro(getvec(s[1],x),getvec(s[1],y));//算出叉积
	return cro>0;//如果叉积大于0，说明x在y的顺时针方向，则x的排序后的编号比y小
}

      3.排好序之后，他们依次连接在一起一定不会有相交的地方，所以，凸包的顺序一定在这个顺序里面。

      4.我们先把排完序的第一个和第二个放入答案中，其他的，算出前面两个的向量与最后一个点和当前点的向量的叉积。如果叉积<0，那么说明它是一个凹角，不在凸包的答案里面。把倒数第一个答案踢出答案。

      完成操作。

#include
#include
#include
#include
#include
#include
#include
using namespace std;

int n;
struct node{
    double x,y;
}s[10010];
vector f;

node getvec(node x,node y){
	node op;
	op.x=x.x-y.x;
	op.y=x.y-y.y;
	return op;
}

double getdis(node x,node y){
	return sqrt((x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y));
}

double getcro(node t1,node t2){
	return t1.x*t2.y-t2.x*t1.y;
}

bool cmp(node x,node y){
	double cro=getcro(getvec(s[1],x),getvec(s[1],y));
	return cro>0 || (cro==0 && getdis(s[1],x)<=getdis(s[1],y));
}

bool judge(int t1,int t2,int t3){
	double cro=getcro(getvec(s[t3],s[t1]),getvec(s[t1],s[t2]));
	return cro>0 || (cro==0 && getdis(s[t3],s[t2])>=getdis(s[t3],s[t1]));
}

int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++) scanf("%lf %lf",&s[i].x,&s[i].y);
    int first=1;
    for(int i=2;i<=n;i++) if(s[i].y1 && !judge(f.back(),i,f[f.size()-2])) f.pop_back();
		f.push_back(i);
	}
	f.pop_back();
	double tot=0;
	for(int i=0;i<=f.size()-2;i++)
		tot+=getdis(s[f[i]],s[f[i+1]]);
	tot+=getdis(s[f[f.size()-1]],s[f[0]]);
	printf("%.2lf\n",tot);
	return 0;
}

例题1：Beauty Contest

      给你一张图，要你求图上最远点对距离的平方。

      凸包解决，因为凸包上的点对是最远的。

      考虑几个重要因素：1.cmp的顺序不能丢。2.考虑组不成凸包的情况（链）。

      这道题的数据很好。。。

代码相对于之前的改了

 

#include
#include
#include
#include
#include
#include
#include
using namespace std;

int n;
struct node{
	int x,y;
}s[50010];
vector f;

node getvec(node x,node y){
	node op;
	op.x=x.x-y.x;
	op.y=x.y-y.y;
	return op;
}

int getdis(node x,node y){
	return (x.x-y.x)*(x.x-y.x)+(x.y-y.y)*(x.y-y.y);
}

int getcro(node t1,node t2){
	return t1.x*t2.y-t1.y*t2.x;
}

bool cmp(node a,node b){
	int cro=getcro(getvec(s[1],a),getvec(s[1],b));
	return cro>0 || (cro==0 && getdis(s[1],a)<=getdis(s[1],b));
}

bool judge(int a,int b,int c){
	int cro=getcro(getvec(s[a],s[b]),getvec(s[b],s[c]));
	return cro>0 || (cro==0 && getdis(s[a],s[c])>=getdis(s[a],s[b]));
}

int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d %d",&s[i].x,&s[i].y);
	int first=1;
	for(int i=2;i<=n;i++) if(s[i].y1 && !judge(f[f.size()-2],f.back(),i)) f.pop_back();
		f.push_back(i);
	}
	f.pop_back();
	if(f.size()==1){
		int mmax=0;
		for(int i=1;i<=n;i++)
			for(int j=i+1;j<=n;j++)
				mmax=max(mmax,getdis(s[i],s[j]));
		printf("%d\n",mmax);
		return 0;
	}
	int mmax=0;
	for(int i=0;i