CS224D 课程学习笔记 L02

Lecture 2 主要介绍了传统的共现矩阵生成词向量方法和迭代生成词向量的方法，例如word2vec和Glove。

Word Vectors

人类对“词义”定义为通过一个词或者短语表示的意思，人想要通过词表达的意思，写作、艺术表达的意思。

计算机定义“词义”，通常是使用WordNet之类的分类方法，比如说，具有is-a关系、代名词集合。例如，“panda” is-a “animal”，“panda” is-a “vertebrate”，“good”的代名词集合有“full”，“expert”等。

首先，介绍一个可以说是最简单的词向量：

one-hot vector

one-hot向量就是将每个词表达为一个大小为|V|*1的向量，其中词所在的位置为1，其他位置全为0。|V|表示词典的大小。

这种表示方法存在的问题有：

1. 丢失了词词之间的细小的差别
2. 无法处理新词
3. 带有主观性
4. 需要人力实现
5. 很难精确计算词之间的相似性

现在，一个很成功的统计NLP想法就是，通过邻域词（上下文）来表达词的信息。

怎样通过上下文表达词呢？答案是，共现矩阵。

共现矩阵

生成共现矩阵有两种方法：整篇文档和滑动窗口。

• 整篇文档

  根据文档生成大小为|V|*M的共现矩阵，第 i 行第 j 列表示词 i 在文档 j 中出现的次数。这种方法会由主题引申到“潜语义分析”。很明显，随着文档数量M的增加，矩阵大小也在增加。

• 滑动窗口

  使用滑动窗口能够同时捕获到句法（POS）和语义信息。

  生成的共现矩阵是对称的，对角线上元素为0，矩阵大小为n*n，n表示词的个数。

共现矩阵存在的问题

在Google级别的公司处理NLP任务，词的个数会达到百万级别，这就导致了共现矩阵具有很高的维度，需要更大的存储空间。而在后续的分类等任务中，也会存在着矩阵稀疏的问题，导致模型的鲁棒性很差。

解决方法：使用低纬度的向量来存储词的大部分信息，也叫“密集向量”，通常大小为25~1000。怎样降低共现矩阵的维度呢？

接下来介绍两种方法：SVD-Based和 Iteration-Based。

SVD

对共现矩阵X应用SVD（Singular Value Decomposition）奇异值分解。奇异值分解适用于任意大小的矩阵。对于大小为n*m的矩阵X，奇异值分解为：

$X=US{V}^T$

其中，U的大小n*n，每列向量是正交的，成为左奇异向量；S的大小n*m，对角线上为奇异值，按照从大到小排列，除对角线外其他元素都是0；V的大小为m*m，列向量也是正交的，成为右奇异向量。奇异值表征的是特征向量的重要性。

复习一下SVD的求解过程：

1. $(X^{T}X)v_i={\lambda }_i{v}_i$
2. ${\sigma }_i=\sqrt{{\lambda }_i}$
3. $u_i=\frac{1}{{\sigma }_i}X{v}_i$

通常，前10%~1%的奇异值的和就占了全部的奇异值之和的99%以上，所以，经常用部分奇异值分类来近似矩阵X。得到的分解公式：

​

$X_{n\ast m}=U_{n\ast r}{S}_{r\ast r}{V}_{r\ast m}^T$

python可以通过调用numpy实现SVD：

import numpy as np
la = np.linalg
words = [“I”,”like”,”enjoy”,”deep”,”learning”,”NLP”,”flying”,”.”]
X = np.array([0,2,1,0,0,0,0,0],
                       [2,0,0,1,0,1,0,0],
                       [1,0,0,0,0,0,1,0],
                       [0,1,0,0,1,0,0,0],
                       [0,0,0,1,0,0,0,1],
                       [0,1,0,0,0,0,0,1],
                       [0,0,1,0,0,0,0,1],
                       [0,0,0,0,1,1,1,0])
U, s, vh = la.svd(X, full_matrices=False)

对于出现频率很高的词，例如“the”“she”“has”等，对X有很大的影响，所以经常采用几种补救方法：

1. 设置词频阈值，高于阈值用阈值取代
2. 忽略这些无意义的高频词
3. 滑动窗口使用斜坡窗口，即越靠近中心词，计数越多，远离中心词的词计数减少
4. 使用皮尔逊系数代替计数统计，将小于0的皮尔逊系数设置为0。

SVD存在的问题

• 计算复杂度高，当n*m大小的共现矩阵，耗费$O(m{n}^2)$的复杂度
• 对新词或者新文档难处理

SVD缺点的解决办法存在很多，与本课程和深度学习相关的主要有以下：

• Learning representations by back-propagating errors.(Rumelhart et al., 1986)
• A neural probabilistic language model (Bengio et al ., 2003)
• NLP from scratch (Collobert & Weston, 2008)
• A recent and even simpler model: word2vec (Mikolov et al., 2013)

word2vec

word2vec就是接下来我们要介绍的重点。

word2vec的主要思想是：对每个词，预测周围可能出现的词，而不是计算共现矩阵。这样，对于新词、新出现的句子和文档，也可以快速及时处理。

对于大小为c的窗口，预测目标词的上下文可能出现的词，目标函数为：

$$J(\theta )=\frac{1}{T}\sum _{t=1}^T\sum _{-c\le j\le c,j̸=0}logp(w_{t+j}|w_t)$$

即，最大化给定中心词的任意上下文词的概率。对于$p(w_{t+j}|w_t)$最简单的公式为：

​$$p(w_O|w_I)=\frac{exp(u_O^T{v}_I)}{{\sum }_{w=1}^{W}exp(u_w^T{v}_I)}$$

就是softmax函数形式，其中 $u$ 和 $v$ 分别表示词的输入向量和输出向量（每个词都有两个向量，这点很重要！）

想要优化目标函数，我们需要对公式求导求梯度，在推导的过程中，有两个知识点需要掌握：

1. 矩阵求导 $\frac{\partial X^{T}a}{\partial X}=\frac{\partial a^{T}X}{\partial X}=a$
2. 链式法则 $\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}$

对概率p进行求导：

$$\frac{\partial p(o|c)}{\partial v_c}=\frac{\partial }{\partial v_c}log(\frac{exp(u_o^T{v}_c)}{{\sum }_{w=1}^{W}exp(u_w^T{v}_c)})$$

​$$=\frac{\partial }{\partial v_c}(log(exp(u_o^T{v}_c))-log(\sum _{w=1}^{W}exp(u_w^T{v}_c)))$$

​$$=u_o-\frac{1}{{\sum }_{w=1}^{W}exp(u_w^T{v}_c)}\frac{\partial }{\partial v_c}\sum _{x=1}^{W}exp(u_x^T{v}_c)$$

​$$=u_o-\frac{1}{{\sum }_{w=1}^{W}exp(u_w^T{v}_c)}\sum _{x=1}^W\frac{\partial }{\partial v_c}exp(u_x^T{v}_c)$$

​$$=u_o-\frac{1}{{\sum }_{w=1}^{W}exp(u_w^T{v}_c)}\sum _{x=1}^{W}exp(u_x^T{v}_c)u_x$$

$$=u_o-\sum _{x=1}^W\frac{exp(u_x^T{v}_c)}{{\sum }_{w=1}^{W}exp(u_w^T{v}_c)}{u}_x$$

$$=u_o-\sum _{x=1}^{W}p(x|c)u_x$$

在第三步，使用x代替w，防止与前面求和的w混淆；在第六步对求和做简化。

具体梯度求导在Lecture 3中还会做详细介绍。

从公式中可以看出，需要所有的词做求和，当词典数量很大的时候，目标函数不可扩展，训练速度很慢。解决这个问题有两种方法，一是对归一化做近似，二是仅采样少量负样本。在作业一种，我们会推导实现负采样。

word2vec的神奇之处

word2vec学习得到的词向量非常擅长于相似性计算。主要表现在类比和语义两个方面。例如：

• 语法空间上的类比性。

  ​ $$X_{apple}-X_{apples}\approx X_{car}-X_{cars}$$

• 形态学语义上的相似性。

  ​ $$X_{king}-X_{man}=X_{queen}-X_{woman}$$

Glove

Glove这里只是简单提了一下，它的目标函数是：

​$$J=\frac{1}{2}\sum _{ij}f(P_{ij})(w_i\cdot \widetilde{w_j}-log{P}_{ij}{)}^2$$

几种得到词向量方法的对比

• 共现次数

  代表方法有LSA、HAL、COALS、Hellinger-PCA。训练速度快，有效的利用了统计学，主要用于获取词之间的相似性，不利于低频词。

• 直接推导

  代表方法有NNLM、HLBL、RNN、Skip-gram/CBOW。对于不同大小的数据集可扩展，没有利用统计学，在其他任务上表现有较好，能够获取词的复杂模式，例如类比关系。

• Glove

  训练速度快，对大文档集可扩展，对小文档或者低维向量表现也不错。

词向量是我们接下来学习的每节课的基础，所有的语义表达和NLP任务都会基于词向量来完成。深度学习得到的词向量的最大的好处就是可以在神经网络中传播他们本身带有的信息，具体内容下节课将会介绍。

Iteration Based Method

我们尝试建立一个能够迭代学习的模型，根据中心词的上下文来预测中心词出现的概率。这个概率模型有已知的参数和未知的参数，我们每次使用一个训练样本，根据输入信息、输出信息和期望得到的输出信息，来学习未知的参数。

一元、二元语言模型

例如存在这样一个句子：“The cat jumped over the puddle. ”，从语法和语义上说，这个句子是个不错的句子，它的概率应该是一个较高的值。用数学公式来表达，一个n个词组成的句子的概率为：

$$P(w^{(1)},w^{(2)},\dots ,w^{(n)})=\prod _{i=1}^{n}P(w^{(i)})$$

这就是一元模型（Unigram model）。一元模型依赖的假设条件是词与词之间是相互独立的。但是在现实中，这种假设基本不成立。所以就有了二元模型（bigram model）：

​$$P(w^{(1)},w^{(2)},\dots ,w^{(n)})=\prod _{i=2}^{n}P(w^{(i)}|w^{(i-1)})$$

虽然二元模型还是没有利用整个句子的信息，但是比一元模型进步很多。

接下来介绍两种能过学习到句子概率的模型。

CBOW

还是以上节中的句子为例，假设中心词为“jumped”，窗口C取2，那么上下文为{“The”，“cat”，“over”，“the”}，CBOW就是根据上下文预测中心词。

首先，定义已知参数：

• $x^{(i)}$ : 上下文词的one-hot vectors

• $ y^{(i)} $: 中心词的one-hot Vector

• $w^{(i)}$ : 词典V中的词i

定义未知参数：

• $W^{(1)}$ :大小为n * |V|，输入词向量矩阵
• $u^{(i)}$: $W^{(1)}$ 的第i列向量，也是词$w^{(i)}$的输入向量表达。
• $W^{(2)}$:大小为|V|*n，输出词向量矩阵
• $v^{(i)}$: $W^{(2)}$的第i航向量，也是词$w^{(i)}$的输出向量表达。

注意：每个词都有两个向量，输入向量u和输出向量v。

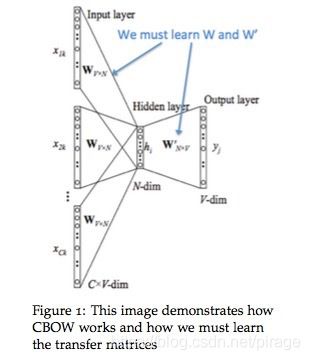
我们将CBOW模型分解为以下步骤：

1. 对窗口大小C的上下文，生成one-hot矩阵 $(x^{(i-C)},\dots ,x^{(i-1)},x^{(i+1)},\dots ,x^{(i+C)})$
2. one-hot向量左乘输入矩阵$W^{(1)}$，即可得到上下文的词向量$(u^{(i-C)}=W^{(1)}{x}^{(i-C)},u^{(i-C+1)}=W^{(1)}{x}^{(i-C+1)},\dots ,u^{(i+C)}=W^{(1)}{x}^{(i+C)}$
3. 对上下文的词向量求平均 $h=\frac{u^{(i-C)}+\dots u^{(i+C)}}{2C}$
4. 根据输出矩阵$W^{(2)}$生成得分向量 $z=W^{(2)}h$
5. 将得分转化为概率，$\hat{y}=softmax(z)$

现在我们知道了CBOW模型是如何工作的，那么怎样学习到参数$W^{(1)}$ 和 $W^{(2)}$ 呢？

首先，我们需要创建目标函数。从真实概率分布中学习未知概率分布，我们通常会根据信息论从中选择两个分布的距离度量函数，这里，我们选择交叉熵作为目标函数：

​$$H(\hat{y},y)=-\sum _{j=1}^{|V|}{y}_{i}log(\widehat{y_j})$$

因为y是one-hot向量，所以上面式子可以简化为：

$$H(\hat{y},y)=-y_{i}log(\widehat{y_j})$$

因为$y_i$是1，所以优化目标为：

​ $$minimizeJ=-logP(w^{(i)}|w^{(i-C)},\dots ,w^{(i-1)},w^{(i+1)},\dots ,w^{(i+C)})$$

​$$=-logP(v^{(i)}|h)$$

​$$=-log\frac{exp(v^{(i)T}h)}{{\sum }_{j=1}^{|V|}exp(v^{(i)T}{u}^{(j)})}$$

$$=-v^{(i)T}h+log\sum _{j=1}^{|V|}exp(v^{(i)T}{u}^{(j)})$$

接下来的问题就是，如何用梯度下降优化目标函数？

这里解释一下为什么可以用交叉熵作为目标函数？如果预测准确，$\hat{y}=1$ ,我们可以计算损失也就是交叉熵$H(\hat{y},y)=-1log(1)=0$, 如果预测不准确，假设 $\hat{y}=0.01$ ,交叉熵$H(\hat{y},y)=-1log(0.01)\approx 4.605$. 所以，对于概率分布的距离，交叉熵有很好的表现。

Skip-gram

与CBOW不同的是，Skip-gram模型是根据中心词预测上下文的词出现的概率。参数的定义同上，我们将Skip-gram模型的步骤分解为：

1. 生成中心词的one-hot向量 $x$
2. 得到上下文的词向量 $u^{(i)}=W^{(1)x}$
3. h设置为 $h=u^{(i)}=W^{(1)}x$
4. 根据 $v=W^{(2)}h$生成2C个分数向量， $v^{(i-C),\dots ,v^{i-1},v^{i+1},\dots ,v(i+C)}$
5. 将每个词的得分转化为概率， $y=softmax(v)$

同样的，我们将生成的概率与真是的上下文的词作比较，希望得到匹配的结果。

与CBOW的目标函数不同，Skip-gram使用了贝叶斯假设来推导概率，假设条件独立。换句话说，给定中心词，它的上下文词之间的关系是独立的。我们可以得到优化函数：

​ $$minimizeJ=-logP(w^{(i-C)},\dots ,w^{(i-1)},w^{(i+1)},\dots ,w^{(i+c)}|w^{(i)})$$

$$=-log\prod _{j=0,j̸=C}^{2C}P(w^{(i-C+j)}|w^{(i)})$$

​$$=-log\prod _{j=0,j̸=C}^{2C}P(v^{(i-c+j)}|u^{(i)})$$

​$$=-log\prod _{j=0,j̸=C}^{2C}\frac{exp(v^{(i-C+j)T}{u}^{(i)})}{{\sum }_{k=1}^{|V|}exp(v^{(k)T}{u}^{(i)})}$$

​$$=\sum _{j=0,j̸=C}^{2C}{v}^{(i-C+j)T}{u}^{(i)}+2Clog\sum _{k=1}^{|V|}exp(v^{(k)T}{u}^{(i)})$$

同样，在每次迭代中，我们通过计算梯度更新未知参数。

Negative Sample

回顾上述两种模型的目标函数可以发现，在迭代更新的过程中，需要计算整个词汇集|V|的和，而词的个数通常在百万级别，这就要花费大量的运算时间。一个简单的做法是可以对全部词汇做近似。

在每个训练步骤中，只采样几个负样本来代替遍历整个词汇集。我们从按照词频排序的分布$P_n(w)$中采样，把上述的公式和负采样结合在一起，我们只需要更新这些：

• 目标函数
• 梯度
• 更新法则

NS方法是Mikolov et al.在论文Distribution Representations of Words and Phrases and Their Compositionality 中提出的。NS事实上优化的是不同于上面的目标函数。存在一个中心词和上下文词对$(w,c)$，我们用$P(D=1|w,c)$表示该词对来自训练集，$P(D=0|w,c)$表示词对不存在训练数据中，首先，我们用sigmoid函数对概率P建模：

$$P(D=1|w,c,\theta )=\frac{1}{1+exp(-v_c^T{v}_w)}$$

然后，我们建立一个目标函数，来最大化出现在训练集的词对的概率和没有出现在训练集的词对的概率。我们采用简单的最大似然来计算，这里$\theta$ 就是模型的未知参数，也就是上面的模型中的$W^{(1)}$ 和 $W^{(2)}$ ，

​ $$\theta =argma{x}_{\theta }\prod _{(w,c)\in D}P(D=1|w,c,\theta )\prod _{(w,c\notin D)}P(D=0|w,c,\theta )$$

​ $$=argma{x}_{\theta }\prod _{(w,c)\in D}P(D=1|w,c,\theta )\prod _{(w,c)\notin D}(1-P(D=1|w,c,\theta ))$$

​ $$log\theta =argma{x}_{\theta }\sum _{(w,c)\in D}logP(D=1|w,c,\theta )+\sum _{(w,c)\notin D}log(1-P(D=1|w,c,\theta ))$$

​ $$=argma{x}_{\theta }\sum _{(w,c)\in D}log\frac{1}{1+exp(-v_c^T{v}_w)}+\sum _{(w,c)\notin D}log(1-\frac{1}{1+exp(-v_c^T{v}_w)})$$

​ $$=argma{x}_{\theta }\sum _{(w,c)\in D}log\frac{1}{1+exp(-v_c^T{v}_w)}+\sum _{(w,c)\notin D}log\frac{1}{1+exp(v_c^T{v}_w)}$$

其中，$(w,c)\notin D$表示负采样的样本。那么，我们的目标函数就变成了：

​ $$-log\sigma (v^{(i-C+j)}\cdot h)+\sum _{k=1}^{K}log\sigma ({\breve{v}}^{(k)}\cdot h)$$

${\breve{v}}^{(k)}|k=1\dots K$表示从分布$P_n(w)$采样的$K$个负样本。

关于什么样的分布$P_n(w)$能够使得近似效果最好的讨论有很多，看起来最好的方法是一元模型值取3/4次方，3/4能够使得低频词的采样几率被提高。