2019CCPC女生赛(重现赛)
| Solved | Pro.ID | Title | Ratio(Accepted / Submitted) |
| |
1001 | Ticket | 55.32%(369/667) |
| |
1002 | Gcd | 33.21%(268/807) |
| 1003 | Function | 22.49%(38/169) | |
| |
1004 | Tree | 34.62%(63/182) |
| 1005 | Checkout | 44.12%(15/34) | |
| 1006 | String | 41.82%(23/55) | |
| |
1007 | Circle | 32.24%(265/822) |
| 1008 | Clock | 20.30%(81/399) | |
| 1009 | Union | 35.00%(7/20) | |
| |
1010 | Tangram | 30.27%(221/730) |
| |
1011 | Tetris | 25.33%(193/762) |
1001 Ticket
Ticket
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 0 Accepted Submission(s): 0
Problem Description
北京地铁票每月的打折规则为:本次乘车前总消费不足 100 元本次不打折,满 100 元不足 150 元本次打8 折,满 150 元不足 400 元本次打 5 折,已满 400 元后本次不打折,已知 wls 每次出行的原票价,请问实际的花费是多少?
Input
输入包含两行。第一行一个整数 n 代表 wls 将要出行的次数。第二行 n 个正整数, ai 代表每次出行的票的原价,wls 是按照输入顺序依次出行的。
0 ≤ n ≤ 1, 000
0 < ai ≤ 1, 000
Output
一行一个数,代表实际的花费,保留小数点后两位小数。
Sample Input
3 100 20 20
Sample Output
132.00
Source
755hdu女生赛
签到题目,读懂题意就简单
本次乘车前总消费不足 100 元本次不打折
#include
using namespace std;
typedef long long ll;
const int N=500005;
const int MOD=1e9+7;
double a[N],b[N];
int main()
{
int n;
while(scanf("%d",&n)!=-1)
{
double ans=0;
for(int i=1;i<=n;i++)
scanf("%lf",&a[i]);
for(int i=1;i<=n;i++)
{
double temp=1;
if(ans<150&&ans>=100) temp=0.8;
else if(ans>=150&&ans<400) temp=0.5;
ans=ans+a[i]*temp;
}
printf("%.2lf\n",ans);
}
return 0;
}
1002 Gcd
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 0 Accepted Submission(s): 0
Problem Description
wls 有一个整数 n,他想将 1 − n 这 n 个数字分成两组,每一组至少有一个数,并且使得两组数字的和的最大公约数最大,请输出最大的最大公约数。
Input
输入一行一个整数 n。
2 ≤ n ≤ 1, 000, 000, 000
Output
输出一行一个整数表示答案。
Sample Input
6
Sample Output
7
Source
755hdu女生赛
分析:假设a为最后答案,sum1整除a+sum2整除a=sum整除a,倒着枚举sum的因子。
但这样超时。然后我们可以从前往后枚举i,sum%i==0,则sum/i就为答案
#include
using namespace std;
typedef long long ll;
const int N=500005;
const int MOD=1e9+7;
ll ans=0;
int main()
{
int n;
while(scanf("%lld",&n)!=-1)
{
ll sum=(n)*(n+1)/2;
for(ll i=2; i<=sum; i++)
if(sum%i==0)
{
printf("%lld\n",sum/i);
break;
}
ans=0;
}
return 0;
} 1004 Tree
Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 0 Accepted Submission(s): 0
Problem Description
wls 有三棵树,树上每个节点都有一个值 ai,现在有 2 种操作:
1. 将一条链上的所有节点的值开根号向下取整;
2. 求一条链上值的和;
链的定义是两点之间的最短路。
Input
第一行两个数 n, q 分别代表树上点的数量和操作数量。
第二行 n 个整数,第 i 个数代表第 i 个点的值 ai。
接下来 n − 1 行, 每行两个整数 u, v 代表 u,v 之间有一条边。数据保证点两两联通。
接下来 q 行,每行有个整数 op, u, v,op = 0 表示将 u, v 这条链上所有的点的值开根号向下取整,op = 1表示询问 u,v 这条链上的值的和。
1 ≤ n, q ≤ 100, 000
0 ≤ ai ≤ 1, 000, 000, 000
Output
对于每一组 op = 2 的询问,输出一行一个值表示答案。
Sample Input
4 4 2 3 4 5 1 2 2 3 2 4 0 3 4 0 1 3 1 2 3 1 1 4
Sample Output
2 4
Source
755hdu女生赛
分析:树链剖分+这道题的应用:https://blog.csdn.net/sdz20172133/article/details/87278847
第一次做树链剖分就做出来,✌
#include
#define int long long
using namespace std;
const int maxn=1e5+10;
struct edge{
int next,to;
}e[maxn*2];
struct node{
int l,r,ls,rs,sum,lazy;
int flag;
}a[maxn*2];
int n,m,r,rt,v[maxn],head[maxn],cnt,f[maxn],d[maxn],son[maxn],size[maxn],top[maxn],id[maxn],rk[maxn];
void add(int x,int y)
{
e[++cnt].next=head[x];
e[cnt].to=y;
head[x]=cnt;
}
void dfs1(int x)
{
size[x]=1,d[x]=d[f[x]]+1;
for(int v,i=head[x];i;i=e[i].next)
if((v=e[i].to)!=f[x])
{
f[v]=x,dfs1(v),size[x]+=size[v];
if(size[son[x]]>1;
a[x].ls=cnt++,a[x].rs=cnt++;
build(l,mid,a[x].ls),build(mid+1,r,a[x].rs);
a[x].l=a[a[x].ls].l,a[x].r=a[a[x].rs].r;
pushup(x);
}
inline int len(int x)
{
return a[x].r-a[x].l+1;
}
inline void pushdown(int x)
{
if(a[x].lazy)
{
int ls=a[x].ls,rs=a[x].rs,lz=a[x].lazy;
(a[ls].lazy+=lz),(a[rs].lazy+=lz);
(a[ls].sum+=lz*len(ls)),(a[rs].sum+=lz*len(rs));
a[x].lazy=0;
}
}
void update(int l,int r,int x)
{
if(a[x].l>=l&&a[x].r<=r)
{
if(a[x].flag==1)
return;
}
if(a[x].l==a[x].r)
{
a[x].sum=sqrt(a[x].sum);
if(a[x].sum==1) a[x].flag=1;
return ;
}
int mid=a[x].l+a[x].r>>1;
if(mid>=l)
update(l,r,a[x].ls);
if(mid=l&&a[x].r<=r)
return a[x].sum;
pushdown(x);
int mid=a[x].l+a[x].r>>1,tot=0;
if(mid>=l)
tot+=query(l,r,a[x].ls);
if(midid[y])
swap(x,y);
return (ret+query(id[x],id[y],rt));
}
inline void updates(int x,int y)
{
while(top[x]!=top[y])
{
if(d[top[x]]id[y])
swap(x,y);
update(id[x],id[y],rt);
}
signed main()
{
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++)
scanf("%lld",&v[i]);
for(int x,y,i=1;i
1007 Circle
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 0 Accepted Submission(s): 0
Problem Description
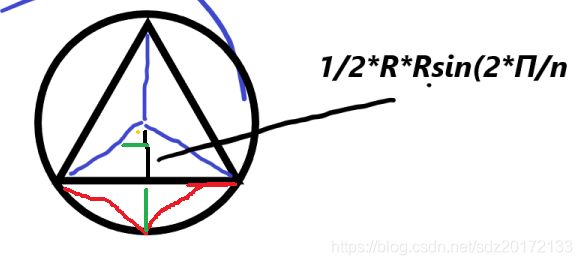
在半径为 1 的圆上有 n 个点,它们也是圆的 n 等分点,将每个相邻的 n 等分点相连,组成了一个正 n边形,现在你可以在圆上再增加一个点,使得新的 n + 1 边形的面积最大,请输出最大面积。
Input
输入有多组(不超过 100 组)。
每组数据一行一个整数 n 代表点的数量。
3 ≤ n ≤ 100
Output
每组数据输出一行一个数表示加上一个点后的最大面积,结果保留6位小数。
Sample Input
3
Sample Output
1.732051
Source
755hdu女生赛
分析:圆的正接多边形的面积为n *1/2*R*Rsin(2*Π/n){可以分为n个三角形,证弦公式s=1/2*a*b*sin∠ab),再加一个点就是新加一个等腰三角形,边长为:2*R*sin(PI/n) 高=(R-R*cos(PI/n));
总之,这题巧妙的用来余弦和正弦定理
#include
using namespace std;
typedef long long ll;
const int N=500005;
const int MOD=1e9+7;
const double PI = acos(-1.0);
int main()
{
int n;
while(scanf("%lld",&n)!=-1)
{
double ans=n*sin(2.0*PI/n)/2.0+(2.0*sin(PI/n))*(1.0-cos(PI/n))/2.0;
printf("%.6lf\n",ans);
}
return 0;
}
题目:
1008 Clock
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 0 Accepted Submission(s): 0
Problem Description
wls 有一个钟表,当前钟表指向了某一个时间。
又有一些很重要的时刻,wls 想要在钟表上复现这些时间(并不需要依次复现)。我们可以顺时针转动秒针,也可以逆时针转动秒针,分针和时针都会随着秒针按规则转动,wls 想知道秒针至少转动多少角度可以使每个时刻至少都会被访问一次。
注意,时钟上的一种时针分针秒针的组合,可以代表两个不同的时间。
Input
第一行一个整数 n 代表有多少个时刻要访问。
第二行三个整数 h,m,s 分别代表当前时刻的时分秒。
最后n行每一行三个整数 hi,mi,si 代表每个要访问的时刻的时分秒。
1 ≤ n ≤ 86, 400
0 ≤ h, hi < 24
0 ≤ m, mi, s, si < 60
Output
输出一行一个数代表秒钟转的角度,答案保留两位小数。
Sample Input
1
0 1 0
0 1 1
Sample Output
6.00
总共可以分为四种情况:只顺时针转,只逆时针转,先顺时针再逆时针,先逆时针再顺时针。
所以的情况直接暴力模拟就行,对于后面两种情况对每次顺时针和逆时针结束的终点进行枚举然后求出值。注意:每一个时间都是一个对象,包含距离给出的顺时针角度和逆时针角度。
#include
#define INF 0x3F3F3F3F
using namespace std;
typedef long long ll;
const int maxn=1e5+5;
int n,m;
int t;
int tn(int x)
{
int z=x%12;
return z;
}
struct node
{
int shun;
int ni;
int a,b,c;
int num;
} dian[90000];
int tim(int h,int m,int s)
{
int zz=h*3600+m*60+s;
return zz;
}
bool comp(node a,node b)
{
return a.shun0)
{
dian[cnt].shun=kk;
dian[cnt].ni=43200-dian[i].shun;
cnt++;
}
if(kk==0)
{
continue;
}
}
}
sort(dian+1,dian+cnt,comp);
int mi=INF;
int ss=dian[cnt-1].shun; //全顺
mi=min(ss,mi);
ss=dian[1].ni; //全逆
mi=min(ss,mi);
for(int i=1; i<=cnt-1; i++) //枚举先顺后逆的讨论
{
int summ=0;
summ=summ+dian[i].shun*2+dian[i+1].ni;
mi=min(mi,summ);
}
for(int i=cnt; i>=2; i--)
{
int summ=0;
summ+=dian[i].ni*2+dian[i-1].shun;
mi=min(mi,summ);
}
double fin=(double)mi*1.0*6.00;
printf("%.2lf\n",fin);
return 0;
}
1010 Tangram
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 0 Accepted Submission(s): 0
Problem Description
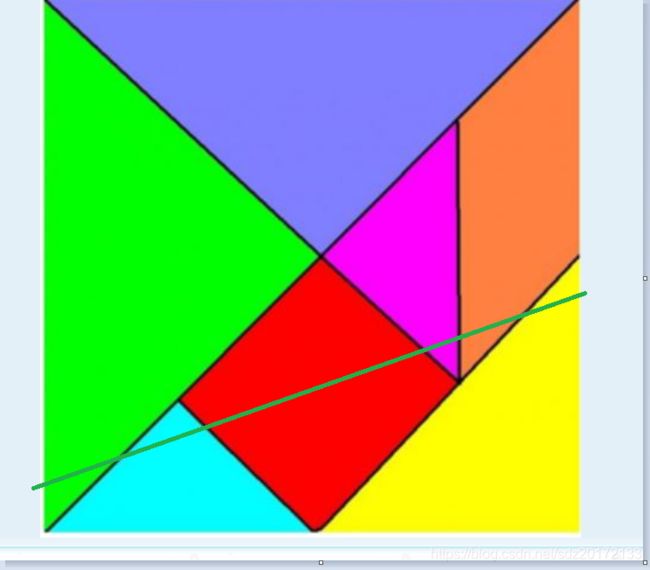
一块七巧板有 7 块,现在 wls 想再在七巧板上加 n 条直线将七巧板切分并且使得切出来的块最多,请问最多能有多少块?
![]()
Input
输入有多组(不超过 100, 000组)。
每组一行一个正整数 n。
0 ≤ n ≤ 1, 000, 000, 000
Output
每组输出一行一个数代表答案。
Sample Input
1
Sample Output
13
Source
755hdu女生赛
分析:加一条线:7+6
加两条线:7+6+7
以此类推即可
#include
using namespace std;
typedef long long ll;
const int N=500005;
const int MOD=1e9+7;
int main()
{
ll n;
while(scanf("%lld",&n)!=-1)
{
ll ans=7;
ans+=(n)*(6+6+n-1)/2;
printf("%lld\n",ans);
}
return 0;
}
1011 Tetris
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 524288/524288 K (Java/Others)
Total Submission(s): 0 Accepted Submission(s): 0
Special Judge
Problem Description
wls 有一个 n ∗ m 的网格,他现在想用俄罗斯方块中的"凸"型密铺它。
![]()
一个"凸"型占四个格子,你可以随意把它调成上下左右四个方向中的一个。
密铺的定义是网格中任意一个格子被且只被一个"凸"型铺到,并且这些"凸"型不能铺出网格的边界。
随意输出一组解即可。
Input
一行两个整数 n, m。
1 ≤ n, m ≤ 12
Output
无解输出 no response。
如果有解,输出 n 行,每行 m 个字符。你只能使用 1, 2, 3, 4 这四个字符,由同一字符组成的四连通块被视为一个"凸"型。
如果有多组解,那么输出任意一种即可。
Sample Input
4 4
Sample Output
1113 2133 2243 2444
Source
755hdu女生赛
可以发现只有n和m都为4的倍数才有解。
#include
using namespace std;
typedef long long ll;
const int N=500005;
const int MOD=1e9+7;
const double PI = acos(-1.0);
int a[100][100];
int b[10][10];
string s[100];
int main()
{
s[0]="1113111311131113111311131113";
s[1]="2133213321332133213321332133";
s[2]="2243224322432243224322432243";
s[3]="2444244424442444244424442444";
s[4]="1113111311131113111311131113";
s[5]="2133213321332133213321332133";
s[6]="2243224322432243224322432243";
s[7]="2444244424442444244424442444";
s[8]="1113111311131113111311131113";
s[9]="2133213321332133213321332133";
s[10]="2243224322432243224322432243";
s[11]="2444244424442444244424442444";
s[12]="1113111311131113111311131113";
s[13]="2133213321332133213321332133";
s[14]="2243224322432243224322432243";
s[15]="2444244424442444244424442444";
int n,m;
while(scanf("%d%d",&n,&m)!=-1)
{
if(n%4==0&&m%4==0)
{
for(int i=0; i