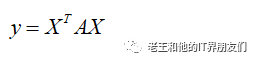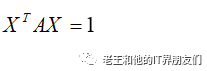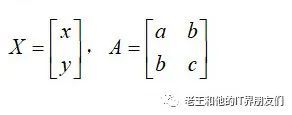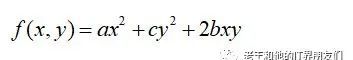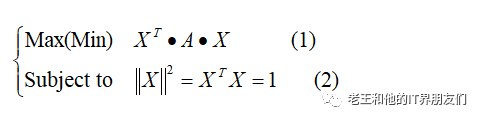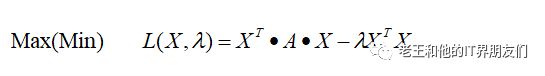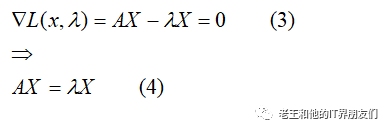PCA主成分分析（下）

 

作者：赵蕾

---

美，是在高潮处陡然消逝，不落凡尘。

数学中的美，是不是也是寻找那个导数为零的极值点？

实际问题中，我们认为凸型函数是函数中是相对完美而且最容易求极值点的。

哦……可惜数学实际上没那么多想象的浪漫，它的极致应如潜入深海之渊，耐得住寂寞，踏实严谨。

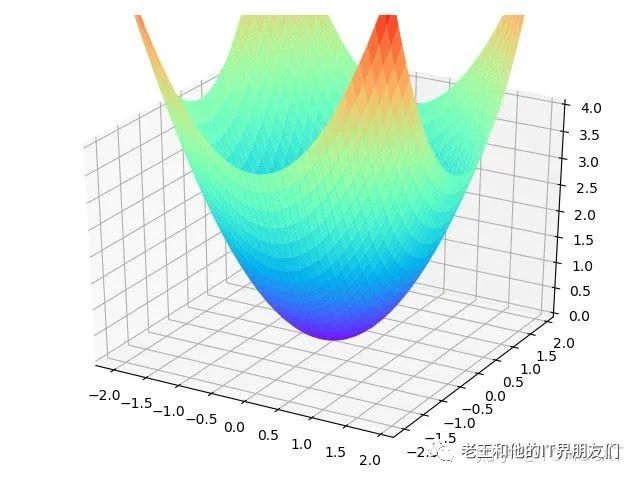
所以上图不是凸函数，相反，它叫凹函数。凹凸函数定义如下图：

在2维空间内，凸函数类似于这样的二次函数

其中：

显然，实际问题若符合凸函数性质，往往方便求出其极小值。

在机器学习过程中，衡量一个分类（判断问题）或回归（拟合问题）是否精确的，就是取得这些损失函数的极小值。

而损失函数，如对数损失函数、平方损失函数，都是凸函数，探求凸函数的“谷底”，就是我们追求的目标。

但是机器学习处理的往往是高维数据，所以，将上述一元二次函数，扩展到多维空间的多元二次型。标量x被向量X(x1,x2,x3....xn)替代，系数a被代替矩阵A，依然得到一个凸函数：

其中

即：A为正定矩阵（特征值全部大于0）

考虑多元二次型的实际意义，我们先从包含两个变量(x,y)的二次型出发。

形如：

的方程，可以表示为：

其中：

我们得出：

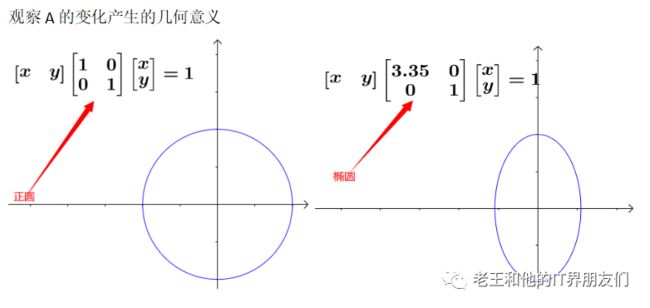
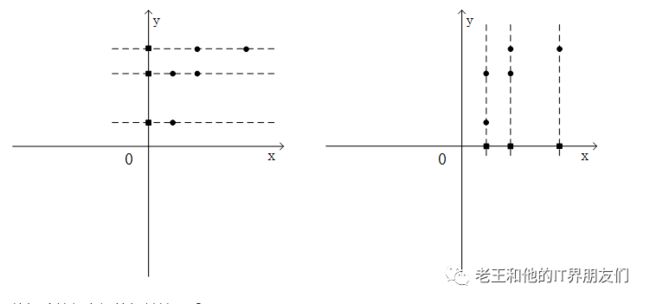
1. 二次型矩阵A，若是一个对角矩阵，对角线上的元素值，决定了图形的形状。

2. 左图的A决定了图形为正圆，右图则为椭圆

3. 两个图像具有线性（拉伸）关系，即通过变换二次型矩阵A，将正圆拉伸为椭圆。

4. 但是线性变换，只有拉伸，没有旋转。

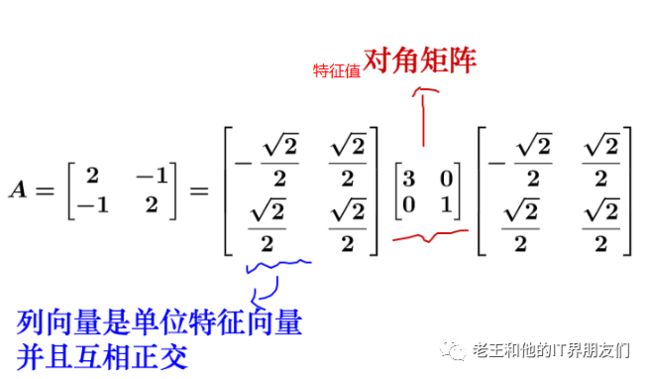
再来变换：

两边乘以正交向量，令：

得到一个旋转后拉伸后的圆——倾斜椭圆

实际上：

现在，借助二次型矩阵A，我们又可以将函数

表示回

进一步分析问题前，先来考虑y的极值问题。

 

我们已经知道上述二次型符合凸函数性质，实际中凸函数的极值问题，往往是带约束的求极值问题，也就是说我们要在求极值的同时加上一个条件——凸优化问题

 

比如在X的2范式——X的长度——为1的情况下，求上述二次型的极值。情况变成这样

 

就是我们要在（2）的条件下求（1）的极大/小值。带入拉格朗日乘数，将上述问题归结为以下函数的极值问题：

类比一元函数的极值问题，我们求L的梯度，令梯度为0。得出

当（4）式成立，我们得到原式（1）的极值，故将结果式（4）带入（1），原问题为

又根据约束条件，式（2）

故极值问题又可化解为

它就是A的特征值，也就是说，求二次型（1）的最大最小，最终归结为，求二次型矩阵A最大最小特征值的问题。

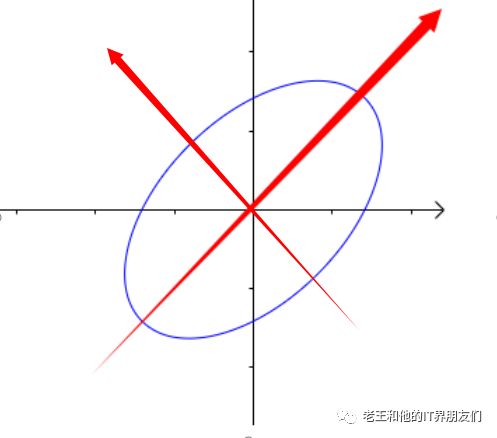
回忆二次型矩阵的几何意义。对于二次型矩阵A，特征值就是图形进行伸缩的量，对应特征向量的就是图形旋转的方向。

而对称矩阵的特征向量两两正交，实际上正是构成了旋转后的坐标方向。

 

总结：求二次型的极值问题，就是求二次型矩阵特征值极值问题，就是求一个原始球在旋转后的空间中最大/最小拉伸。而这个特征值对应的特征向量，就是球最大/最小拉伸的方向。就是旋转后新的坐标轴

问题分析到这里，我们引出了特征值，似曾相识。

PCA就是利用了协方差矩阵的较大特征值，得到坐标旋转变换后，保留数据点最大拉伸（最分散）的那个坐标“轴”，即最佳数据投影方向。

为什么要使数据点最分散？

因为数据点压缩后集中到一起，如果重合为一点，那么信息就会严重受损。如下图

压缩后数据点的分散程度，决定了我们保留原信息的程度。

 

下篇，我们接着分析PCA压缩数据的实质出发，引入求二次型极值问题，最终套用今天的分析结果。使得分解协方差矩阵得最大特征值从而解决原始数据降维问题。

 

未完结，其实是一篇放不下