NOIP2018PJ
前言
嘛现在或许晚了点。。。水题的时候兴致一来就顺手切了(嘛也不是随手
嗯,就这样
题解
T1 标题统计
题目描述
凯凯刚写了一篇美妙的作文,请问这篇作文的标题中有多少个字符?
注意:标题中可能包含大、小写英文字母、数字字符、空格和换行符。统计标题字符数时,空格和换行符不计算在内。
⋯ \cdots ⋯
Var s:string[10];
tot,i:longint;
Begin
readln(s);
tot:=0;
for i:=1 to length(s) do
Begin
if s[i] in ['A'..'Z','a'..'z','0'..'9'] then
Begin
inc(tot);
end;
end;
write(tot);
end.
T2 龙虎斗
题目描述
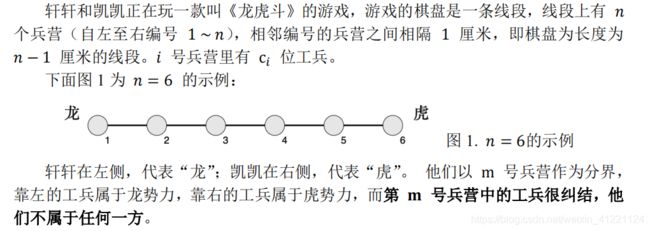

暴力一遍把 S 2 S_2 S2位工兵放置在每个位置,使得差距最小化
Var n,m,p1,s1,s2,tot1,tot2,disparity,temp,pos,deposit:int64;
i:longint;
c:array[1..100005] of int64;
Begin
readln(n);
for i:=1 to n do
Begin
read(c[i]);
end;
readln(m,p1,s1,s2);
c[p1]:=c[p1]+s1;
for i:=1 to m-1 do
Begin
tot1:=tot1+c[i]*(m-i);
end;
for i:=m+1 to n do
Begin
tot2:=tot2+c[i]*(i-m);
end;
disparity:=abs(tot2-tot1);
deposit:=disparity;
for i:=1 to m-1 do
Begin
temp:=abs(tot2-(tot1+s2*(m-i)));
if temp<disparity then
Begin
disparity:=temp;
pos:=i;
end;
end;
for i:=m+1 to n do
Begin
temp:=abs(tot2+s2*(i-m)-tot1);
if temp<disparity then
Begin
disparity:=temp;
pos:=i;
end;
end;
if disparity=deposit then
Begin
write(m);
end
else
Begin
write(pos);
end;
end.
T3 摆渡车
题目描述
有 n 名同学要乘坐摆渡车从人大附中前往人民大学,第 i 位同学在第 ti 分钟去等车。只有一辆摆渡车在工作,但摆渡车容量可以视为无限大。摆渡车从人大附中出发、把车上的同学送到人民大学、再回到人大附中(去接其他同学),这样往返一趟总共花费 m 分钟(同学上下车时间忽略不计)。摆渡车要将所有同学都送到人民大学。
凯凯很好奇,如果他能任意安排摆渡车出发的时间,那么这些同学的等车时间之和最小为多少呢?
注意:摆渡车回到人大附中后可以即刻出发。
dalao说可以用斜率优化,但是嘛没必要
我承认我不会斜率优化…
很显然,状态转移方程为:
f i = m i n ( f i , f j + ( t o t i − t o t j ) × i − ( s u m i − s u m j ) ) ; f_i=min(f_i,f_j+(tot_i-tot_j)\times i-(sum_i-sum_j)); fi=min(fi,fj+(toti−totj)×i−(sumi−sumj));
其中
t o t i tot_i toti为第直至 i i i个时间点的人数和
s u m i = ∑ i = 1 n t i sum_i=\sum\limits_{i=1}^{n}t_i sumi=i=1∑nti
f i f_i fi表示至 i i i的最小等待时间
于是乎很快就可得出核心程序:
for (int i=0; i<time+m; i++){
f[i]=tot[i]*i-sum[i];
int ST=fmax(i-2*m+1,0);
for (int j=ST; j<=i-m; j++){
f[i]=fmin(f[i],f[j]+(tot[i]-tot[j])*i-(sum[i]-sum[j]));
}
}
for (int i=time; i<time+m; i++){
minAns=minAns<f[i]?minAns:f[i];
}
但是时间复杂度显然是超出了限制,
那么这段程序如何优化呢,
其实很容易就可以想到,这么长的一条时间轴,只有 n ≤ 500 n\leq500 n≤500个点是需要取的,况且这些点中还有不少是重合的,由此可得知这些点是离散得十分严重的,那么的话如果把所有的点都遍历一遍显然是不可取的。
那么这就需要加上一个判断了:当当前的 i i i到 i − m i-m i−m中没有人的话,把 f i − m f_{i-m} fi−m的状态转移到 f i f_i fi即可
AC完整代码:
#includeT4 对称二叉树
题目描述

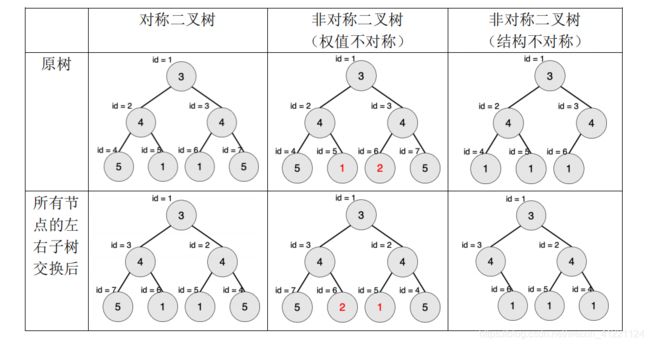

如果暴力遍历来判断两个子树 x x x和 y y y是否对称,最坏的情况下要遍历 2 ∗ m i n ( s i z e [ x ] , s i z e [ y ] ) 2*min(size[x],size[y]) 2∗min(size[x],size[y]) 个点。
很显然的,可以分析出总复杂度为 O ( n l o g n ) O(n log n) O(nlogn)
故暴力搜索即可
附上代码:
uses math;
Var n,i,j,ans:longint;
weight,temp:array[1..1000005] of longint;
Sub:array[1..1000005] of record
left,right:longint;
end;
Function get_validity(x,y,z:longint):boolean;
Begin
if weight[y]=weight[z] then
Begin
if (Sub[y].left*Sub[z].right<0) or (Sub[y].right*Sub[z].left<0) then
Begin
exit(false);
end
else if ((Sub[y].left=-1) or (get_validity(x,Sub[y].left,Sub[z].right))) and ((Sub[y].right=-1) or (get_validity(x,Sub[y].right,Sub[z].left))) then
Begin
exit(true);
end;
end;
exit(false);
end;
Procedure get_total(x:longint);
Begin
if Sub[x].left<>-1 then
Begin
get_total(Sub[x].left);
temp[x]:=temp[Sub[x].left];
end;
if Sub[x].right<>-1 then
Begin
get_total(Sub[x].right);
temp[x]:=temp[x]+temp[Sub[x].right];
end;
temp[x]:=temp[x]+1;
end;
Begin
readln(n);
for i:=1 to n do read(weight[i]);
for i:=1 to n do read(Sub[i].left,Sub[i].right);
get_total(1);
ans:=1;
for i:=1 to n do
Begin
if (Sub[i].left<>-1) and (Sub[i].right<>-1) and (get_validity(i,Sub[i].left,Sub[i].right)) then
Begin
ans:=max(temp[i],ans);
end;
end;
write(ans);
end.