小白入门中：TCPL习题2-1——2-10

2-1：编写程序确认signed和unsigned限定的char、short、int与long类型变量的取值范围。采用打印标准头文件中的限定值或直接计算。

#include 
#include 
#include 
int main()
{
	printf("打印signed与unsiged限定的变量取值范围\n");
	printf("char:\n");
	printf("The max value of char is %d\n" , CHAR_MAX );	//signed char
	printf("The min value of char is %d\n" , CHAR_MIN );
	printf("The max value of unsigend char is %u\n" , UCHAR_MAX );	//unsigned char

	printf("int:\n");
	printf("The max value of int is %d\n" , INT32_MAX );	//signed int
	printf("The min value of int is %d\n" , INT32_MIN );
	printf("The max value of unsigend min is %lu\n" , UINT32_MAX );	//unsigned int

	printf("short:\n");
	printf("The max value of short is %d\n" , SHRT_MAX );	//signed short
	printf("The min value of short is %d\n" , SHRT_MIN );
	printf("The max value of unsigend short is %lu\n" , USHRT_MAX );	//unsigned short

	printf("long:\n");
	printf("The max value of long is %ld\n" , LONG_MAX );	//signed long
	printf("The min value of long is %ld\n" , LONG_MIN );
	printf("The max value of unsigend long is %lu\n" , ULONG_MAX );	//unsigned long
	system("pause");
	return 0 ;
}
}

2-2：在不使用&&或||的条件下编写一个与下面的for循环语句等价的循环语句

• for(i=0 ; i

#include
#include 
#include 
#define lim 100
int main()
{	
	int i ;
	char c , s[lim];
	enum flag{no , yes}conditon;
	//循环实现
	i = 0 ;
	conditon = yes ;
	while (conditon == yes)
	{
		if(i >= lim - 1) conditon = no;
		else if ((c = getchar()) == '\n') conditon = no ;
		else if (c == EOF) conditon = no ;
		else 
		{
			s[i] = c ;
			i ++ ;
		}
	}
	s[i] = '\0'; //重点
	printf("%s\n" , s );
	system("pause");
	return 0 ;

}

enum枚举变量，no = 0 ， yes = 1；
注意末尾要加一个s[i] = '\0';，不然会多输出2~4个随机字符；

2-3：编写一个函数htoi(s),把由16进制数组组成的字符串（包含可选的前缀0x或0X） 转换为与之等价的整型值，字符串中允许包含的数字包括：0-9、a-f，A-F

#include
#include 
#include 
/*编写一个函数htoi(s),把由16进制数组组成的字符串（包含可选的前缀0x或0X）
  转换为与之等价的整型值，字符串中允许包含的数字包括：0-9、a-f，A-F*/
int htoi(char s[])
{
	int num ; 
	sscanf(s , "%x" , &num);
	return (int)num;
}
int main()
{	
	char line[100];
	int num ; 
	while (1)
	{
		gets(line);
	 	num = htoi(line);
	 	printf("%d\n" , num);
	}
	system("pause");
	return 0 ;

}

这是我的思路，将字符串中表示16进制的字符串，以16进制的形式存储到num中，然后用（int）直接转换为整形；
运行：

hhh还是可以的，不过感觉有些作弊，这可以作为一个16转10的好办法
以下为题解所给的代码

#define yes 1
#define no  0
int htoi(char s[])
{
	int hexdigit , i , inhex , n ; 
	i = 0;
	if(s[i] == '0')					//假如字符串有16进制前缀 0x 或 0X ；
		i ++ ;
	if(s[i] == 'x' || s[i] == 'X')
		i ++ ;
	n = 0 ; 
	inhex = yes ; 
	for( ; inhex == yes ; ++i)
	{
		if(s[i]>= '0' && s[i] <= '9')
			hexdigit = s[i] - '0';
		else if(s[i] >= 'a' && s[i] <= 'f')
			hexdigit = s[i] - 'a' + 10 ; 
		else if(s[i] >= 'A' && s[i] <= 'F')
			hexdigit = s[i] - 'A' + 10 ;
		else inhex = no ;
		if(inhex == yes)
		{
			n = n*16 + hexdigit ;
		}
	}
	return n ;
}

其中最精妙的就是这一步n = n*16 + hexdigit
举例子，ABCD = 43981
ABCD分别对应10 11 12 13;
根据进制转换

sum = 13*16^0 + 12*16^1 + 11*16^2 + 10*16^4
	= {[(10*16+11)*16+12]*16+13}
这就跟上面的式子是一致的

第一种思路在解决8转10，16转10较为方便%o，%x，但在其他就会出错。
第二种在解决除8,16外只需修改几个数字就可以得出答案。

2-4：重新编写squeeze(s1 , s2)，将S1中任何与S2中的字符匹配的字符都删除

#include
#include 
#include 
#define yes 1
#define no  0
/*重新编写squeeze(s1 , s2)，将S1中任何与S2中的字符匹配的字符都删除*/
int squeeze(char s1[] , char s2[])
{
	int i , j , k ;
	for(i=k=0 ; s1[i] != '\0' ; i++)
	{
		for(j=0 ; s2[j]!='\0' && s2[j] != s1[i] ; j++ )
			;
		if(s2[j] == '\0')
		{
			s1[k++] = s1[i] ;
		}
	}
	s1[k] = '\0' ;
}
int main()
{	
	char line1[100] , line2[100];
	int num ; 
	while (1)
	{
		gets(line1);
		gets(line2);
		squeeze(line1 , line2);
	 	printf("%s\n" , line1);
	}
	system("pause");
	return 0 ;

}

我勒个去，又忘记写s1[k] = '\0';谨记谨记，字符串的末尾必为'\0'

2-5：编写函数any(s1 , s2),返回s2任意字符第一次出现在s1的位置，若s1中没有s2的字符，则返回-1。（标准库函数strpbrk具有同样的功能，但它返回的是指向该位置的指针）**

#include
#include 
#include 
#define yes 1
#define no  0
/*重新编写squeeze(s1 , s2)，将S1中任何与S2中的字符匹配的字符都删除*/
int squeeze(char s1[] , char s2[])
{
	int i , j , condition , flag = -1 ;
	condition = yes ;
	for(i=0 ; s1[i] != '\0' && condition ; i++)
	{
		for(j=0 ; s2[j] != '\0' ; j++)
		{
			if(s1[i] == s2[j])
			{
				flag = (i + 1);
				condition = no ;
			}
		}
	}
	return flag ;
}
int main()
{	
	char line1[100] , line2[100];
	int num ; 
	while (1)
	{
		gets(line1);
		gets(line2);
		num = squeeze(line1 , line2);
	 	printf("%d\n" , num);
	}
	system("pause");
	return 0 ;
}

2-6：编写一个函数setbits(x , p , n , y)，返回对x执行操作的结果值：将x中从第p位开始的n个（二进制）位设置为y中最右边n位的值，x的其余各位保持不变**

#include 
#include 
using namespace std;
/*编写一个函数setbits(x , p , n , y)，返回对x执行操作的结果值：
将x中从第p位开始的n个（二进制）位设置为y中最右边n位的值，x的其余各位保持不变*/
int setbits(unsigned x , int p , int n , unsigned y );
int main()
{
	int  p ,  n , result;
	unsigned int x , y ;
	while(cin >> x >> p >> n >> y)	//输出x , p , n , y
	{
		result = setbits(x , p , n , y) ;
		cout << result << endl ; 
	}	
	system("pause");
	return 0 ;
}
//假设最右为第0位
int setbits(unsigned x , int p , int n , unsigned y )
{
	unsigned a , b ; //a用于保存x中从p开始n位的值,b保存y除最右边n位的值
	a = (x >> (p+1-n)) & ~(~0 << n) ;
	b = (~0 << n) & y ;
	return  a + b ;
}

假设最右为第0位
46：
0101110
75：
1001011
5位开始3位，即5、4、3位，101；
1001101为77
（ps.答案是真的鸡儿诡异，还是哥的思路好）

2-7：编写一个函数invert(x , p , n)，返回对x执行操作的结果值：将x中从第p位开始的n个（二进制）位求反，x的其余各位保持不变**

#include 
#include 
using namespace std;
/*编写一个函数invert(x , p , n)，返回对x执行操作的结果值：
将x中从第p位开始的n个（二进制）位求反，x的其余各位保持不变*/
int invert(unsigned x , int p , int n );
int main()
{
	int  p ,  n , result;
	unsigned int x ;
	while(cin >> x >> p >> n )	//输入x , p , n  
	{
		result = invert(x , p , n) ;
		cout << result << endl ; 
	}	
	system("pause");
	return 0 ;
}
//假设最右为第0位
int invert(unsigned x , int p , int n )
{
	unsigned a , b , c; //a保存除第p位开始n位的位，b保存x中第p位开始的n位的反转
	/*
	假设43: 00101011 , p=5, n=2 , 为 10
	a = 00001011 ;  --> 11111111 --> 11111100 --> 00000011 --> 00110000 --> & x --> ^ 0011000		
	b = 00010000 ;  --> 11111111 --> 11111100 --> 00000011 --> 00110000 --> 11001111 --> & x	
	(~(~0 << n) << (p+1-n)) : 00110000
	*/
	c = (~(~0 << n) << (p+1-n)); //c : 00110000 ;
	a = (c & x) ^ c ; //a = 00010000
	b = ~c & x; //b = 00001011
	return a + b ;
}

（ps. 注释写得好，思路没烦恼，原本的a， b是一串诡异的表达式，写着写着自己就乱了。于是定义了c = (~(~0 << n) << (p+1-n)); //c : 00110000 ;，表明了注释，果然通透明了许多）

编写一个函数invert(x , p , n)，返回对x执行操作的结果值： 将x右移n次，溢出的值补到高位

#include 
#include 
using namespace std;
/*编写一个函数invert(x , p , n)，返回对x执行操作的结果值：
将x右移n次，溢出的值补到高位*/
int rightrot(unsigned x , int p);
int length(void);
int main()
{
	int  p ;
	unsigned int x , result;
	cout << "计算机所使用的位长度为 ：" ;
	cout << length() << endl;
	while(cin >> x >> p)	//输入x , p 
	{
		result = rightrot(x , p);
		cout << result << endl ; 
	}	
	system("pause");
	return 0 ;
}
//假设最右为第0位
int rightrot(unsigned x , int p)
{
	int length(void);
	unsigned a , b ;
	while (p--)
	{
		a = (x & 1) << (length() - 1) ;//把x的最右位移到
		x = x >> 1 ;
		x = x | a ;
	}
	return x ;
}
int length(void) //求出计算机所使用的位长度
{
	int i ;
	unsigned v = (unsigned) ~0;
	for(i=1 ; (v = v >> 1) > 0 ; i++)
		;
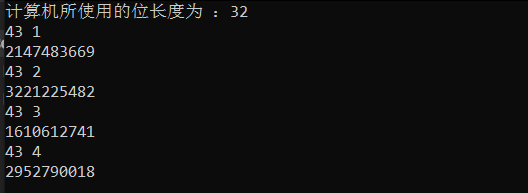
	return i ;
}

a = (x & 1) << (length() - 1)这一步确实没想到，length函数也是精妙，用>>求出所有位，学到了。

2-9：求二进制补码时，表达式 x&=(x-1)可以删除x中最右边值为1的一个二进制位，请解释原理。用这一方法重写bitscount函数，以加快执行速度

int bitscount(unsigned x)
{	
	int i ;
	for(i = 0; x != 0; x >>= 1)
	{
		if(x & 1) i++ ;
	}
	return i ;
}

原理：x-1，二进位中最右是1的位必然要退1，即为0，在&运算中，原本的最后一位x位1，x-1为0，结果为0
即1被删去了！！！
（语言表述可能有误，但大致是这样）

#include 
#include 
using namespace std;
/*求二进制补码时，表达式 x&=(x-1)可以删除x中最右边值为1的一个二进制位，请解释原理
用这一方法重写bitscount函数，以加快执行速度
*/
int re_bitscount(unsigned x);
int length(void);
int main()
{
	int  p ;
	unsigned int x , result;
	cout << "计算机所使用的位长度为 ：" ;
	cout << length() << endl;
	while(cin >> x)	//输入x
	{
		result = re_bitscount(x);
		cout << result << endl ; 
	}	
	system("pause");
	return 0 ;
}
//假设最右为第0位
int re_bitscount(unsigned x)
{
	int count;
	for(count = 0; x > 0; x &= (x-1))
		count++;
	return count ;
}
int length(void) //求出计算机所使用的位长度
{
	int i ;
	unsigned v = (unsigned) ~0;
	for(i=1 ; (v = v >> 1) > 0 ; i++)
		;
	return i ;
}

2-10：重新编写将大写字母转为小写字母的函数lower，用条件表达式替代if-else结构

#include 
#include 
using namespace std;
/*重新编写将大写字母转为小写字母的函数lower，用条件表达式替代if-else结构
*/
int lower(char AAs);
int main()
{
	char a ; 
	while((a = getchar()) != EOF)	
	{
		a = lower (a) ;
		cout << a  ;
	}	
	system("pause");
	return 0 ;
}
int lower (char s)
{
	return (s >= 'A' && s <= 'Z') ? s - 'A' + 'a' : s ;
}

总结：类型、运算符与表达式

讲道理，这个章节是很烦人的。首先是以处理字符串问题练习关系运算符、逻辑运算符，当然，也把字符串熟悉了一下。更加深入地了解了字符串数组，'\n' , '\0'什么的我之前都是懵懵懂懂。
到后面就是烦人的位运算符了，因为书看不懂所以放弃了摸鱼了两天（实际上是在策划学院比赛，有点紧张，学不下去，对吧对吧对吧），后在4.29时候认真学习了一哈位运算符，可以说是初步掌握。特别是x &= (x-1)这个骚操作求二进制位上1的个数，属实牛逼。我想位运算符应该还有更多骚气的操作。不过我要思考的不是位运算符还能解决什么问题，而是有什么问题用位运算符解决会更加方便，不要搞花里胡哨，而要追求实际！！
明天学习第三章控制流，加油，奥利给，干就完事了！！