线性表
写在前面
打算写一下关于数据结构和算法中的一些学习笔记,在文档中只会用C语言进行算法和数据结构的实现。参考书籍《数据结构与算法(C语言版)》(严蔚敏)
一、什么是数据结构
按照课本上的概念,数据结构是相互之间存在的的一种或者多种特定关系的数据元素的集合。但是这样理解有点抽象,我认为可以将数据结构理解为同类型数据的集合和关系的描述。比如线性表就是相同类型元素按照线型结构存储的一种数据结构。
二、为什么需要数据结构
我在学习C++的时候写过一些简单的小程序和一些MFC程序,但是从没有接触过这些也能写出来,当时我也很疑惑为什么需要学习数据结构,这不应该是那些写底层的人考虑的吗,但是后来我明白了数据结构不是线性表,队列,也不是树,更不是图,而是来自于我们生活中的一种思想。数据结构中涉及的一些基本操作如果你不写代码只想的话会感觉有带你stupid,但是当你尝试将这些问题代码化的时候一切都不那么简单。
我个人认为数据结构与算法教会了我编程的思维模式(可能有点夸张),但是我的确受益良多,因此打算写一些笔记,一方面供今后参考,一方面看了那么多网上的资料,也想写一点自己的为和自己思维方式一样的人提供好的参考文档,在笔记中我不会太多纠结于概念性的问题,我尽量将代码作为重点。
三、算法性能的描述
时间复杂度:它定量描述了该算法的运行时间。一般用O(n)表示。
空间复杂度:是对一个算法在运行过程中临时占用存储空间大小的量度,记做S(n)=O(f(n))。
比如最简单的按值查找算法并未使用外部空间存储程序所用到的数据,程序中用到的数据基本来自于程序外,因此空间复杂度为O(1);而时间复杂度可分为最坏时间复杂度,最佳时间复杂度和平均时间复杂度,对于该算法分别为O(n)(要遍历整个线性表),O(1)(第一次就找到),O(n)。
线性表
一、线性表的概念和基本操作
1、线性表的概念
线性表是具有n(n>0)个相同元素的有限序列的集合。线性表除了第一个元素,每一个元素都有一个直接前驱,除了最后一个元素每一个都有一个直接后继。
线性表一般可以表示为L=(a~1,a~2,a~3,…,a~n-1)。
2、线性表的基本操作
一般线性表的基本操作有增、删、查、改,而一个完整的线性表的定义的基本操作有以下几种:
- InitList(&L) 初始化操作
- DestroyList(&L) 销毁操作
- ClearList(&L) 清空线性表
- ListEmpty(L) 判断为空
- ListLength(L) 获取长度
- GetElem(L, i, &e) 获取第i个元素
- LocateElem(L, e, compare) 获取第一个符合compare的元素
- PriorElem(L, cur, &pre) 获取前驱
- NextElem(L, cur, &next) 获取后继
- ListInsert(&L, i ,e) 将元素e插入到i处
- ListDelete(&L, i, &e) 删除第i个元素并存入e
- ListTraverse(L, visit()) 以visit函数遍历线性表
二、线性表的分类
1、顺序线性表
定义和特点
顺序线性表是指一组地址连续的存储单元依次存储线性表的数据元素的结构。简单的说就是表中的元素在内存中的地址是连续的,这就意味着可以通过一定的关系进行定位。
比如a_1是线性表的第一个元素LOC表示对元素进行取地址,size表示线性表中单个元素的大小那么第i个元素ai的地址为:
LOC(a_i) = LOC(a_1) + size * (i - 1)
顺序线性表的特点就是利用上述方式进行随机存取,这也是顺序表的一大优点,缺点是对内存的要求比较大,当顺序表太大时就需要很大一块连续的内存,而且插入和删除不方便。
下面我举个简单的例子说明,无论什么语言数组都是必需的,假定有下面一个数组a[7]:
数组中分别存储着1,2,3,4,5,6,7几个元素,一般我们可以通过a[i]来获取对应单元的数据元素,原理就是上面提到的式子,它会以a[0]为基准i*sizeof(ElemType)为偏移量计算出对应元素的地址再取值。
数据结构定义
静态内存分配
需要的内存一次性分配,与系统自动管理生成和回收,使用方便,但须预先知道要使用的内存大小,生成后无法改变。
#define MAX_SIZE 100 //线性表的长度
typedef int ElemType; //线性表内的数据类型
typedef struct
{
ElemType data[MAX_SIZE]; //数据存储区域
int length; //已存储数据的长度
}sqList;动态内存分配
由用户通过malloc()(C语言中)申请生成,也有用户自行管理包括回收,有一定的危险性(内存泄漏),但是内存的长度相对没有限制(当然也受硬件大小的限制)可自由分配。
#define INIT_SIZE 100 //初始化线性表的长度
#define INCREASE_SIZE 50 //当线性表内存占满时的增量
typedef int ElemType; //线性表内的数据类型
typedef struct
{
ElemType* data; //数据指针
int length,maxSize; //length为已存储的数据长度,maxSize为已分配的内存空间大小
}sqList;2、链式线性表
链式线性表的特点是元素与元素之间的物理地址没有特定的规律,也就解除了线性表对物理内存连续性的限制,但是为了维护元素与元素之间的关系为每一个元素提供了一个指针指向他的后继。结构图如下:
图示为一个单链表,其中L为链表的头是为了方便后续操作而添加的,当然也可以没有链表的每个结点维护一个指针和数据域,数据域存储相关数据,指针用来连接结点。链表在插入方面拥有强大的性能,可以很方便的进行插入,并且单链表不对内存空间的连续性做要求,因此存储很灵活;但是无法随机存取,需要从第一个节点开始遍历,另外内存利用率不如顺序表,因为他维护了一个指针来建立结点之间的联系。
单链表的结构定义
typedef int ElemType;
typedef struct ListNode
{
ElemType data;
struct ListNode* next;
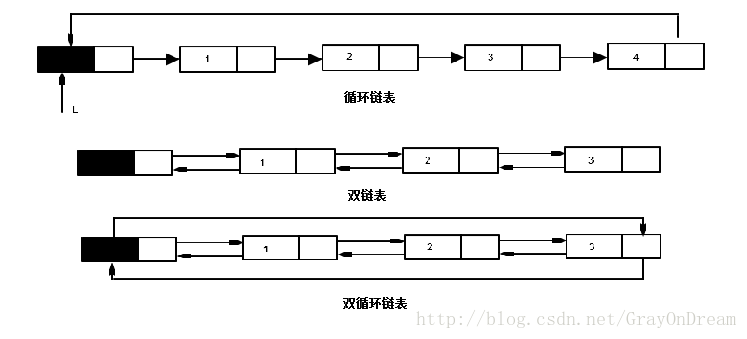
}ListNode, *LinkList;链表不止单链表还有双链表,循环链表,和双循环链表,基本思想一致,循环链表是末尾的指针指向做了改变,而双链表是多维护了一个指针指向结点的前驱。
双链表的定义
typedef int ElemType;
typedef struct ListNode
{
ElemType data;
struct ListNode* next,*prior;
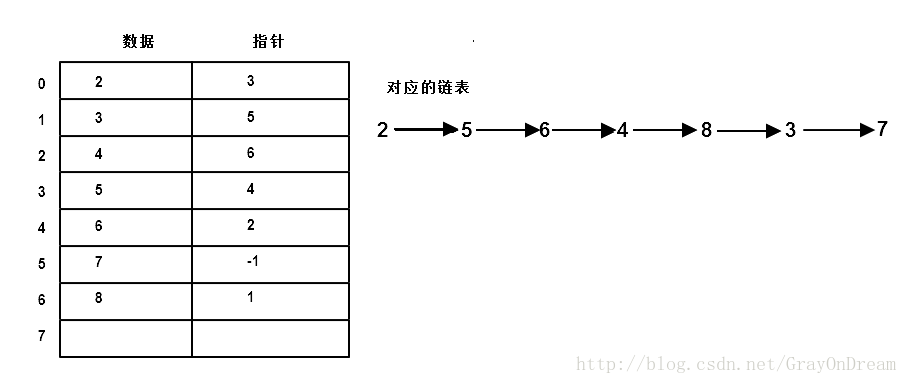
}ListNode, *LinkList;另外还要提一个不太常用的静态链表,适用于没有指针支持的语言中,用线性表存储链表的元素,同样维护一个数据域和一个指针域,只不过这里的指针域并不是真的指针而是数组的下标,用数组下标来连接结点之间的关系。-1表示链表的尾结点。删除和插入操作和一般的链表相同,不同的地方是个人自定义的静态量表的方式不同可能对代码的影响不小。
结构定义为:
#define MAX_SIZE 100
typedef int ElemType;
typedef struct
{
ElemType data;
int next;
}SLinkList[MAX_SIZE];三、相关操作的代码实现
1、顺序表插入操作
插入操作就是将某个元素插入到线性表的指定位置,算法描述:如果需要将元素插入到i处,当i不合法即在0
//function: insert a element into the position of 'i'
//parameters: L a pointer which points to the list
// i the position you would insert
// e the element you would insert
//return: FALSE insert failed
// TRUE insert successfully
int ListInsert(sqList* L, int index ,ElemType e)
{
int i = 0;
if(index < 0 || index > L->length + 1|| L->length == MAX_SIZE)
{
return FALSE;
}
for(i = L->length; i >= index; i --)
{
L->data[i] = L->data[i - 1];
}
L->data[index - 1] = e;
L->length ++;
return TRUE;
}动态内存分配的插入实现
//function: insert a element into the position of 'i'
//parameters: L a pointer which points to the list
// i the position you would insert
// e the element you would insert
//return: FALSE insert failed
// TRUE insert successfully
int ListInsert(sqList* L, int index ,ElemType e)
{
int i = 0;
ElemType* ptr = NULL;
if(index < 0 || index > L->length + 1)
{
return FALSE;
}
if(L->length == L->maxSize)
{
ptr = (ElemType*)realloc(L->data, sizeof(ElemType) * (L->maxSize + INCREASE_SIZE));
if(NULL == ptr)
{
return FALSE;
}
L->data = ptr;
L->maxSize = L->maxSize + INCREASE_SIZE;
}
for(i = L->length; i >= index; i --)
{
L->data[i] = L->data[i - 1];
}
L->data[index - 1] = e;
L->length ++;
return TRUE;
}2、顺序表删除操作
删除操作和插入操作几乎相反,算法描述:如果需要删除第i个元素,直接将该元素后的所有元素前移一位即可。时间复杂度为O(n)。
假如有个a[12]的顺序线性表,想要删除第四个元素:
顺序表删除的实现
//function: delete a element from the list
//parameters: L a pointer which points to the list
// i the position of the element you would delete
// e a pointer which would save the element you would delete
//return: FALSE delete failed
// TRUE delete successfully
int ListDelete(sqList* L, int index, ElemType* e)
{
int i = 0;
if(index > L->length || index < 0)
{
return FALSE;
}
*e = L->data[index - 1];
for(i = index - 1; i < L->length - 1; i ++)
{
L->data[i] = L->data[i + 1];
}
L->length --;
return TRUE;
}3、链表的插入
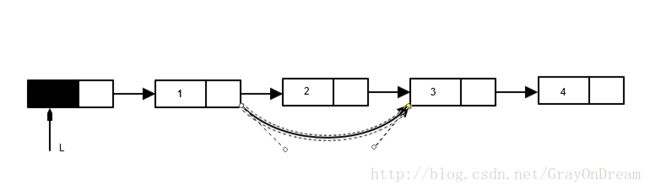
单链表的插入相对来说比较简单,就是修改指针,假如要将s插入到p的后面进行的操作时间复杂度为O(1)
s->next = p->next;
p->next = s;双链表的插入操作相对来说要复杂一点,但是执行原理相同,假如将s插入到p的后面:
s->next = p->next;
p->next->prior = s;
p->next = s;
s->prior = p;具体实现代码
//function: insert a element into the position of 'i'
//parameters: L a pointer which points to the list
// i the position you would insert
// e the element you would insert
//return FALSE insert failed
// TRUE insert successfully
int ListInsert(LinkList* L, int index ,ElemType e)
{
int i = 0;
LinkList ptr = NULL;
LinkList tmp = NULL;
if(NULL == (*L) || index < 0 || index > (*L)->data + 1)
{
return FALSE;
}
ptr = (*L);
for(i = 0;i < index - 1;i ++)
{
ptr = ptr->next;
}
tmp = (LinkList)malloc(sizeof(LinkNode));
if(tmp == NULL)
{
return FALSE;
}
tmp->data = e;
tmp->next = ptr->next;
ptr->next = tmp;
(*L)->data ++;
return TRUE;
}//ListInsert4、链表的删除
链表的删除操作直接跳过要删除的结点时间复杂度为O(1)即可:
p->next = s->next;
free(s);双链表的删除基本相似,若要删除p后的s结点:
s->next->prior = p;
p->next = s->next;
free(s);具体实现代码
//function: delete a element from the list
//parameters: L a pointer which points to the list
// i the position of the element you would delete
// e a pointer which would save the element you would delete
//return: FALSE delete failed
// TRUE delete successfully
int ListDelete(LinkList* L, int index, ElemType* e)
{
int i = 0;
LinkList ptr = (*L);
LinkList tmp = NULL;
if(NULL == (*L) || index > (*L)->data || index < 1)
{
return FALSE;
}
for(i = 0;i < index - 1;i ++)
{
ptr = ptr->next;
}
tmp = ptr->next;
ptr->next = tmp->next;
free(tmp);
tmp = NULL;
(*L)->data--;
return TRUE;
}//ListDelete相关代码的链接:http://download.csdn.net/detail/grayondream/9731257