【算法】图解+变式——带你彻底搞懂字典树(Trie树)
啥是字典树?
【字典树】(Trie Tree) 是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串)。
它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
——百度 · 百科
so?所以到底什么是字典树?
还好,它还有其他的名字,更能表述出它的实质:
前缀树、单词查找树
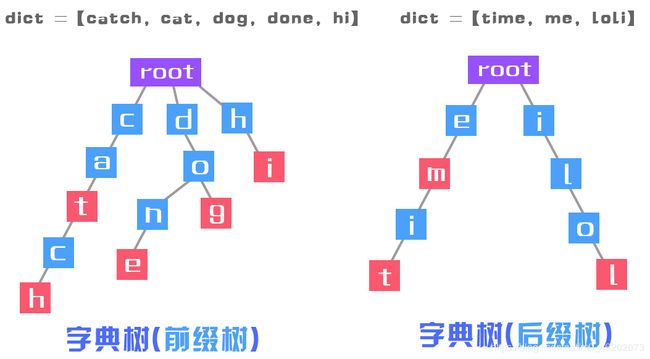
直接看图吧——更直观的理解它名字的由来。何谓前缀?何谓单词查找?
下面,进入正题。
接下来将对经典的字典树进行代码实现;接着做几个变体题目深入理解字典树的强大;最后回到日常生活,瞧瞧字典树怎样融入到了我们的生活之中 >_<
▊ 经典的字典树(只包含26个小写字母)
首先,数据结构嘛,肯定是要先构建节点(Node);
弄清了节点的结构和含义,一棵树(Tree)的构建就会水到渠成
class TrieNode {
boolean isWord; // 从root根节点至此是否是一个完整的单词(即这个节点是否是一个单词的结尾)
TrieNode[] children = new TrieNode[26]; // 巧妙的用数组的下标作为26个字母;数组的值则为子节点
public TrieNode(){} // 打酱油的无参构造函数(不写也行)
}
class TrieNode { // 最标准写法
boolean isWord;
TrieNode[] children;
public TrieNode {
isWord = false;
children = new TrieNode[26];
}
}
这里有两个关键点:
- isWord为true的节点就是上面的图中红色的节点。举个例子,两个字符串"cat"和"catch",字符
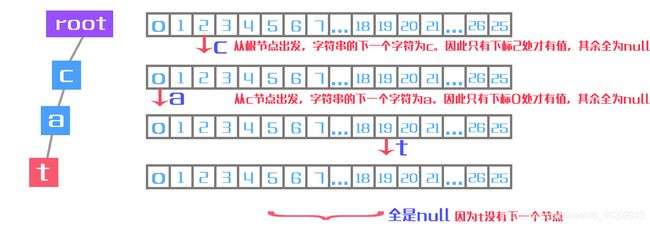
t和字符h对应的节点,就是红色的(isWord = true) - 第二点很巧妙:利用了一个长度为26的TrieNode[]数组,用下标表示字符(
char - 'a'),用该下标对应的值表示指向子节点的引用(看下面的图 ! ! !)。例如字符串"cat",根节点有26个"触手",只有c对应的那个下标(‘c’ - ‘a’ = 2)才是有值的,其余的全为null,表示这条路走不通。另外,如果没有a-z的限制,就不能用数组,而使用哈希表。
构建好了节点,下面开始构建树,并写出树的一些方法 ↓
class TrieNode { // 节点
boolean isWord;
TrieNode[] children = new TrieNode[26];
}
class Trie {
TrieNode root; // 根节点
public Trie() {
root = new TrieNode(); // 构造字典树,就是先构造出一个空的根节点
}
//【向字典树插入单词word】
// 思路:按照word的字符,从根节点开始,一直向下走:
// 如果遇到null,就new出新节点;如果节点已经存在,cur顺着往下走就可以
public void insert(String word) {
TrieNode cur = root; // 先指向根节点
for (int i = 0; i < word.length(); i++) { // 如果是【后缀树】而不是【前缀树】,把单词倒着插就可以了,即for(len-1; 0; i--)
int c = word.charAt(i) - 'a'; // (关键) 将一个字符用数字表示出来,并作为下标
if (cur.children[c] == null) {
cur.children[c] = new TrieNode();
}
cur = cur.children[c];
}
cur.isWord = true; // 一个单词插入完毕,此时cur指向的节点即为一个单词的结尾
}
//【判断一个单词word是否完整存在于字典树中】
// 思路:cur从根节点开始,按照word的字符一直尝试向下走:
// 如果走到了null,说明这个word不是前缀树的任何一条路径,返回false;
// 如果按照word顺利的走完,就要判断此时cur是否为单词尾端:如果是,返回true;如果不是,说明word仅仅是一个前缀,并不完整,返回false
public boolean search(String word) {
TrieNode cur = root;
for (int i = 0; i < word.length(); i++) {
int c = word.charAt(i) - 'a';
if (cur.children[c] == null) {
return false;
}
cur = cur.children[c];
}
return cur.isWord;
}
//【判断一个单词word是否是字典树中的前缀】
// 思路:和sesrch方法一样,根据word从根节点开始一直尝试向下走:
// 如果遇到null了,说明这个word不是前缀树的任何一条路径,返回false;
// 如果安全走完了,直接返回true就行了———我们并不关心此事cur是不是末尾(isWord)
public boolean startsWith(String word) {
TrieNode cur = root;
for (int i = 0; i < word.length(); i++) {
int c = word.charAt(i) - 'a';
if (cur.children[c] == null) {
return false;
}
cur = cur.children[c];
}
return true;
}
}
>>> test
Trie trie = new Trie();
trie.insert("apple");
>>> trie.search("apple") 返回true
>>> trie.search("app") 返回false
>>> trie.startWith("app") 返回true
▊ 变式题目
变式1:利用字典树的构造过程——忽略后缀单词
【Leetcode_820】单词的压缩
给定一个单词列表,我们将这个列表编码成一个索引字符串 S 与一个索引列表 A。
例如,如果这个列表是 [“time”, “me”, “bell”],我们就可以将其表示为 S = “time#bell#” 和 indexes = [0, 2, 5]。# 表示一个结束位置
那么成功对给定单词列表进行编码的最小字符串长度是多少呢?
示例:
输入: words = [“time”, “me”, “bell”]
输出: 10
说明: 字符串S = “time#bell#” ,
提示: 1 <= words.length <= 2000 1 <= words[i].length <= 7 每个单词都是小写字母 。
class Solution_820 {
/*
【字典树】——— 之所以想到使用字典树,是因为该题完全发挥了字符串的后缀特征
我们构造出这样的一个[逆序]字典树,很容易发现: "编码"后的字符串长度,就是忽略了后缀单词后,所有单词的(长度+1)之和
这不难理解,比如"abcd#","bcd","cd","d"这种后缀单词就默认被包括了,因而算整个字符串的长度时,算"abcd"这个最长的就行了
核心思路是:每次往字典树插入一个"新的word"时,就 += 该word的长度 + 1(#)
需要注意的是,不是每一次插入单词,都需要加上该单词的长度
而是先根据长度对words进行一次排序,先插入长的,再插入短的。如果插入时需要new出新节点,我们就认为这是一个"新word"
举几个例子:
1. 先插"cba",再插"dba" ———— 虽然后缀有重合,但是依旧需要new出新节点,认为是"新word",最终字符串只能为"cba#dba#"
2. 先插"ba",再插"dcba" ———— 两次插入都有new出新节点的行为,因此算多了,3+1 + 5+1 =8,实际为"dcba#",为5
3. 先插"dcba",再插"ba" ———— 因为先插长的,第二次插入并没有出现new的行为,4+1 = 5,正确 ! ! !
*/
public int minimumLengthEncoding(String[] words) {
int resLen = 0;
Arrays.sort(words, (s1, s2) -> s2.length() - s1.length());
Trie trie = new Trie();
for(String word : words){
resLen += trie.insert(word);
}
return resLen;
}
}
class TrieNode {
boolean isWord;
TrieNode[] children = new TrieNode[26];
TrieNode() {
}
}
class Trie {
TrieNode root;
public Trie() {
root = new TrieNode();
}
// 单词逆序插入字典树;插入的同时,还会判断插入的单词是不是"新的",如果是新单词,返回其length+1;否则返回0
public int insert(String word) {
TrieNode cur = root;
boolean isNew = false;
for (int i = word.length() - 1; i >= 0; i--){
int c = word.charAt(i) - 'a';
if(cur.children[c] == null){
cur.children[c] = new TrieNode();
isNew = true; // 如果出现new出新节点的行为,则认为是"新word"
}
cur = cur.children[c];
}
cur.isWord = true;
return isNew? word.length() + 1 : 0;
}
}
变式2:利用字典树充分利用前缀(后缀)性质,优化暴力算法
【Leetcode_面试题_17_13】恢复空格
哦,不!你不小心把一个长篇文章中的空格、标点都删掉了,并且大写也弄成了小写。像句子"I reset the computer. It still didn’t boot!“已经变成了"iresetthecomputeritstilldidntboot”。在处理标点符号和大小写之前,你得先把它断成词语。当然了,你有一本厚厚的词典dictionary,不过,有些词没在词典里。假设文章用sentence表示,设计一个算法,把文章断开,要求未识别的字符最少,返回未识别的字符数。
注意:本题相对原题稍作改动,只需返回未识别的字符数
示例:
输入: dictionary = [“looked”,“just”,“like”,“her”,“brother”] sentence = “jesslookedjustliketimherbrother”
输出: 7
解释: 断句后为"jess looked just like tim her brother",共7个未识别字符。
提示:只包含26个小写字母
class Solution_17_13_2 {
/*
【动态规划 + 字典树】
我们发现,在给dp[i]填值时,需要切割出所有以 i-1 处字符为结尾的子串———这导致了O(n²)的复杂度
但实际上,当某个后缀已经不存在时,就没有再继续切割的必要了
比如"abcdef",给dp[4]填值时("前4个字符的最少未被匹配字符数"),发现已经不存在以"cd"为后缀的word,那么就不用继续切割出"bcd","abcd"了
因此我们使用【字典树】,对这一点进行优化————
不是切割出所有子串然后判断,而是根据字典树从i-1处的字符开始,尝试扩大这个后缀串,并返回所有可能作为word开头的坐标;直接根据找的坐标更新dp
*/
public int respace(String[] dictionary, String sentence) {
int len = sentence.length();
int[] dp = new int[len + 1];
Trie trie = new Trie();
for(String word : dictionary){
trie.insert(word);
}
// 动态规划
for(int i = 1; i <= len; i++){
dp[i] = dp[i - 1] + 1;
for(int j : trie.search(sentence, i - 1)){ // 前i个字符,结尾单词的下标是 i - 1
dp[i] = Math.min(dp[i], dp[j]);
}
}
return dp[len];
}
}
class TrieNode{
boolean isWord;
TrieNode[] children = new TrieNode[26];
public TrieNode() {}
}
class Trie{
TrieNode root; // 根节点
public Trie(){
root = new TrieNode();
}
// 单词word插入字典树(逆序) 【模板】
public void insert(String word){
TrieNode cur = root;
for(int i = word.length() - 1; i >= 0; i--){
int c = word.charAt(i) - 'a';
if(cur.children[c] == null){
cur.children[c] = new TrieNode();
}
cur = cur.children[c];
}
cur.isWord = true;
}
// 找到 sentence 中以 sentence[end] 为结尾的单词(可能不止一个),返回这些单词的开头下标 【★关键】
public List<Integer> search(String sentence, int end){
List<Integer> resList = new ArrayList<>();
TrieNode cur = root;
for(int i = end; i >= 0; i--){
int c = sentence.charAt(i) - 'a';
if(cur.children[c] == null){ // 从结尾处开始,一直尝试向前找,如果发现后缀已经不合法,直接终止
break; // 这两行就是字典树对原算法的优化
}
cur = cur.children[c];
if(cur.isWord){
resList.add(i);
}
}
return resList;
}
}
变式3:search方法的变异——match递归
>>> 经典的search方法,是通过一个cur指针(引用),根据word的字符,一条路走下去
>>> 其实,它还有一个思路———每次判断一个节点是否配对 的【递归】写法 :
public boolean search(String word) {
return match(word, root, 0);
}
/* macth方法
// 基本思路是:根据word和start得到此时的字符,然后看该字符是否与此时的节点node配对————即node.children[c]有值(!=null)
// (其实start就相当于非递归写法中的for(i)的i),用来遍历word
*/
public boolean match(String word, TrieNode node, int start){ // 这个三个参数直接背下来,这是模板参数
if(start == word.length()){
return node.isWord; // (★)
}
int c = word.charAt(start) - 'a';
return node.children[c] != null && match(word, node.children[c], start + 1);
}
Q:我知道match递归写法很妙,但有什么用呢?cur一条路走到黑的思路不是更好理解吗?
A:恰恰是因为“cur一条路走到黑”的思路有弊端——有时我们需要走一个分叉的路,去尝试更多的可能。
通过下面的两道变式题目,就能理解递归型search的强大之处
变式4:含有通配符的字典树匹配——递归的search
【Leetcode_211】添加与搜索单词-数据结构设计
设计一个支持以下两种操作的数据结构:void addWord(word) 添加单词
bool search(word) 可以搜索文字或正则表达式字符串,字符串只包含字母 . 或 a-z 。 ‘.’ 可以表示任何一个字母。
// TrieNode节点代码省略
class WordDictionary {
TrieNode root;
public WordDictionary() {
root = new TrieNode();
}
public void addWord(String word) { // 你应该非常熟悉这个insert/addWord方法了吧!
TrieNode cur = root;
for(int i = 0; i < word.length(); i++){
int c = word.charAt(i) - 'a';
if(cur.children[c] == null){
cur.children[c] = new TrieNode();
}
cur = cur.children[c];
}
cur.isWord = true;
}
public boolean search(String word) {
return match(word, root, 0);
}
public boolean match(String word, TrieNode node, int start){
if(start == word.length()) {
return node.isWord; // 3个参数和这个终止条件是比较固定的模板
}
if(word.charAt(start) != '.') { // 不是通配符,还是原先的递归写法
int c = word.charAt(start) - 'a';
return node.children[i] != null && match(word, node.children[c], start + 1);
}else { // 是通配符,对26中可能进行递归
for(int i = 0; i < 26; i++){
if(node.children[i] != null && match(word, node.children[i], start + 1)){
return true;
}
}
return false;
}
}
变式5:允许且必须变化一个字符后再匹配——递归的search
【Leetcode_676】实现一个魔法字典
实现一个带有buildDict, 以及 search方法的魔法字典。
对于buildDict方法,你将被给定一串不重复的单词来构建一个字典。
对于search方法,你将被给定一个单词,并且判定能否只将这个单词中一个字母换成另一个字母,使得所形成的新单词存在于你构建的字典中。
>>> 你会遇到一个棘手的问题,就是当字典树中有"hello"和"hallo"时,search("hello")会返回false。
问题的关键在于:一般我们写search,都是根据word先算出下标————这会导致,字典树从hello这条路,一路走到头,因为没有修改任何一个字母导致返回false。
因此,千万要抛弃这个字典树的search模板,改为一次for(26)的遍历。
>>> 逻辑是:
发现这个字母可行后,再去看这个"可行的字母"是不是就是"word.charAt(start)"
而不是根据"word.charAt(start)",看这个字母是否"可行" (可行的意思是,这是字典树的一个合法节点)
理解上面这句话,是解决第一行那个问题的关键。
// TrieNode节点代码省略
class MagicDictionary {
TrieNode root;
public MagicDictionary() {
root = new TrieNode();
}
// 构建字典树的代码省略了
public boolean search(String word) {
return match(word, root, 0, true);
}
/*
* 这个递归本身是极其简练、优美的 (两个if)
*/
public boolean match(String word, TrieNode node, int start, boolean hasChance){
if(start == word.length()){
return node.isWord && !hasChance; // 因为"必须变一个字符",因此 "&& !hasChance"
}
for(int i = 0; i < 26; i++){
if(node.children[i] != null){
if(word.charAt(start)-'a' == i && match(word, node.children[i], start + 1, hasChance)){
return true;
}
if(word.charAt(start)-'a' != i && hasChance && match(word, node.children[i], start + 1, false)){
return true;
}
}
}
return false;
}
}
▊ Trie树与日常生活(烧脑终于结束啦!)
字典树(前缀树后缀树,单词查找树)其实早已融入了我们生活的点滴之中 :
自动补全(输入法也是哦)
敏感词检测
面试/考试的时候很喜欢问一些关于搜索引擎的问题。这是一个经典问题,搜索引擎如何判断你搜索的内容是敏感词?
哦,我知道!是建立一个敏感词组成的Hash集合,将搜索内容利用分词库进行分词,分出的词去进行Hash匹配。
你获得了30分。
Hash的方法并不准确——“我爱日本”,分词出“我”,“爱”,“日本”,每个切片都毫无问题,组合在一起呢?
Hash的方法代价太高——为了解决上面的问题,只能把“我爱日本”作为一个整体加入哈希集合中。但是,你又需要把"我爱Japan",“我爱JAPAN”,“我love日本”,"我love Japan"这样各种组合加入哈希集合,开销不可想象。
因此,海量敏感词的存储方式必然不是Hash,而是一个多叉的树形结构(比如Trie树)
☑ 部分题目来源 :
【Leetcode Q208 】实现Trie (前缀树)
【 Leetcode Q820 】单词的压缩编码
【 Leetcode Q17_13 】恢复空格
【 Leetcode Q211】 添加与搜索单词-数据结构设计
【 Leetcode Q676 】实现一个魔法字典
结束了,不知道你意识到没有,Trie树的检索机制,和你的《英语词典》完全一致。
这是我想说的最后一个问题的答案——"字典树"名称的由来。
♬ END
♪ By a Lolicon ♥