20200802:力扣200周周赛题解
第200周周赛题解
第一题:统计好三元组
给你一个整数数组 arr ,以及 a、b 、c 三个整数。请你统计其中好三元组的数量。
如果三元组 (arr[i], arr[j], arr[k]) 满足下列全部条件,则认为它是一个 好三元组 。
-
0 <= i < j < k < arr.length
-
|arr[i] - arr[j]| <= a
-
|arr[j] - arr[k]| <= b
-
|arr[i] - arr[k]| <= c
-
其中 |x| 表示 x 的绝对值。
返回 好三元组的数量 。
示例
输入:arr = [3,0,1,1,9,7], a = 7, b = 2, c = 3
输出:4
解释:一共有 4 个好三元组:[(3,0,1), (3,0,1), (3,1,1), (0,1,1)] 。
输入:arr = [1,1,2,2,3], a = 0, b = 0, c = 1
输出:0
解释:不存在满足所有条件的三元组。
解题思路与代码实现:
直接暴力即可
class Solution {
public int countGoodTriplets(int[] arr, int a, int b, int c) {
int ans = 0;
for (int i = 0; i < arr.length - 2; i++) {
for (int j = i + 1; j < arr.length - 1; j++) {
for (int k = j + 1; k < arr.length; k++) {
if (Math.abs(arr[i] - arr[j]) <= a && Math.abs(arr[j] - arr[k]) <= b && Math.abs(arr[i] - arr[k]) <= c) {
ans++;
}
}
}
}
return ans;
}
}
第二题:找出数组游戏的赢家
给你一个由 不同 整数组成的整数数组 arr 和一个整数 k 。
每回合游戏都在数组的前两个元素(即 arr[0] 和 arr[1] )之间进行。比较 arr[0] 与 arr[1] 的大小,较大的整数将会取得这一回合的胜利并保留在位置 0 ,较小的整数移至数组的末尾。当一个整数赢得 k 个连续回合时,游戏结束,该整数就是比赛的 赢家 。
返回赢得比赛的整数。
题目数据 保证 游戏存在赢家。
示例
输入:arr = [2,1,3,5,4,6,7], k = 2
输出:5
解释:一起看一下本场游戏每回合的情况:

因此将进行 4 回合比赛,其中 5 是赢家,因为它连胜 2 回合。
解题思路及代码实现
本题一上来的思路是模拟整个移动过程,每次记录当前winner及其连胜次数,但是仔细观察后发现不需要那么复杂,换个思路来讲,本题的意思就是打擂台,连胜场次到达k次后即可获胜,返回擂主。题目要求擂主永远在1号擂台,我们转换思路让擂主逐一挑战各擂台,从1号开始扫荡后续所有擂台,统计其连胜场次即可。
class Solution {
public int getWinner(int[] arr, int k) {
// 1号擂主
int ans = arr[0];
int count = 0;
for (int i = 1; i < arr.length; i++) {
// 擂主易主,注意易主的时候擂主已经获得1胜,别设置为0了
if (arr[i] > ans) {
count = 1;
ans = arr[i];
} else {
// 连胜则统计次数
count++;
}
// 判断当前连胜次数是否已经达标
if (count >= k) {
break;
}
}
return ans;
}
}
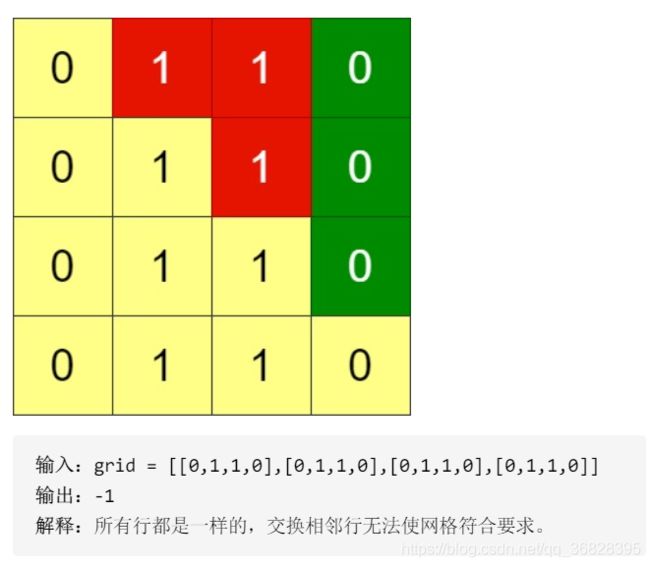
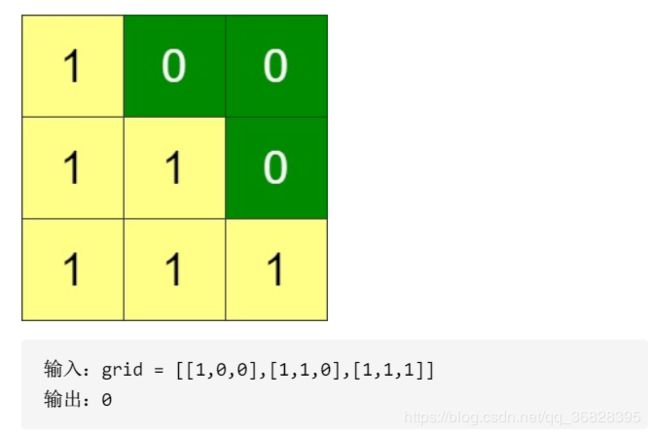
第三题:排布二进制网格的最少交换次数
给你一个 n x n 的二进制网格 grid,每一次操作中,你可以选择网格的 相邻两行 进行交换。
一个符合要求的网格需要满足主对角线以上的格子全部都是 0 。
请你返回使网格满足要求的最少操作次数,如果无法使网格符合要求,请你返回 -1 。
主对角线指的是从 (1, 1) 到 (n, n) 的这些格子。
示例
解题思路与代码实现
本题直接看到每一行的末尾的连续0的个数与当前所在行行数的关系,比如矩阵为3X3,我在第1行,那么第一行需要末尾3-1 = 2个0,第二行3-2 = 1个0,第三行3-3=0个不需要。那么我们只需要判断每一行的末尾连续0的个数,然后对应判断需要换行多少次计入count即可。如果不符合要求,则按照题目要求返回 -1。具体见代码
class Solution {
public int minSwaps(int[][] grid) {
int ans = 0;
int[] arr = new int[grid.length];
for (int i = 0; i < grid.length; i++) {
arr[i] = getSeriousZeros(grid[i]);
}
// 此时判断arr[i]与len-1-i的关系即可
for (int i = 0; i < arr.length; i++) {
boolean flag = false;
for (int j = i;j < arr.length; j++) {
if (arr[j] >= arr.length - i - 1 && !flag) {
ans += swapCount(arr,i,j);
flag = true;
}
}
if (!flag) {
return -1;
}
}
return ans;
}
private static int swapCount(int[] arr,int i,int j) {
int ans = 0;
while (i < j) {
int tmp = arr[j - 1];
arr[j - 1] = arr[j];
arr[j] = tmp;
ans++;
j--;
}
return ans;
}
private static int getSeriousZeros(int[] arr){
int ans = 0;
int len = arr.length;
for (int i = len - 1; i >= 0; i--) {
if (arr[i] == 0) {
ans++;
} else {
break;
}
}
return ans;
}
}
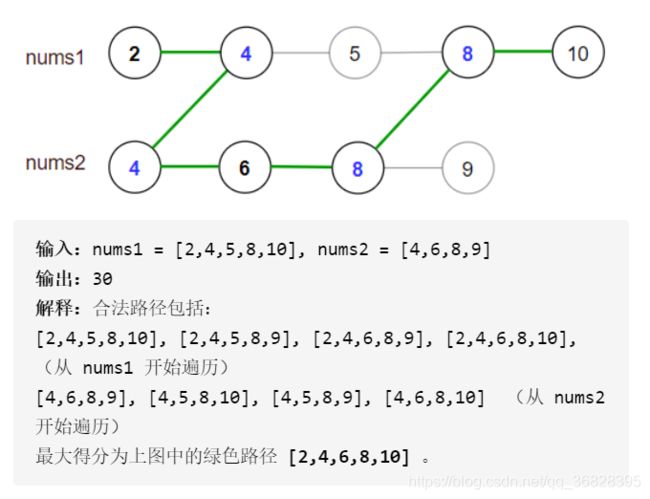
第四题: 最大得分
你有两个 有序 且数组内元素互不相同的数组 nums1 和 nums2 。
一条 合法路径 定义如下:
-
选择数组 nums1 或者 nums2 开始遍历(从下标 0 处开始)。
-
从左到右遍历当前数组。
-
如果你遇到了 nums1 和 nums2 中都存在的值,那么你可以切换路径到另一个数组对应数字处继续遍历(但在 合法路径中重复数字只会被统计一次)。
-
得分定义为合法路径中不同数字的和。
请你返回所有可能合法路径中的最大得分。
由于答案可能很大,请你将它对 10^9 + 7 取余后返回。
示例
解题思路与代码实现
本周赛压轴题,直接模拟即可,没有太多思路障碍,注意书写即可
class Solution {
public int maxSum(int[] nums1, int[] nums2) {
int MOD = 1000000007;
long ans1 = 0,ans2 = 0;
int len1 = nums1.length,len2 = nums2.length;
int i = 0,j = 0;
// 从两个数组开始的和
while (i < len1 && j < len2) {
if (nums1[i] < nums2[j]) {
ans1 += nums1[i];
i++;
} else if (nums1[i] > nums2[j]) {
ans2 += nums2[j];
j++;
} else {
ans1 = Math.max(ans1,ans2) + nums1[i];
ans2 = ans1;
i++;
j++;
}
}
// 剩下的加起来
while (i < len1) {
ans1 += nums1[i];
i++;
}
while (j < len2) {
ans2 += nums2[j];
j++;
}
return (int) (Math.max(ans1,ans2) % MOD);
}
}