视觉笔记 - 视觉坐标系
by luoshi006
参考:张正友
参考:相机成像原理 - 陈建平
视觉坐标系
图像坐标系
像素(pixel)
像素是数字图像中最小的点(单位色块),其值表示图像点的亮度(灰度)。像素的大小是没有固定长度值的,不同设备上1个单位像素色块的大小是不一样的。
数字图像
相机获取的图像在计算机内以 M × N M \times N M×N 数组的形式存储,数组中的元素为像素。
像素坐标系
如图所示,在图像上定义坐标系 u - v u\text{-}v u-v,每个像素坐标 ( u , v ) (u,v) (u,v) 分别是该像素在图像中的列数和行数,即,得到以像素为单位的坐标 ( u , v ) (u,v) (u,v)。
图像坐标系
也就是 成像平面坐标系,在焦距 f f f 处的平面。
建立以 SI 单位(米)表示的图像坐标系 x - y x\text{-}y x-y,该坐标系以 o ( u 0 , v 0 ) o(u_0,v_0) o(u0,v0) 为原点, x x x 轴、 y y y 轴分别与 u u u 轴、 v v v 轴平行, ( x , y ) (x,y) (x,y) 表示以物理单位度量的图像坐标。在 x - y x\text{-}y x-y 坐标系中,原点 o o o 定义为相机光轴和成像平面的交点,一般位于图像中心处,称为图像的主点。
原点 o ( u 0 , v 0 ) o(u_0,v_0) o(u0,v0) 在 u - v u\text{-}v u-v 坐标系中的坐标为 ( u 0 , v 0 ) (u_0,v_0) (u0,v0),每个像素在 x x x 轴和 y y y 轴方向上的物理尺寸为 d x , d y dx, dy dx,dy。

相机坐标系
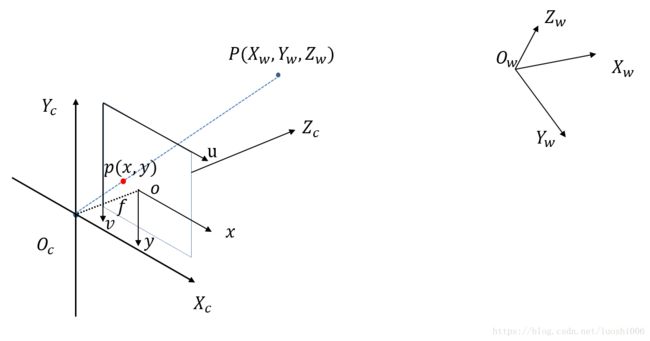
成像模型是指 3D 点到像平面的投影关系。在小孔成像模型中,3D 点 P P P 投影到像平面上的像点 p p p,其中, O c O_c Oc 为相机光心; X c 、 Y c X_c、Y_c Xc、Yc 轴分别与图像坐标系的 x 、 y x、y x、y 轴平行; Z c Z_c Zc 为相机的光轴,与像平面垂直,相交于点 o o o; f f f 为相机焦距;相机坐标系记为: O c - X c Y c Z c O_c \text{-} X_cY_cZ_c Oc-XcYcZc。

世界坐标系
相机可安放在场景中的任意位置,所以,在场景中选择一个基准坐标系来描述相机的位姿,以及场景中任何物体的位置(3D 点),该坐标系称为世界坐标系,记为 O w - X w Y w Z w O_w \text{-} X_wY_wZ_w Ow-XwYwZw。
视觉坐标系变换
世界坐标系 与 相机坐标系
相机坐标系和世界坐标系的关系用旋转矩阵 R R R 与平移向量 t t t 来描述。
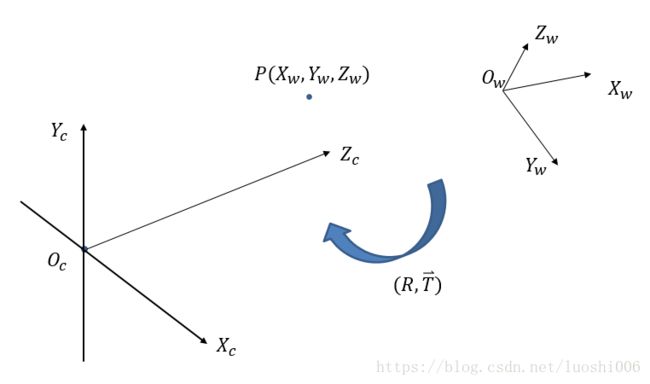
[ X c Y c Z c ] = R [ X w Y w Z w ] + t \begin{bmatrix}X_c\\Y_c\\Z_c \end{bmatrix}= R\begin{bmatrix}X_w\\Y_w\\Z_w \end{bmatrix}+t ⎣⎡XcYcZc⎦⎤=R⎣⎡XwYwZw⎦⎤+t
[ X c Y c Z c 1 ] = [ R t 0 ⃗ 1 ] [ X w Y w Z w 1 ] \begin{bmatrix}X_c\\Y_c\\Z_c\\1 \end{bmatrix}= \begin{bmatrix}R & t\\ \vec 0&1 \end{bmatrix} \begin{bmatrix}X_w\\Y_w\\Z_w\\1 \end{bmatrix} ⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤=[R0t1]⎣⎢⎢⎡XwYwZw1⎦⎥⎥⎤
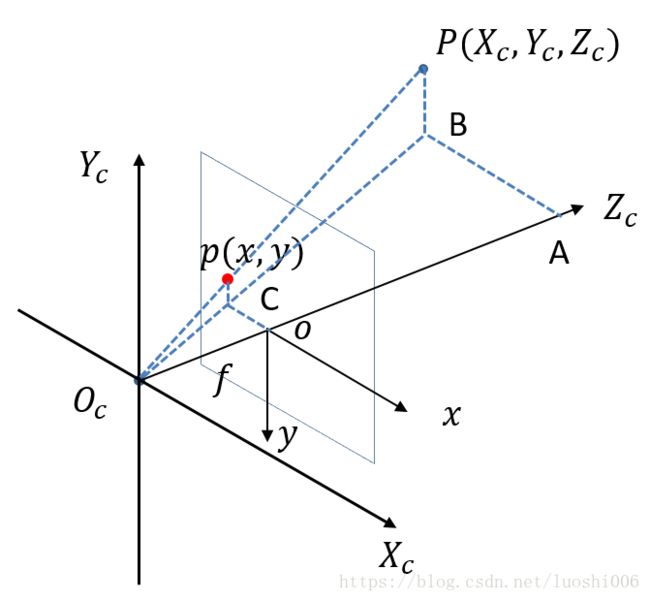
相机坐标系 与 图像坐标系
从小孔成像模型中,可以看出相机坐标系与成像平面坐标系之间的相似变换关系:
x = f X c Z c , y = f Y c Z c x = f \frac{X_c}{Z_c}, y = f \frac{Y_c}{Z_c} x=fZcXc,y=fZcYc
整理得:
Z c [ x y 1 ] = [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ X c Y c Z c 1 ] Z_c\begin{bmatrix}x\\y\\1 \end{bmatrix}= \begin{bmatrix}f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix}X_c\\Y_c\\Z_c\\1 \end{bmatrix} Zc⎣⎡xy1⎦⎤=⎣⎡f000f0001000⎦⎤⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤
图像坐标系 与 像素坐标系

{ u = x d x + u 0 v = y d y + v 0 \left \{\begin{aligned} u = \frac{x}{dx}+u_0\\ v = \frac{y}{dy}+v_0 \end{aligned} \right . ⎩⎪⎨⎪⎧u=dxx+u0v=dyy+v0
整理得(齐次坐标):
[ u v 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ x y 1 ] \begin{bmatrix} u \\v \\1 \end{bmatrix} = \begin{bmatrix} \frac{1}{dx} & 0 & u_0 \\ 0 & \frac{1}{dy} & v_0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\y \\1 \end{bmatrix} ⎣⎡uv1⎦⎤=⎣⎡dx1000dy10u0v01⎦⎤⎣⎡xy1⎦⎤
逆变换为(齐次坐标):
[ x y 1 ] = [ d x 0 − u 0 ⋅ d x 0 d y − v 0 ⋅ d y 0 0 1 ] [ u v 1 ] \begin{bmatrix} x \\y \\1 \end{bmatrix} = \begin{bmatrix}{dx} & 0 & -u_0 \cdot dx \\ 0 & {dy} & -v_0 \cdot dy \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix}u \\v \\1 \end{bmatrix} ⎣⎡xy1⎦⎤=⎣⎡dx000dy0−u0⋅dx−v0⋅dy1⎦⎤⎣⎡uv1⎦⎤
像素坐标系 与 相机坐标系 [x]
已知相机内参矩阵 K K K:
Z c [ u v 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ X c Y c Z c 1 ] = K [ X c Y c Z c 1 ] \begin{aligned} Z_c\begin{bmatrix}u\\v\\1\\ \end{bmatrix} &= \begin{bmatrix}\frac{1}{dx} & 0 & u_0\\ 0 & \frac{1}{dy} & v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix}X_c\\Y_c\\Z_c\\1\end{bmatrix} \\ & = K\begin{bmatrix}X_c\\Y_c\\Z_c\\1\end{bmatrix} \end{aligned} Zc⎣⎡uv1⎦⎤=⎣⎡dx1000dy10u0v01⎦⎤⎣⎡f000f0001000⎦⎤⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤=K⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤
世界坐标系 与 像素坐标系

Z c [ u v 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ x y 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ X c Y c Z c 1 ] = [ 1 d x 0 u 0 0 1 d y v 0 0 0 1 ] [ f 0 0 0 0 f 0 0 0 0 1 0 ] [ R t 0 ⃗ 1 ] [ X w Y w Z w 1 ] = [ f x 0 u 0 0 0 f y v 0 0 0 0 1 0 ] ⎵ 相机内参 [ R t 0 ⃗ 1 ] ⎵ 相机外参 [ X w Y w Z w 1 ] \begin{aligned} Z_c\begin{bmatrix}u\\v\\1\\ \end{bmatrix} &= \begin{bmatrix}\frac{1}{dx} & 0 & u_0\\ 0 & \frac{1}{dy} & v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}x\\y\\1\\\end{bmatrix}\\ &= \begin{bmatrix}\frac{1}{dx} & 0 & u_0\\ 0 & \frac{1}{dy} & v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix}X_c\\Y_c\\Z_c\\1 \end{bmatrix}\\ &= \begin{bmatrix}\frac{1}{dx} & 0 & u_0\\ 0 & \frac{1}{dy} & v_0\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}f & 0 & 0 & 0\\ 0 & f & 0 & 0\\ 0 & 0 & 1 & 0 \end{bmatrix} \begin{bmatrix}R & t\\ \vec 0&1 \end{bmatrix} \begin{bmatrix}X_w\\Y_w\\Z_w\\1 \end{bmatrix}\\ &= \underbrace{\begin{bmatrix}f_x & 0 & u_0 & 0\\ 0 & f_y & v_0 & 0\\ 0 & 0 & 1 & 0 \end{bmatrix}}_{\textbf{相机内参}} \underbrace{\begin{bmatrix}R & t\\ \vec 0&1 \end{bmatrix}}_{\textbf{相机外参}} \begin{bmatrix}X_w\\Y_w\\Z_w\\1 \end{bmatrix} \end{aligned} Zc⎣⎡uv1⎦⎤=⎣⎡dx1000dy10u0v01⎦⎤⎣⎡xy1⎦⎤=⎣⎡dx1000dy10u0v01⎦⎤⎣⎡f000f0001000⎦⎤⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤=⎣⎡dx1000dy10u0v01⎦⎤⎣⎡f000f0001000⎦⎤[R0t1]⎣⎢⎢⎡XwYwZw1⎦⎥⎥⎤=相机内参 ⎣⎡fx000fy0u0v01000⎦⎤相机外参 [R0t1]⎣⎢⎢⎡XwYwZw1⎦⎥⎥⎤
归一化平面
与像素坐标变换:
[ x 1 y 1 1 ] = K − 1 [ u v 1 ] \begin{bmatrix} x_1\\ y_1\\1 \end{bmatrix}= K^{-1}\begin{bmatrix} u\\ v\\1 \end{bmatrix} ⎣⎡x1y11⎦⎤=K−1⎣⎡uv1⎦⎤
称 [ x 1 y 1 1 ] T \begin{bmatrix} x_1& y_1&1 \end{bmatrix}^T [x1y11]T 为像素平面的归一化坐标。
Note
使用归一化坐标计算时,相当于内参矩阵为单位阵,相机焦距为 1。
Z c [ x 1 y 1 1 ] = [ 1 0 0 0 0 1 0 0 0 0 1 0 ] [ X c Y c Z c 1 ] Z_c \begin{bmatrix} x_1\\ y_1\\1 \end{bmatrix}= \begin{bmatrix} 1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\ \end{bmatrix} \begin{bmatrix} X_c\\ Y_c\\Z_c\\1 \end{bmatrix} Zc⎣⎡x1y11⎦⎤=⎣⎡100010001000⎦⎤⎣⎢⎢⎡XcYcZc1⎦⎥⎥⎤
故:
x 1 = X c Z c , y 1 = Y c Z c x_1 = \frac{X_c}{Z_c}, y_1 = \frac{Y_c}{Z_c} x1=ZcXc,y1=ZcYc